Corum city is the centre of the Corum governorate that is located at the north of Turkey. To analyse the traffic situation in the city, the main intersections were categorized into signalized and non-signalized intersections. This study analysed signalized roundabouts resulting in a total of eight intersections during the summer of 2015. Cameras were also placed on each intersection (numbers according to the size of the intersection) with the aim of defining traffic volume at rush hours. Rush hour periods were divided into three periods, these included mornings, (7:30–9:30) to cover business time in Turkey that starts at 9:00 AM. The second period was between 12:00–14:00 (end of schools), and the third period was between 16:30–18:30 (end of business day). Thus, for each of these intersections six hours of traffic video were recorded.

The recorded data for each intersection yielded vehicle counts and speeds of 6-types of vehicles: automobile, taxi, minibus, van, bus and heavy trucks. The analysis time of the recorded data was 54 h. Fig. 1 shows the 6th signalized roundabout as a satellite photo. It shows the location of the leg recorder. Table 1 shows a sample of traffic recorded data along the morning rush hours (7:30–9:30). Moreover, it represents an example of how data was extracted. For instance, 1–4 represent the total number of each vehicle type that is leaving leg one into leg number four. Furthermore, the total column at the table represents the total number of vehicles that are leaving from each leg at the roundabout to other legs. Air quality was also monitored during the same period, in a single site at each intersection that is located downwind [14], using Genesis portable air monitoring made by Thermo Fisher at around 15–30 m from the intersection. The measurement was taken every fifteen minutes then the hourly average was used to represent the concentration at peak hour. Finally, modelling and data analysis were performed using MATLAB (7.14).

In order to minimize the data input and simplify the model structure, input selection was implemented. Initially, five inputs were used against each output; these were NO_x and CO₂, respectively. The inputs represent vehicle average speed, traffic delay per second, percentage of mini trucks (%MT) (2.5 PCU), heavy truck percentage (%HT), and the total of heavy and mini trucks (%H&M). The optimum pair combination (input-output pair) was then determined by searching for the combination with lowest Root Mean Square Error (RMSE). The selection of optimum input number was based on a single iteration using the general bell shape fuzzy function and two membership functions by using a hybrid of least-squares and back-propagation gradient descent methods. In addition, the model performance was evaluated using the following statistical equation [15, 16].

Where X_t is the actual output and X_o is the predicted output, n is the number of the outputs.

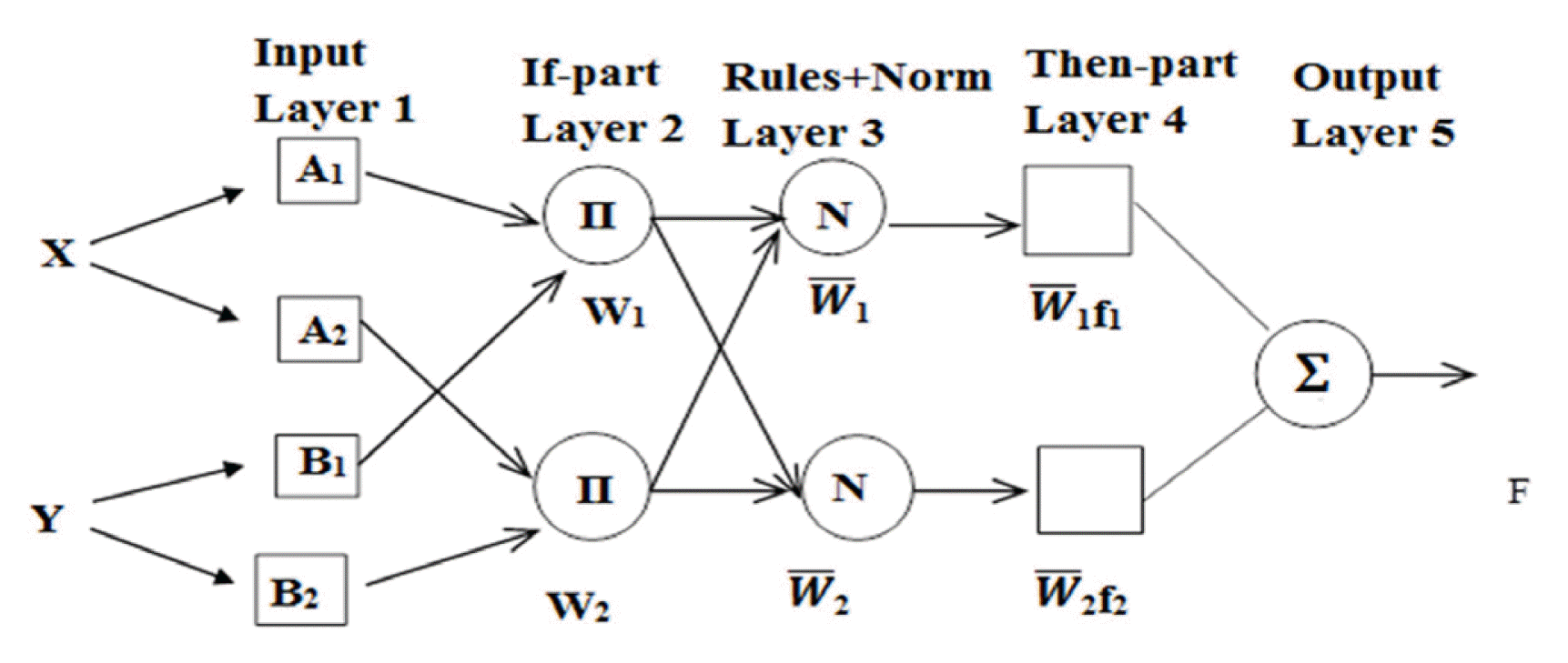
ANFIS is a multilayer feed-forward network; it performs a fuzzy logic function on incoming signals. To build the fuzzy logic structure, it is essential to (i) select the model inputs (ii) determine the membership functions, and (iii) generate the fuzzy rules. Meanwhile, minimizing the model error needs an optimizing epoch’s number, membership type and number. During the training phase, the shape of the membership function was modified in order to define the relation between input and output. This stage was repeated on several occasions (epochs) until the desired convergence was acquired (usually until the specified minimum square error between the ANFIS output and the actual one is achieved). However, for a first-order Sugeno fuzzy model, a common set of two fuzzy rules and a set of if-then rules are described as follows:

where A_i or B_j is a linguistic label (grade), such as “low” or “less”, and p₁, q₁, p₂, q₂ are the design parameters that are determined by the system developer [17]. Fig. 2 presents the ANFIS model structures, where the circular nodes are fixed and the square nodes have parameters to be learned. The shown five layers are characterized by training and testing phases. The model developer has the capability to choose among the available membership function types in accordance with system demand, simplicity, speed and convenience. The membership function is a parameterized function in which any changes in the corresponding parameters produce a change in the function shape. However, the selection of membership function should fall between 0 and 1 [18].

In this study, to develop MANFIS structure, several steps were implemented. First, optimizing the number of inputs and then determining the best input-output combinations by searching for the lowest error RMSE for training and checking. After that, altering the type of membership functions to determine the best one. Finally, determining the number of membership functions that reduce the RMSE [19, 20].

The collected input variables were divided into training (the odd readings) and testing (the evenreadings). The available variables that may affect vehicles (gasoline and diesel) emissions were selected. It was imperative to choose the factors (inputs) that are relevant to the simulated system. The summary of the optimum twelve inputs and their combinations are shown in Fig. 3. To obtain these results, twenty-five combinations were tested. These combinations were single input-output, double input-output and tribal inputs-output. For levels of single input, the total heavy and mini trucks, and car speed, represent the best results with training RMSE are equal to 494 and 731 and checking RMSE are equal to 1,357 and 1,214, respectively.

For double inputs, the best combination is between the percentage of heavy trucks and average vehicle speed, its training RMSE equalled 0.005 and checking RMSE equalled 1,300. However other double inputs combination has relatively similar results, which combination is between the percentage of heavy trucks and the percentage of mini trucks which has RMSEfor training equals to 303 and RMSE for checking equals to 861. For three inputs and single output, the best combination is between the average car’s speed, percentage of heavy trucks and percentage of mini trucks as RMSE_training = 0.002 and RMSE_checking = 973. However, using three variables as inputs for the model did not significantly enhance performance. Thus, the optimum number of inputs is assumed to be two, and the best combination is between the heavy truck percentage and vehicle speed.

Fig. 4 shows a summary of the best input combinations for modelling NO_x by testing all twenty-five possible combinations for single, double and tribal inputs. For a single input and one output that is NO_x, the percentage of heavy truck represents the best input with RMSE_training = 59.2 and RMSE_checking = 489.4, respectively. While for the combination of two inputs, the optimum one is between the delay and percentage of heavy trucks, its results are RMSE_training = 59.02 and RMSE_checking = 167.6, respectively. However, for NO_x modelling the combination of two input variables is considered as the optimum combination, since increasing the input number does not enhance the process significantly as shown in Fig. 4.

The performance of two input-output combinations for CO₂ and NO_x modelling is shown in Table 2. For carbon dioxide, the best representing pair combination is number five that is between the vehicle speed and the percentage of heavy trucks with RMSE_training equals 0.06 and RMSE_testing equals 1,300.7. However, the high testing error may be due to limited training readings which could have been avoided by increasing the number of readings. In addition, the first combination generates a smaller error for the training phase, but it is not considered due to its high testing phase error. On the other hand, for NO_x modelling, the traffic delay and the percentage of heavy trucks are considered as the optimum input pair. It produces 0.02 and 253.0 for RMSE_training and RMSE_testing, respectively.

After selecting the best input combination for both CO₂ and NO_x the best membership functions were determined. This was done by choosing from eight types of membership functions as shown in Table 3. In this phase, the hybrid training algorithm has been used. Furthermore, three membership functions and three epochs were implemented during the search process. The results show that the triangular membership function best represents CO₂ emission with RMSE_training = 0.05 and RMSE_testing = 1,034.2. While for NO_x modelling the best membership function is two-sided Gaussian with 0.007 and 241.7 for RMSE_training and RMSE_testing, respectively.

To accomplish the MANFIS structure, the optimum number of membership function was determined by keeping the epoch number constant (3 epochs) and altering the number of membership functions from 2 to 7. However, the selected optimum input combinations for both CO₂ and NO_x were used in this search. The optimum number of membership function was selected based on the generated smallest RMSE for training and testing phases. Table 4 shows the performance of the model with different function numbers. The best performance for both CO₂ and NO_x was achieved with three functions. The training RMSE of CO₂ and NO_x were 0.05 and 0.007, respectively, while for the testing phase it was 1,034.2 and 241.7 for CO₂ and NO_x, respectively. However, as shown in Table 4 increasing the numbers of membership functions does not enhance the model performance.

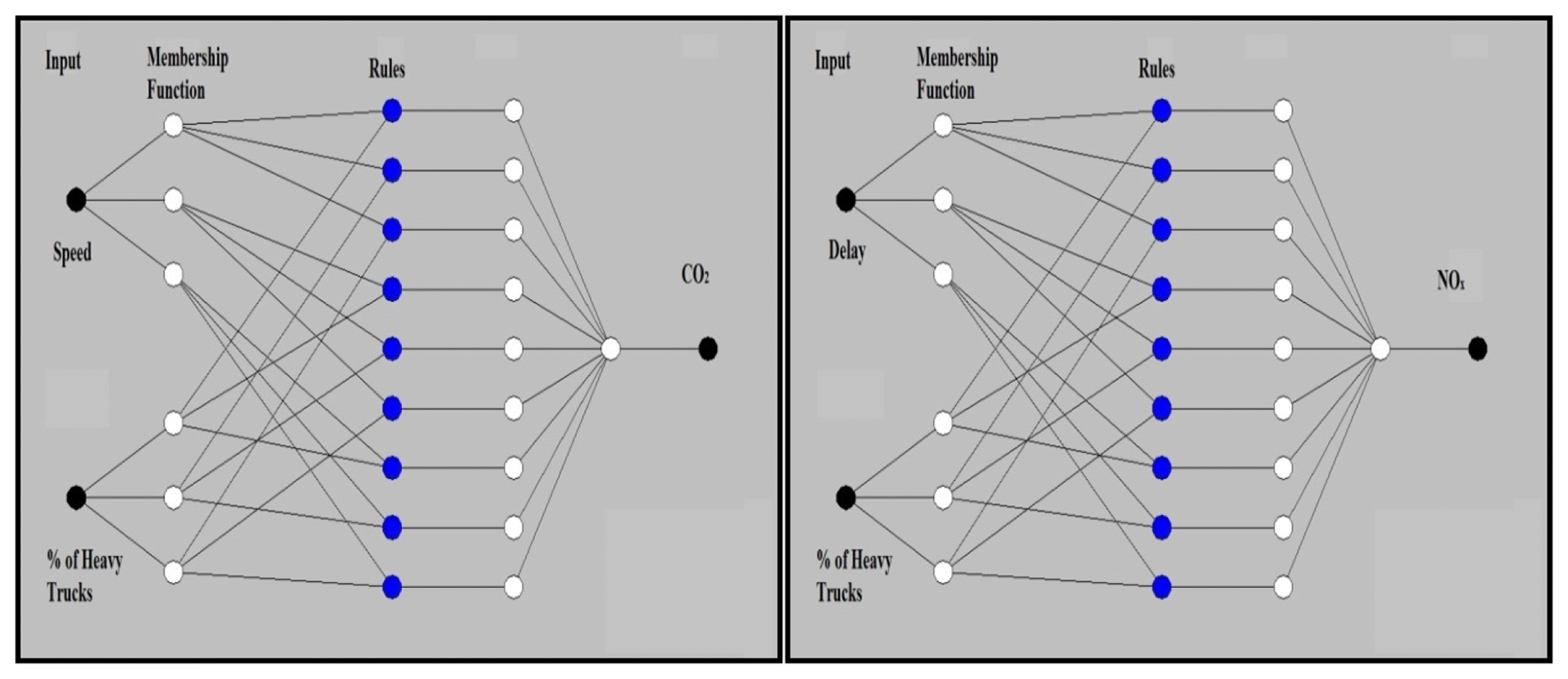
Developing the model structure by applying MANFIS enhances the overall modelling performance. For instance, it reduces the training RMSE for CO₂ by 16% and for NO_x by 65%, respectively, while it reduces the testing RMSE for CO₂ by 71% and for NO_x by 4%, respectively. Finally, the final MANFIS structure shown in Fig. 5 illustrates structures of MANFIS model for both CO₂ and NO_x, respectively. It shows the two inputs, membership functions, the three membership functions, the nine fuzzy rules and the desired output.

Fig. 6 shows the effect of the vehicles’ speed and percentage of heavy truck on CO₂ emission. For instance, for a speed value of 10 km/h, as the percentage of heavy trucks decreases, CO₂ emission increases. This is related to the increase the number of lighter, or gasoline trucks which have more CO₂ emission than the heavy truck [6]. On the other hand, increasing the speed will reduce CO₂ emissions. This goes back to different densities of diesel and gasoline. Thus, the consumption varies, and diesel consumption is less than gasoline.

Fig. 7 shows the effects of delay and the heavy truck percentage on NO_x emission. The NO_x emission can be divided into two categories. The first being 20 s per vehicle; in this region, increasing the percentage of trucks will decreased the NO_x emissions. Otherwise, the second region is for delays of more than 20 s; in this region, increasing the percentage of heavy truck increased the NO_x emission. Moreover, the highest NO_x emission was at the largest delay (55 s) and highest heavy truck percentage. Increasing the heavy truck percentage reduced the traffic movement and increased the waiting time for all vehicles at the road; therefore, emissions increased. In addition, heavy trucks, usually diesel vehicles, comparatively emit higher NO_x than gasoline vehicles during times of being stationary. Therefore, its contribution is tangible for NO_x emission [21].