1. Introduction
Due to limited water resources in the coming era, the role of water reuse, especially treated wastewater in agriculture is highly promising. The status of irrigated and rain-fed agriculture in the world is directly alarming us to the need for better irrigation scheduling to select optimum decision [1–3]. As far the material recovery and reuse strategies are concerned, the industrial effluents provide a better choice, in addition to the required environmental compliance. Cadmium, zinc, copper, nickel, lead, mercury, chromium are some of the metals often detected in industrial wastewater originating from mining, paint manufacturing, printing, smelting, pesticides, tanneries, petroleum, battery manufacturing, etc. [4, 5]. However, it is also important to note that toxic compounds like hexavalent chromium possess carcinogenic properties and can lead to corrosive effects in the intestinal tract of living beings [6, 7]. Because of their hazardous nature, they have to be removed before being discharged into the lakes, streams or any other water bodies.
Since the traditional methods for heavy metals removal such as chemical precipitation, solvent extraction, ion-exchange, reverse osmosis, etc. being very costly, industrialists and researchers are always interested in low-cost, eco-friendly and sustainable alternatives [8–10]. Considering the water resources constraints, reuse of treated wastewater for irrigation is demanding the continuous efforts to maintain good chemical quality in rivers and groundwater. In this regard, it is interesting to explore the viability of crop residues for the treatment of wastewater, which can, in turn, be used to irrigate the same crops. Among the physico-chemical treatment processes available, adsorption has been found to be effective in removing metals from aqueous solutions. Research on sustainable technology for the removal of Cr (VI) from wastewater has resulted in extensive evaluation of adsorption properties of natural materials such as modified wool [11, 12], orange peel [13], different types of sawdust [14–21], exhausted coffee and tea [22], different types of moss [23, 24], peanut hull carbon [25, 26], palm [27], rice husk [28], durian shell waste [29], landfill clay [30], guar gum [31], Spirulina sp. [32], quaternary ammonium salt [33] and cork waste [34].
In this study, the efficacy of cassava peel and rubber bark powder for the removal of Cr (VI) metal ions has been analyzed which are largely grown in southern India as plantation crops. Considering the irrigation water requirement, these crops are highly tolerant to salinity, heavy metals and other water quality issues [35–37]. Cassava waste consists of ligands such as hydroxyl, sulphur, cyano and amino groups which could bind heavy metal ions. Considering the usage of cassava peel as an adsorbent, recently a few studies have been reported about the biosorptive capacity of cassava peel [38–43]. However, related to the adsorption studies using rubber tree bark, we could not find any literature except the study of chemically activated rubber wood sawdust for the removal of copper from industrial wastewater [44–46].
While exploring novel adsorbents for developing an ideal adsorption system, it is essential to establish the most appropriate adsorption equilibrium correlation [47, 48], which is indispensable for reliable prediction of adsorption parameters. In this perspective, an understanding of the adsorption isotherm models can give insights into the pollutant-adsorbent interactions for optimizing the mass transfer mechanism. Linear regression method is the most widely approach to determine the most fitted isotherm model, which helps in evaluating the model parameters based on their goodness fit to the experimental data. However, use of kinetic adsorption models has become crucial for better understanding the mass transfer phenomena at the solid-liquid interphase which can simplify the estimation of rate-limiting step [49–51].
The study of chemical kinetics even in homogeneous systems is quite complex and arduous. The investigation of rates of chemical reaction and molecular processes are important to determine the extent of equilibrium mass transfer as well as to explore the possibilities of mass transfer limitations [52, 53]. Since these kinetic models often describe the reaction at the solid-solution interface, varying surface phenomena has led to the development of multiple site models. However, as natural sorbents frequently exhibit functionally non-uniform surfaces, heterogeneous reactive site rate models have been suggested over simplified rate expressions [54–56]. In several experiments conducting adsorption of heavy metals onto adsorbents, multi-site adsorption models were proposed to represent the temporal dependency of mass transfer kinetics [49]. It is based on the classification of the sorption sites into instantaneous and time-dependent fractions representing the effect of heterogeneity on mass transfer. The pseudo-second order kinetic equation has always been associated with the model of two-site-occupancy adsorption.
In this study, we demonstrate the applicability of different multiple-site models to explain temporal variation in the removal efficiency of the heavy metals with different bio-sorbents. The focus of this paper is to understand the kinetics of mass removal of Cr (VI) from aqueous solution using cassava peel and rubber tree bark. As far as the literature survey is concerned, cassava peel has been introduced for the adsorption studies only very recently [38–43] but the usage of the same for the removal of Cr (VI) metal ions from the aqueous solution is yet to be understood. It is also observed from literature that the usage of rubber bark tree for the removal of heavy metals from wastewater is very limited. A comparison of the results with the classical isotherm models is also intended to reveal the importance of addressing the heterogeneity in mass transfer due to surface properties.
2. Materials and Methods
In order to evaluate the performance of the selected adsorbents in the aqueous solution of heavy metals, it is necessary to establish the optimum conditions of various process parameters through batch experiments. Realistic estimation of these variables is crucial in explaining the mass transfer rate and mechanism during biosorption.
2.1. Adsorbent Preparation
The adsorbent materials (cassava peel and rubber tree bark) were collected in their raw form in small strips (4–5 cm length) from the field and were subjected to a series of washing, dehydration and dehumidification in order to overcome the problems during wet grinding to make into powder form. Due to the surface modification resulted from temperature alterations, they were ground properly in this way and the materials are segregated over a series of 600, 425, 300 and 150 micron Indian Standard sieves. Based on the physical analysis, cassava peel possesses comparatively larger apparent density (7.8%) and surface area (24.2%) than rubber tree bark although they were ground to the same average particle size (Table 1). Similarly, stock solution of adsorbate (Cr (VI)) was prepared by taking 141.4 mg of potassium dichromate (Merck India) and dissolved up to 1000 ml mark of the volumetric flask to give a stock solution of concentration 50 mg/L. This stock solution was diluted to the desired concentration for different experiments.
2.2. Initial Batch Experiments
The critical environmental parameters which influence the adsorption phenomenon, viz. pH, adsorbent dose, time of contact and effect of concentration of Cr (VI) ions were investigated by conducting a series of batch experiments by varying one parameter at a time. These experiments were conducted using temperature-controlled orbital shaker (Trishul Equipment, Mumbai) at 170 rpm at a temperature of 30 ± 10°C by adding varying quantity of adsorbents into 25 mL of synthetic metal sample taken in 250 ml conical flask. The samples were filtered through Whatman A40 filter paper and the filtrates were analyzed for residual Cr (VI) by using Spectrophotometer (Genesys 20, Thermo Spectronic, India) at 540 nm wavelength after complexing with diphenylcarbazide.
The pH was optimized after studying for a range between 2 and 11 (Orion 420A+ pH meter, Thermo Electron Corporation, India) for maximum dissolved mass removal from the aqueous solution having an initial concentration of Cr (VI) as 50 mg/L, dose of cassava peel as 3.5 g/L and dose of rubber tree bark as 8 g/L. In the next step, the effect of adsorbent dose at the selected pH was investigated by varying biomass concentration in the range of 1 to 20 g/L for each adsorbent in a similar way. The effect of contact time was determined by drawing aqueous samples after 5, 10, 15, 20, 30, 45, 60, 90, 120, 150, 180, and 240 min which are filtered and analyzed for the residual metal concentration. Further, the impact of initial metal ion concentration on the adsorption efficiency was investigated by varying the initial Cr (VI) concentration from 60 to 350 mg/L for keeping the other conditions at optimum.
2.3. Batch Isotherm Experiments
Batch isotherm experiments were carried out in 250 m conical flask kept at 30°C in a horizontal shaker by varying the initial metal concentrations from 60 to 350 mg/L under optimal contact time (240 min) and optimum adsorbent dose (3.5 g/L of cassava peel and 8.0 g/L of rubber tree bark). By measuring the concentrations at the initial time and at equilibrium, maximum adsorption capacity as well as removal efficiency were calculated. Further experiments were conducted by changing the pH of the solution before addition of biomass by using 1N HCl, 0.1N HCl, 1N NaOH and 0.1N NaOH in order to check the suitability of various isotherm models under study for adsorption of Cr (VI) ions by both the adsorbents.
2.4. Batch Kinetic Experiments
Batch kinetic experiments were performed at an initial Cr (VI) concentration of 50 mg/L by varying contact time viz. 2, 5, 10, 15, 30, 45, 60, 90, 120, 180, 240 and 300 minutes. Samples were withdrawn at different time intervals and were analyzed for residual metal ions concentration. Further experiments were conducted for different initial Cr (VI) metal concentrations viz. 11.5, 27.63, 49.23 and 97.8 mg/L under optimum adsorbent dosage. The effect of variation of adsorbent dosage for different initial metal concentration on the kinetics of adsorption was also analyzed in this study. By conducting triplicate experiments, the percentage mean error during experiments was found to be about ± 10% from the average value.
3. Results and Discussion
3.1. Evaluation of Optimum Conditions for Maximum Mass Removal
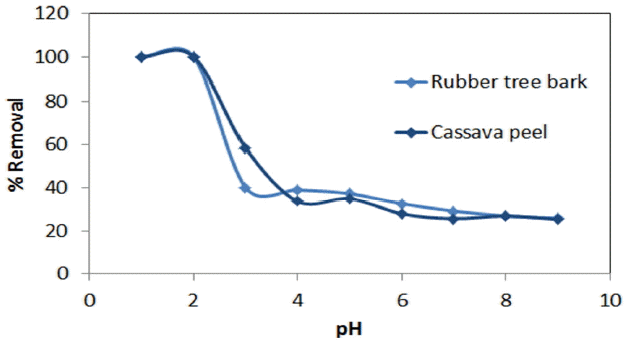
Earlier studies indicated solution pH as an important parameter affecting biosorption of heavy metals [51, 54]. It was observed that maximum removal efficiency of Cr (VI) was found to be 99.88% for rubber bark and 98.12% for cassava peel at pH of 2 (Fig. 1). This behavior can be primarily attributed to the presence of surface-charged functional groups of the biomass which in turn influenced by the pH of the solution. Higher Cr (VI) adsorption at lower pH (~2) could be explained in terms of the electrostatic attraction between the negatively charged chromium species and positively charged functional groups on the surface of biomass cell wall. But at higher pH values, the number of functional groups carrying a net negative charge is more, which tend to repel the anions [54]. However, the reduction in removal (30%) is observed at pH values beyond 2, which is concerned with instantaneous overcharging of surfaces and subsequent charge reversals [54–56]. The results also signify the need for acidification as a suitable pre-treatment for enhancing the mass removal at higher pH range.
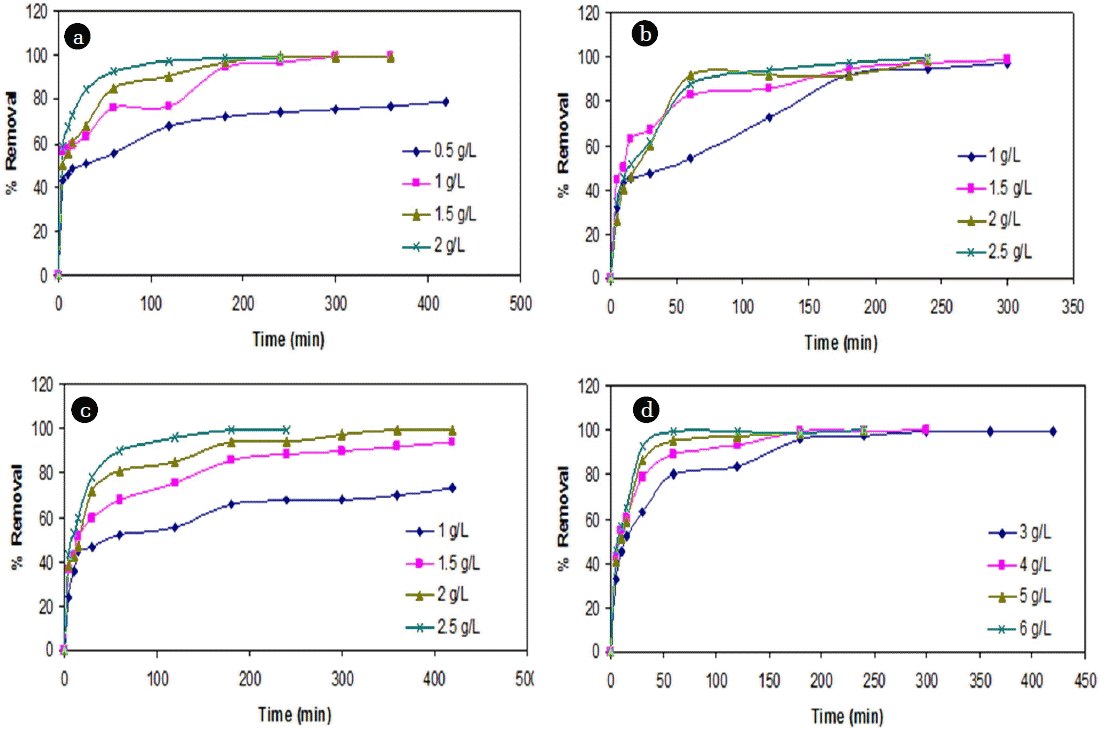
The maximum biosorption of Cr (VI) ions was attained at adsorbent dose of 3.5 g/L and 8 g/L of the biomass for cassava peel and rubber tree bark respectively. The synchronous increase in removal efficiency is quite obvious because of the increase in adsorption site at a higher adsorbent dosage. Further, when the dosage is increased beyond optimum dose, there is little or no further adsorption of metal ions as a consequence of partial aggregation of biomass, resulting in decrease in effective surface area available for biosorption. However, it is important to maintain maximum removal at optimum dosage, thereby minimizing the costs involved and making it a favorable and cheap alternative.
It was observed that the removal efficiency of Cr (VI) ions onto both the adsorbents increased with increase in contact time and attained a maximum removal at 240 min (Fig. 2). Beyond optimum contact time, there was significant reduction in removal efficiency due to the possible desorption [51]. The effect of initial metal ion concentration was investigated by varying the initial concentration in the range of 60 to 350 mg/L for Cr (VI). It was observed that at lower concentrations, adsorption efficiency varied significantly and the optimum dose was found slightly higher than the expected doses. The results are in agreement with the similar studies in literature [22, 26].
3.2. Evaluation of Equilibrium Models
Evaluation of inter-phase mass transfer rate can be simplified by the assumption of local equilibrium (LEA) which represents idealized sorption with instantaneous mass transfer [57]. The differential uptake of heavy metals onto the surface of the biosorbent can be effectively characterized by separately evaluating the kinetic and equilibrium mass transfer. As seen from the physiographic properties of the selected biosorbents, it is hard to assume which isotherm they would follow since the activity of the sorption sites can invariably change during the mass transfer. Hence, a comparison was performed here with five equilibrium models such as Langmuir, Freundlich, Temkin, Dubinin-Radeshkevich and generalized isotherm to assess the most suitable equilibrium model for Cr (VI) adsorption onto cassava peel and rubber tree bark.
3.2.1. Langmuir isotherm model
Langmuir equation is based on the assumption of a structurally homogeneous adsorbent where all sorption sites are identical and energetically equivalent [58] which can be expresses as:
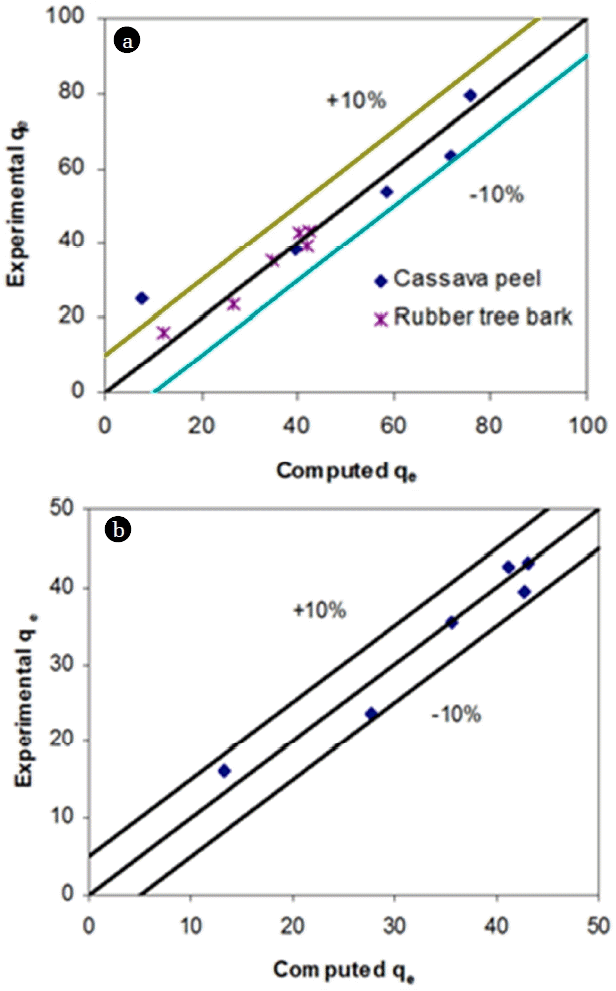
Where qe is solid phase sorbate concentration at equilibrium (mg/g), Ce is aqueous phase sorbate concentration at equilibrium (mg/L), Qm is Langmuir isotherm constant (mg/g), and b is Langmuir isotherm constant (L/mg). In adapting the Langmuir isotherm to solution chemistry, the idea of an upper limit to surface adsorption has been verified. The linearity of isotherm and high coefficient of determination (R2) values (0.986 for cassava peel and 0.997 for rubber tree bark) indicate that adsorption follows Langmuir model over the selected concentration ranges (Table 2). However, it was observed that the isotherm models were best fitted at pH 2 for Cr (VI) for both the adsorbents. The separation factor (RL= 1/(1+b Co)) was found to be varying between 0.21 and 0.58 for cassava peel, and between 0.22 and 0.62 for rubber tree bark, indicating the suitability of Langmuir isotherm for the range of initial Cr (VI) concentrations. This was further confirmed by the close fit between experimental and model values of Qm (Fig. 3).
3.2.2. Freundlich isotherm model
Freundlich isotherm model describes reversible adsorption and is not restricted to the formation of a monolayer unlike Langmuir isotherm model. The empirical equation can be expressed as:
Where KF is Freundlich constant (mg/g) and 1/n is the heterogeneity factor. Based on the experimental results, cassava peel showed a better adsorption (R2 = 0.989) compared to rubber tree bark (R2 = 0.907) (Table 2). This can be inferred from the difference in the physiographic properties of the adsorbents such as particle density and surface area (Table 1) and is confirmed by previous studies [59, 60].
3.2.3. Redlich-Peterson (R-P) isotherm model
A hybrid mechanism of adsorption was proposed by Redlich-Peterson (R-P) isotherm model by incorporating both the Langmuir and Freundlich equations, which can be expressed as:
Where KR is R-P isotherm constant (L/g), αR is R-P isotherm constant (l/mg) and β is the exponent which lies between 1 and 0. A general trial-and-error procedure was used to determine the best coefficient of determination (R2) as well as the three isotherm constants (KR, αR and β) from the linear plot of ln(Ce) against ln[KR(Ce/qe) – 1] by varying the value of KR, to yield maximum optimized value of R2 (Table 2, Fig. 3). Based on the linear regression analysis, R-P isotherm was most suitable for both cassava peel and rubber tree bark, followed by Langmuir and Freundlich isotherm. We hypothesis that, this can be either due to homogeneous adsorption independent of temporal variation in surface properties or existence of multi-sites for enhancing the mass transfer.
3.2.4. Temkin isotherm model
Temkin isotherm assumes that the fall in the heat of sorption to be linear rather than logarithmic, as implied in the Freundlich equation [51]. It can be expressed as:
Where T is the absolute temperature in Kelvin and R is the universal gas constant (8.314 J mol−1K−1). The constant bT is related to the heat of adsorption and AT is the equilibrium binding constant (Lmol−1) corresponding to the maximum binding energy. The applicability of the Temkin isotherm was analyzed using a linear plot between qe and ln Ce at constant temperature and the model constants (bT and AT) were evaluated (Table 2). The regression analysis indicated a lesser linear fit compared to the previous isotherm models for both adsorbents. This gives insight to the relative influence of chemical kinetics over the thermodynamic effect where the heat exchange is minimal compared to the inter-phase mass transfer [48].
3.2.5. Dubinin-Radeshkevich (D-R) isotherm model
The D-R model has been generally used to express adsorption based on pore filling mechanism with a Gaussian energy distribution on heterogeneous surface, and is written as:
Where K (mol2 kJ−2) is a constant which relates to the adsorption energy; and the model parameter ɛ can be calculated as:
The values of Qm obtained from D-R model were found to be less compared to the Langmuir model prediction (27.2% and 19.6% for cassava peel and rubber tree bark respectively) (Table 2). It also resulted in poor linear fit for both adsorbents compared to other isotherms under consideration. This can be attributed to the specific nature of the adsorbents showing high surface uniformity where pore filling is not favored at high metal concentrations, thereby violating the assumptions of D-R model. The results also confirmed that the physical and chemical processes of biosorption cannot be distinguished easily with these model parameters.
3.2.6. Generalized isotherm model
Linear form of the generalized isotherm can be written as [51]:
Where KG is the saturation constant (mg/L); and Nb is the cooperative binding constant. The results showed that the model is fitting well for rubber tree bark (R2 = 0.985), while poorly fitting for cassava peel (R2 = 0.630) for the adsorption of Cr (VI) (Table 2). This can be due to the high Qm values for cassava peel as obtained from the Langmuir model showing the sensitivity of the model towards saturation capacity which is purely sorbent-specific.
From the values of coefficient of determination based on linear regression analysis (Table 2), it can be inferred that R-P model fitted well for adsorption of Cr (VI) ions onto both the adsorbents. However, maximum adsorption capacity obtained from this model for Cr (VI) adsorption was found to be higher for cassava peel (79.37 mg/g) followed by rubber tree bark (Qm = 43.86 mg/g) which were in close agreement to the experimental values (within 10% error margin), confirming the suitability of the Langmuir model for both cassava peel and rubber tree bark (Fig. 3). This is in close agreement with the published results on similar studies [38, 44].
3.3. Testing of Kinetic Adsorption Models
In order to investigate the mechanism of sorption such as mass transport and chemical reaction processes and to evaluate potential rate-controlling steps, six kinetic models (First Order kinetic model, Second Order kinetic model, Pseudo-First Order model, Pseudo-Second Order kinetic model, Intra-Particle Diffusion model and Elovich kinetic model) were tested in this study. The experiments were performed by varying the contact time, by keeping the adsorbent dose, initial concentration and temperature constant and the details of the linear regression fit were presented in Table 3.
3.3.1. First order (FO) kinetic model
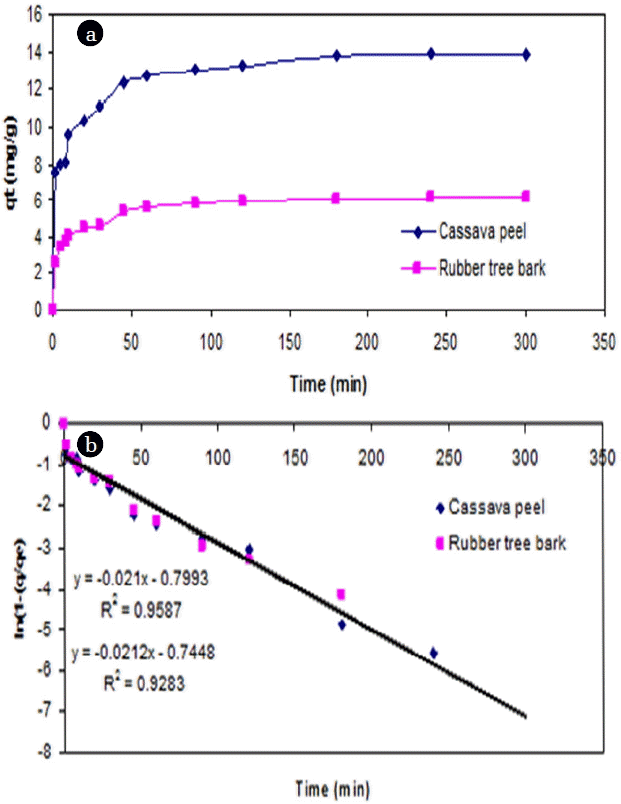
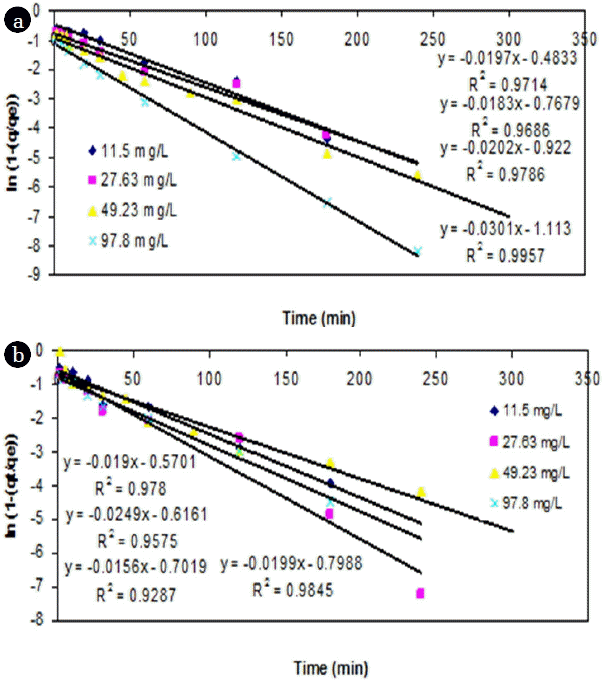
From the point of view of fitting with linear regression models, a linear plot of t versus ln(1-(q/qe)) showed a lesser degree of fit (<0.95) for both adsorbents from the experimental data (Fig. 4). However, the adsorption of Cr (VI) ions exhibited saturation kinetics after the first hour as the quantity of bound metal ions reached saturation for both the adsorbents.
The variation in the initial Cr (VI) had resulted in significant increase in slope and intercept values for cassava peel compared to the rubber tree bark (Fig. 5). It showed that when the Co of Cr (VI) increased by 140.3%, 78.2% and 98.7%, the intercept of FO model for cassava peel also increased by 59%, 19.5% and 20.7% respectively, whereas the increase with rubber tree bark was quite marginal (8.8%, 12.9% and 14.3%). This can be attributed to the limit of saturation of sorption sites at higher dosage as observed in Fig. 4. Similar results were also found in literature regarding the impact of higher dosage on adsorption efficiency [42, 61].
3.3.2. Pseudo first order (PFO) kinetic model
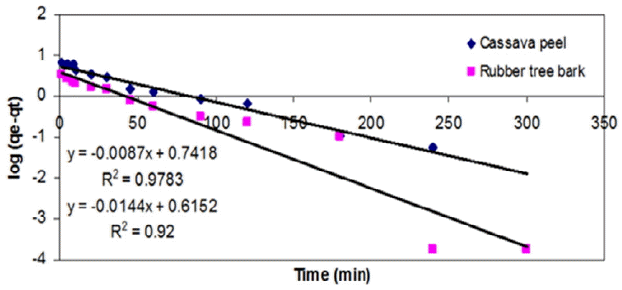
As an alternative to the previous model, the PFO model was applied to the experimental results by plotting log (qe – qt) versus t and the model fitness was compared in terms of R2 value and the prediction of rate constant, k1. It was observed that PFO model gave relatively a better fit to the experimental results on cassava peel than those for rubber tree bark (Table 3 and Fig. 6). Yet, it cannot be suggested as a representative model due to the validity over a limited period of time and large variation in equilibrium adsorption capacity (qe).
3.3.3. Second order (SO) kinetic model
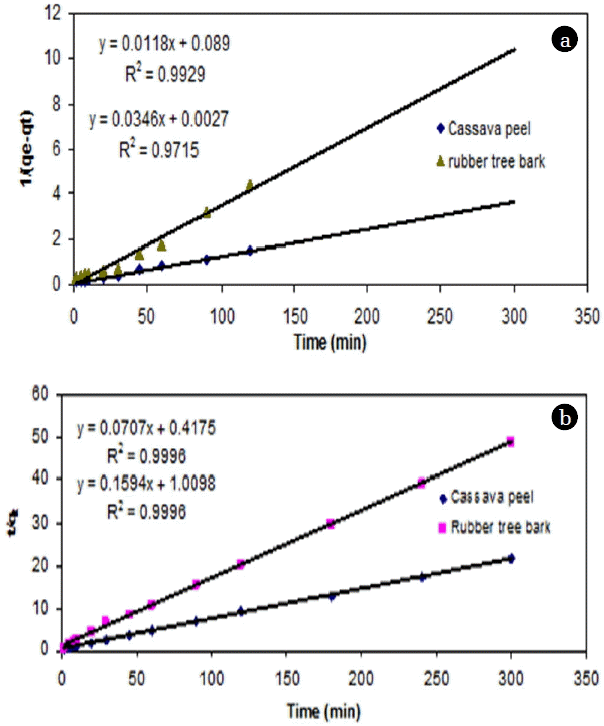
It has been commonly observed that the sorption rate is very rapid at the beginning of the process and becomes slower as equilibrium is approached. In order to understand the significance of chemisorption, the experimental results were fitted with SO kinetic model. The experimental data was found to be best fitted for removal of Cr (VI) by cassava peel (R2 = 0.99), but to a lesser extent for rubber tree bark (R2 = 0.97) (Table 3, Fig. 7(a)).
3.3.4. Pseudo second order (PSO) kinetic model
Results from the linear plot between t/qt and t indicated a very close fitting (>0.999) of experimental data for PSO kinetic model (Table 3, Fig. 7(b)). In addition, the calculated qe values also agree well with the experimental qe values. Hence, the adsorption of Cr (VI) onto cassava peel and rubber tree bark can be described well by this model, indicating chemisorption to be the rate limiting step. This is in accordance with similar studies on adsorption with heavy metals [23, 24].
3.3.5. Intra-particle diffusion (IPD) model
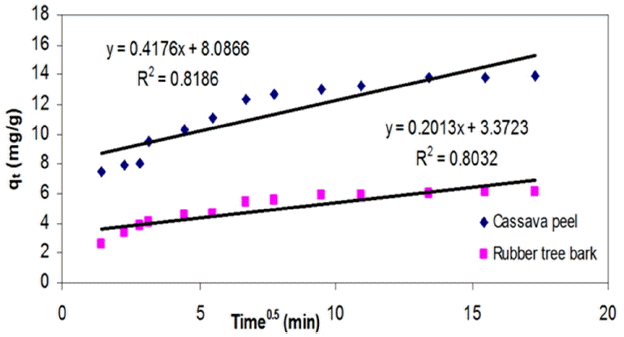
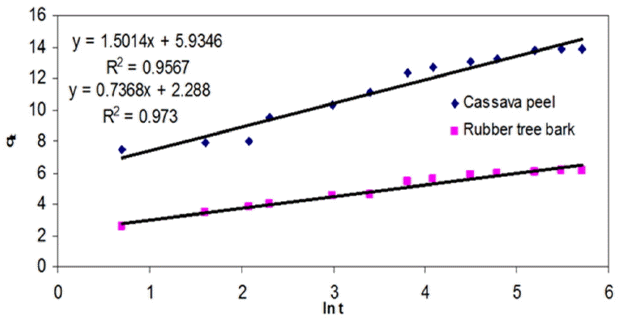
As observed so far, the chemical potential of the sorbent-metal interactions were found to have an upper hand in controlling the mass transfer compared to physical mechanisms like pore filling or intra-film diffusion. On the basis of the change in availability of metal ion concentration over a period of time, the significance of intra-particle diffusion was analyzed by estimating the model constants ki from the slope of the plots of qt versus t1/2. The values of intercept represent the boundary layer thickness, which in effect account for the increase in adsorption capacity. Even though regression analysis resulted in lowest fit (< 0.85), the intercept was observed to be increasing with increasing initial metal concentration (Table 3) which can be interpreted as the rate-limiting step for the adsorption of Cr (VI) unto both the adsorbents.
As seen from Fig. 8, the trend of the experimental data revealed existence of multi-linearity where two or more steps may be involved in adsorption [62, 63]. The initial portion represents instantaneous adsorption stage, followed by a gradual adsorption stage where intra-particle diffusion seems to be rate-controlling. The third portion is the final equilibrium stage where intra-particle diffusion starts to slow down due to the low adsorbate concentrations in the solution. This indicates that transport of metal ions from the solution (through the sorbent-liquid interface) to the available surface of sorbent as well as to the micro-pores may be responsible for the high uptake of metal ions. Similar findings were also reported by Namasivayam and Ranganathan [9] for the uptake of Cadmium on a waste product from fertilizer industry. The deviation of the curves from the origin also indicated that intra-particle transport is not the only rate-limiting step in adsorption of Cr (VI) ions onto selected adsorbents in this study.
3.3.6. Elovich kinetic model
The kinetics of chemisorption has been adequately represented in the literature by the second-order equation and the Elovich Equation [64]. It was observed that Elovich kinetic model can adequately represent the adsorption of Cr (VI) onto both the adsorbents based on the regression analysis (Table 3, Fig. 9). On the basis of the excellent fitting of both the PSO and Elovich model, it can be proposed that the predominant sorption mechanism may be chemisorption.
3.4. Comparison with Two-Site Sorption Model
The two-site sorption conceptual model is based on assumption that a fraction (f) of the mass exchange sites of the sorbents favours instantaneous sorption (S1 = fKC) and another fraction (1 – f) is considered to be time-dependent (S2 = (1 – f)KC). Two different approaches were considered in this study depending on the mode of contact of the sorption sites with the liquid concentration namely, two-site sorption model with a serial interface (TSSI) and two-site sorption model with a parallel interface (TSPI) [24]. By considering the reversible sorption kinetics between the two types of sites, TSSI model can be expressed as:
Where K1 and K2 are the forward and backward sorption rate coefficients and S1 and S2 are the associated sorbed mass respectively. Similarly, TSPI model can be used to estimate equilibrium and non-equilibrium sorption parameters as given by:
Where α and K are the sorption rate constant (h−1) and distribution coefficient (L/kg−1), respectively. By applying these kinetic models to the batch system with the assumption that time-dependent fraction obey FO kinetic model, Lee et al. [24] developed analytical solutions for TSSI and TSPI models. We have further modified them to express in the linear form as:
Where C*=Ce/C0; retardation factor, R=1+ Π MK/V; is the mass of sorbent (g); Kr is the sorption rate constant for TSSI model (h−1); V is the volume of the solution (mL); α is the sorption rate constant (h−1) for TSPI model and β is a model parameter corresponding to equilibrium fraction.
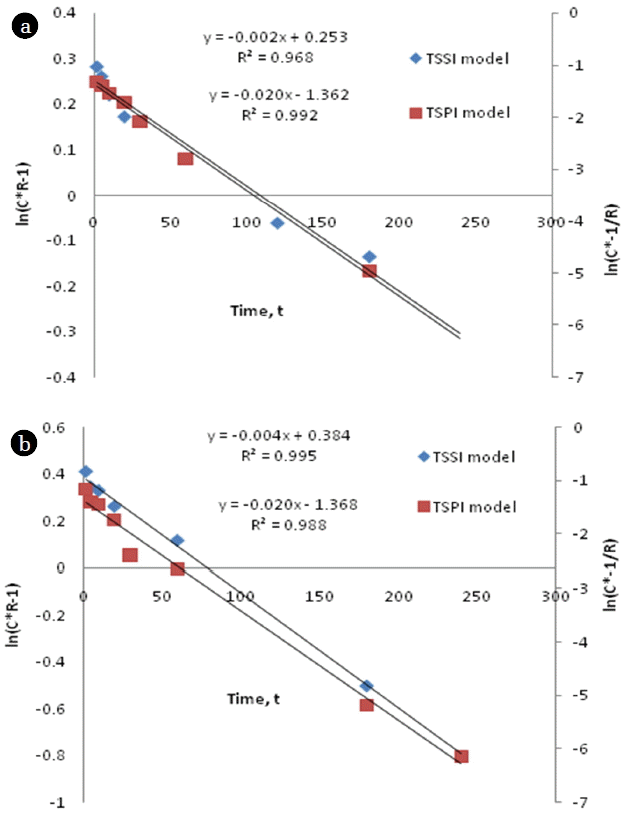
The possibility of two-site sorption models was evaluated based on the linear regression analysis of Eq. (10) and Eq. (11) for both adsorbents. It was observed that both sorbents exhibited very good fit for both two-site models even though TSPI model fitted more accurately for sorption unto cassava peel whereas TSSI model was more suitable for representing sorption unto rubber tree bark (Fig. 10). Considering the specific kinetic nature of sorption in terms of model parameters, TSPI model was found to be invariant for both the sorbents with high mass transfer rate (0.89 h−1), whereas TSSI model resulted in low mass transfer rate (5% for cassava peel and 10% for rubber tree bark) compared to TSPI model (Table 4). However, based on the surface properties of the adsorbents (size and shape of the particles), it is suggested that TSPI model can hold well under different conditions.
By comparing the model results with separate equilibrium and kinetic modeling attempts, it can be inferred the sequential process of mass transfer can be more effectively described by two-site model. During the initial stage, the exterior surface reached the saturation level due to the direct attachment to the surface; then the metal ions begin to attach to the adsorbent via the pores within the particles and were adsorbed onto the interior surfaces of the particles. Until this stage, isotherm model holds well, while the latter part of kinetic sorption can act as the rate-limiting step as explained by the chemi-sorption. With the decrease in metal ion concentration in the solution, the diffusion rate became constantly lower, and consequently, the adsorption process end up in equilibrium conditions.
4. Conclusions
Present study discusses about the kinetics of Cr (VI) removal from the aqueous solution by using two naturally available agro-waste materials (cassava peel and rubber tree bark). Apart from the estimation of removal efficiency based on batch (equilibrium and kinetic) adsorption experiments this study focuses on the suitability of various modeling approaches to evaluate the kinetics of mass transfer. A comparison of six isotherm models and six kinetic models were presented based on the linear regression fitting. The study also highlights the possibility of employing multi-site sorption model for simultaneous representation of different stages of kinetic sorption as well as identifying the rate-limiting process. The salient results of the present study are briefed here.
With the increase in the cassava peel adsorbent dose from 0.25 to 3.5 g/L the percentage removal of Cr (VI) ion increased from 26.33 to 99.95%. The percentage of adsorption increased for rubber tree bark from 1.83 to 100% as the dose increased from 0.25 to 8 g/L due to the availability of more unsaturated adsorption sites. When the dosage is increased beyond optimum dose, there is little or no further adsorption of metal ions as a consequence of partial aggregation of biomass resulting in decrease in effective surface area available for the biosorption.
Based on the comparison of isotherm models, Redlich-Peterson model and Langmuir model fitted well (R2 > 0.99) for both sorbents indicating that an upper limit existed for the adsorption over the external surface. The maximum adsorption capacity for cassava peel and rubber tree bark were found to be 79.37 mg/g and 43.86 mg/g respectively. Comparison with the Temkin isotherm model showed that the influence of chemical kinetics dominated the thermodynamic effect where the thermodynamic effect is minimal compared to the inter-phase mass transfer.
While comparing the kinetic sorption models, pseudo-second order model showed a very good fit as well as closeness to the experimental values of sorption capacity, indicating chemisorption to be the rate limiting step. This was further confirmed by the fitness to Elovich model. Unlike similar studies reporting intra-particle diffusion as the rate-limiting step, the diffusion model resulted in multi-linearity indicating the possibility of two or more steps in adsorption.
Two different multi-sites models namely, two-site series interfaces (TSSI) and two-site parallel interface (TSPI) were considered in this study depending on the type of interaction of sorption sites with the liquid concentration. It was observed that both sorbents exhibited very high fit for both two-site models. Considering the specific kinetic nature of sorption in terms of model parameters, TSPI model was found to be invariant for both the sorbents with high mass transfer rate (0.89 h−1), whereas TSSI model resulted in low mass transfer rate (lower by 5% for cassava peel and 10% for rubber tree bark) compared to TSPI model.
By comparing the model results with the conventional explicit equilibrium and kinetic modeling attempts, it can be inferred that the sequential process of mass transfer can be more effectively described by two-site model. It is also inferred that the adsorbents selected in this study (cassava peel and rubber tree bark) are efficient for the removal of Cr (VI) as a suitable alternative to other costly adsorbents.