AbstractEstimating the liquid level in an anaerobic digester can be disturbed by its closedness, bubbles and scum formation, and the inhomogeneity of the digestate. In our previous study, a soft-sensor approach using seven pressure meters has been proposed as an alternative for real-time liquid level estimation. Here, machine learning techniques were used to improve the estimation accuracy and optimize the number of sensors required in this approach. Four algorithms, multiple linear regression (MLR), artificial neural network (ANN), random forest (RF), and support vector machine (SVM) with radial basis function kernel were compared for this purpose. All models outperformed the cubic model developed in the previous study, among which the ANN and RF models performed the best. Variable importance analysis suggested that the pressure readings from the top (in the headspace) were the most significant, while the other pressure meters showed varying significance levels depending on the model type. The sensor that experienced both headspace and liquid phases depending on the level variation incurred a higher error than other sensors. The results showed that the ML techniques can provide an effective tool to estimate digester liquid levels by optimizing the number of sensors and reducing the error rate.
1. IntroductionAnaerobic digestion (AD) is a promising technology that couples wastewater treatment and renewable energy production [1]. Microbial reactions are the primary player of AD, and thus, maintaining the stability of the process parameters is essential for its function. For example, organic loading rate (OLR) is one of the fundamental factors determining AD’s biogas productivity and economic viability. Another example is hydraulic retention time (HRT), closely related to the microbe-pollutant contact time. Both parameters are dependent on bioreactor volume; therefore, the water level of the digester is a vital operation parameter [2].
Recent technology developments allow continuous monitoring of many key parameters during AD operation [3, 4]. However, some parameters, such as the chemical oxygen demand of the digestate, are yet to be monitored in real-time due to instrumental limitations [5]. It is also challenging to monitor the digester water level continuously with high accuracy. Radar or ultrasonic level sensors can accurately measure water levels in an open system, but they can be easily disturbed by the generation of bubbles and scum in anaerobic digesters [6]. Due to such limitations on direct measurement, using soft sensors can be an alternative approach to maximize estimation accuracy [7]. For example, the liquid level in a black box can be estimated if both the pressure and the density of the liquid column are known. However, the liquor in the digester (i.e., digestate) contains high concentrations of suspended solids, making it challenging to keep the digestate homogeneous in the digester. Therefore, using pressure sensors with homogeneity assumption of the digestate may lead to erroneous estimation of the liquid level in AD.
Our previous study suggested a method to overcome this limitation by predicting the unequal density profiles using multiple pressure meters [8]. A pilot-scale digester (0.33m3 working volume, 1.4 m height, 1.2 m liquid level) was operated to collect data for the water level prediction model. By collecting pressure data from seven sensors (six in the liquor and one in the headspace), density profiles of the liquid columns were derived, and the top layer’s density was calculated through prediction models. As a result, a cubic model outperformed other polynomial models as well as the traditional, two-sensors approach. Although the digestate level can be predicted with high accuracy using this method, however, the requirement for seven pressure sensors may cause investment and maintenance burdens. Because only polynomial models were tested in the previous study, there is likely room for improvement if we test other modeling approaches using the same or even less number of sensors.
Machine learning (ML) is a computational method used for prediction or classification using various algorithms [9, 10]. Recently, ML approaches are gaining popularity to generate new models for precise prediction in many research areas. For example, ML can be used to study nanomaterials for energy and environmental applications [11, 12]. Studies were conducted to develop effective photocatalysts to treat toxic pollutants such as thymol blue [13, 14]. ML has been also applied in water and wastewater engineering research. Choi et al. [15] estimated the water level of Upo Wetland with long-term data with various parameters like temperature, precipitation, wind speed, and water level in the nearby area. Comparison among four models – artificial neural network (ANN), decision tree (DT), random forest (RF), and support vector machine (SVM) – were conducted, and RF was selected as the best model. Granata et al. [16] compared SVM and regression tree to estimate water quality using parameters like chemical oxygen demand, total suspended solids, biochemical oxygen demand, and total dissolved solids. The methane composition of biogas in AD was also estimated through ANN with genetic algorithm optimization [17]. Talebkeikhah et al. [18] tried to estimate the permeability of two carbonate reservoirs with SVM, DT, RF, multi-layer perceptron, and radial basis function (RBF) neural network and showed that DT and SVM were the best models for permeability prediction. Suitability tests of soils for airfield application with the fuzzy knowledge-based system were conducted and proposed as an accurate tool [19]. Pedro et al. attempted to optimize the work conditions like time and the number of workers for optimal work of floating caissons [20]. These studies suggest that ML can be a helpful tool to generate prediction models in various areas.
This study aimed to improve the liquid level prediction approach in AD equipped with multiple pressure sensors and optimize the number of sensors by attempting various ML algorithms. Linear regression, ANN, random forest (RF), and SVM with RBF kernel were compared to each other and with the cubic model from the previous study. The pros and cons of using different ML algorithms were discussed, and the significance levels of the different pressure sensors were compared. This study offers information to decide and optimize the method to estimate the water level of an anaerobic bioreactor in real-time.
2. Materials and Methods2.1. Summary of the Research ProceduresThis research aimed to predict the liquid level of an anaerobic digester equipped with multiple pressure sensors using ML (Fig. 1). The experimental system (i.e., the bioreactor and instrumentation), data collection, and the development of polynomial models in the previous study [8] are summarized in section 2.2. Four widely-applied ML methods were utilized to predict the liquid level in this study as detailed in section 2.3 (Fig. 1). Models derived from different algorithms were evaluated by comparing the error values in the forms of root mean square error (RMSE), mean absolute percentage error (APE), and maximum APE (described in section 2.4). In addition, corrected Akaike Information Criterion (AICc) values were used to optimize the number of parameters. Finally, conclusions were made on the most desirable algorithm and parameters.
2.2. System Description and Data CollectionThe anaerobic bioreactor system and the experimental data were published previously [8]. Briefly, a pilot-scale (0.33 m3 working volume; 1.4 m height; 1.2 m liquid level) bioreactor was equipped with seven pressure sensors at approximately 0.1, 0.3, 0.4, 0.6, 0.7, 0.9, and 1.25 m from the bottom (Fig. 1). The bioreactor was operated for 175 days; the liquid level was maintained stable at 1.2 m for most of the time, while a short-term level variation (0.8–1.2 m) was applied at day 99. The bioreactor was placed in a temperature-controlled room (36°C). The anaerobic bioreactor showed a stable digestion performance in terms of pH, biogas production, and volatile fatty acid accumulation (see Rhee et al. [8] for details). All the sensor-derived data (i.e., pressure, temperature, and biogas) were recorded at an interval of one min or less.
The pressure readings (P0, P1, …, Pn) were obtained from the pressure meters (h0, h1, …, hn), of which P0 and h0 refer to the top sensor in the headspace. The apparent density of the liquid layers (ρ2, …, ρn), except for the top layer (ρ1; between h1 and h2), was determined by gravimetric relationship (Eq. (1)). Once the top layer density (ρ1) is estimated, the total liquid level (hliquid) can be calculated by Eq. (2).
where ρ is the density of the liquid column, P the pressure, g the gravitational force, and h the height. In Eq. 2,P0 (headspace pressure) is subtracted from P1 as a reference value because the anaerobic bioreactor usually keeps positive pressure at the headspace. The previous study compared polynomial models (linear to quintic) between P and ρ, and concluded that the top layer (ρ1) is well depicted by a cubic model [8].
2.3. ModelingIn this study, four new approaches implementing ML were additionally tested if they can improve the accuracy of the model: multiple linear regression, RF, ANN, and support SVM with RBF kernel. The following sub-sections (2.1.1 to 2.1.4) summarize the general features of the four methods, including their potential limitations. Supervised learning was conducted which train model by offering an example answer. All data were standardized for smooth model fitting. As the model parameters, seven pressure and one temperature readings were used for direct comparison with the previous study. The ‘train’ function in the R program’s caret package was used to search for proper hyperparameters rapidly.
2.3.1. Multiple linear regression (MLR)Linear regression algorithm is to fit model with linear function between independent and dependent variables. Linear regression is the most common approach for modeling numeric data and can be adapted to almost all types of data [21]. With accurate modeling, this method can give information about contribution in form of coefficient. However, linear regression requires assuming that the independent and dependent variables have a strong linear relationship. Additionally, this method requires a large amount of dataset for accurate modeling [22]. The accuracy of the model was assessed using a gradient descent algorithm. The gradient descent optimization algorithm is one of the most popular algorithms to perform optimization about a model. RMSE was used as the cost function while optimizing this model.
2.3.2. Artificial neural network (ANN)ANN is an algorithm that mimics the structure of human neurons. ANN is widely used for non-linear function estimation, data sorting, pattern detection, optimization, clustering, and simulation [23]. Among different types of ANN, a feed-forward neural network with a single hidden layer of five nodes was used in this study.
Three elements adjust the model’s structure: activation function, network topology, and training algorithm [21]. An activation function is an element that transforms the input signal into the output signal. A network topology includes factors like the number of nodes, the direction of information travel, and the depth of the hidden layer [21]. For example, too many nodes can be led to overfitting [24]. A proper combination of these factors can improve the accuracy of the model. The model estimates values through interaction between interconnected neurons. The algorithm aims to find out proper weights used to calculate variables. Although ANN is known as one of the most accurate modeling approaches, it usually takes a longer time than other algorithms, and the model structure is challenging to recognize.
2.3.3. Random forest (RF)RF is a model that consists of multiple DTs. DT is an algorithm for classification and prediction, that is easy to be used because of its simplicity. A DT model consists of many logical decisions like a flow chart [21]. Starting from the root node, the data are split into various nodes to reach the final leaf (or terminal) nodes. The DT tries to make an optimal model by searching for the model that maximizes the purity of the terminal modes. High purity means that it can classify or predict values with high accuracy.
The advantage of using DT lies in its speed, as DT can select useful features automatically. DT can describe some datasets more accurately than linear regression [21]. However, DT may lead to overfitting with complex datasets. To overcome this problem, the RF has been developed. The emergence of ensemble trees can improve the accuracy of the model. RF calculates value by combining all decision tree’s values. With this property, RF can handle massive datasets and is resistant to outliers during training. After combining all values, a cost function (Eq. (3)) is generated to evaluate the model.
RF uses the bootstrap aggregating (or bagging) method to avoid overfitting and correlation of the different trees. Correlation among trees disrupts accurate modeling. Bagging is an algorithm that resamples data randomly from the dataset to train the data without deletion. The data not selected for training a particular tree is called ‘out of bag’. The subsequent data subset is used to evaluate the error and correlation of the model. With these steps, RF can predict a value with high accuracy and have strength when dealing with large and noisy data [24]. However, RF cannot predict a value that the model has not experienced. For this reason, RF requires extensive learning experience.
2.3.4. Support vector machine (SVM)SVM is a computational learning algorithm based on the statistical learning theory [25]. This algorithm predicts values by finding a hyperplane that divides data with a maximum margin by converting original data into high-dimensional data. SVM tries to minimize the total cost rather than finding the accurate model for the model’s stability. For this reason, SVM is strong against overfitting [21].
Kernel function can be used to modify the dataset’s dimension for accurate analysis. There are various types of kernel functions. Finding a proper kernel type is an essential step for accurate model development. As a result, in this study, the RBF kernel was selected after comparing the linear, the polynomial, and the RBF kernels. With a proper kernel function, SVM can conduct modeling on complex data with high accuracy. However, SVM is not easy to deal with a large amount of data, and its model is difficult to understand [22]. Therefore, the step to search the proper kernel is required for accurate modeling.
2.4. Model Evaluation and Variable Significance TestThe pressure data from seven pressure sensors (P0, …, P6; from top to bottom) and the temperature data (T) were considered to be used in modeling to compare directly with the result of the previous study. Out of the seven pressure readings, three combinations were specifically tested for the models: two (bottom and the headspace readings; P6 and P0), three (bottom, top, and the headspace readings; P6, P1, and P0), and seven (all seven readings). The data was preprocessed through standardization for accurate modeling. Standardization is preprocessing method which rescales data to have one as standard deviation and zero as mean. After standardization, 747 data points were derived; 521 data points (70% of data) were used to train models and 225 data points (remaining 30% of data) were used to test the models. This study conducted model evaluation by comparing RMSE, mean APE, and maximum APE.
The importance of each variable was estimated for each type of algorithm (i.e., MLR, RF, ANN, and SVM) through a specific method. For MLR, the absolute value of the t-statistic for each variable was used. The RF used an out-of-bag score for variable importance calculation. Gevrey’s weights method, which combines the absolute value of the weights, was used to estimate variable importance for ANN [26, 27]. Finally, locally estimated scatterplot smoothing (LOESS) R2 was used for SVM models for variable importance. All variable importance was estimated using ‘varImp’ function of caret package in R.
To evaluate the proper number of parameters for the models, AICc was calculated. Akaike information criterion (AIC) is a criterion that can be used to decide on where to stop to input more the independent variables [28]. However, AIC has a problem when the number of data is not enough. To solve this problem, AICc was proposed by Hurvich and Tsai [29].
where SSE is the sum of squares error, n is the observed data’s number, and p is the number of parameters. A model with a smaller AICc value was assumed to be more accurate because AICC is in proportion to the error.
3. Results and Discussion3.1. Model PerformanceThe overall performance of the four models using different datasets (i.e., two (Table 1), three (Table S1), or seven (Table 2) pressure readings) were compared. Overall, ANN and RF showed lower RMSE than MLR and SVM. The mean APE was the lowest for RF, while the maximum APE was the lowest for ANN. The higher the number of pressure readings used in the models, the lower the RMSE and APE values were derived in general.
The MLR model did not perform well compared to ANN and RF (Table 1, 2). This result suggests that the liquid level estimation of an anaerobic digester involves complex interactions that are not able to be explained best by a simple linear combination of the variables. Within the model, all RMSE, mean APE, and maximum APE decreased with the increasing number of variables (i.e., pressure readings); these results also support that more model complexity can lead to more accurate estimation.
The SVM model showed the poorest performance in terms of the mean APE (Table 1, 2). In all cases, the performance parameter of APE was among the poor half out of the four models (i.e., the first or second highest RMSE or APE). Therefore, it could be concluded that SVM was not the best approach for liquid level prediction in our configuration. Unlike the MLR model, using more pressure data did not improve this model.
The ANN approach used in this study employed a feed-forward neural network with a single hidden layer (five nodes included) and backpropagation [30, 31]. Due to the randomness of the model build-up, ten ANN models were created and the one with the least RMSE was selected. The ANN showed superior performance than other models (Table 1, 2). The RMSE and the maximum APE of ANN were the lowest among the models tested. A lower maximum APE implies that this model had a more robust resistance to outliers than other algorithms.
On the other hand, the mean APE of the ANN model was about half of those of the MLR and SVM models, but double of the RF. Like the MLR, both the RMSE and mean APE for the ANN also decreased as the number of pressure readings increased. Although the higher number of input data (i.e., pressure readings) generally increased the accuracy of this model, no clear trend was observed for maximum APE.
In the case of RF, 500 trees were grown with a bagging number of five. RF showed the lowest mean APE and the second-lowest RMSE among the models (Table 1, 2). However, the maximum APE of RF was comparable to SVM, especially when a higher number of pressure readings were used. It could be concluded that the best RF model was achieved using two pressure readings, and a higher number of variables did not increase its accuracy. This trend was similar to SVM.
Overall, the ML-based models proposed in this study outperformed the polynomial model derived in the previous study [8]. Both the RMSE and the mean APE were the highest for the cubic model, and its maximum APE was comparable to SVM and RF (Table 2). Fig. 2 shows the observed and estimated water levels using different models. The margin between a dot and a red line means the error rate. The estimations made by the cubic, MLR, and SVM models clearly showed a more inaccurate representation of the liquid level. In addition, the cubic and SVM models likely had structural underestimation of the liquid level at 1.2 m. To summarize, the ANN and RF models showed the most successful estimation of the liquid models in our configuration.
Interestingly, RF and SVM showed higher maximum error according to the increase of the number of variables (Table 1, 2), while MLR and ANN showed better performance with more variables. This is probably due to the characteristics of the models. Thus, the initial selection of a model could be based on the number of variables available.
3.2. Importance of VariablesVariable contribution analysis is essential for accurate analysis and evaluation of layers. To evaluate the use of different pressure readings, the variable contribution was analyzed (Fig. 3). Commonly, the temperature (T) shows low or no importance to the modeling results. This is reasonable because the temperature within a stable range can hardly affect the volume or density of a liquid. Among the pressure variables, the headspace reading (P0) and the bottom reading (P6) showed high variable importance in most cases. The topwater column reading (P1) was also significant in some cases, especially when using three pressure variables (Fig. 3b). One of the reasons contributed to this observation is that this pressure meter was at the headspace (in addition to P0) in some data points with lower liquid levels. This reason may lead to another accuracy problem in the reactor. The other water column readings (P2–P5) generally had low importance on the model (Fig. 3).
One exception to this trend was SVM; this model showed relatively equal contribution from the different pressure variables. It is suspected that the SVM was affected by multicollinearity. To confirm the correlation, variance inflation factors (VIF) among parameters were calculated (Table S2). The VIF values of P2–P6 were over 10,000, and only P1 and P0 showed lower VIF values (< 100). This phenomenon can be induced by a dataset that contains highly correlated variables [32] and negatively affects the results. It was suggested that the effects of multicollinearity can be removed by removing redundant data or introducing prior information [33], which can be the case of SVM models with lower pressure variables in this study. For this reason, it is not recommended to utilize SVM with RBF kernel for liquid level prediction with multiple pressure sensors.
To determine the importance of each pressure layer in the RF and ANN models, the RMSE and APE values for models without one pressure layer were compared (Table 3, 4). For both algorithms, models lacking P0 showed significantly lower performance. It implies that the pressure meter at the headspace is essential to estimate the water level. This is reasonable because the headspace pressure is linked to all pressure values within the bioreactor. Removing some layers, such as P1, lowered the errors, indicating that having more parameters does not necessarily improve the model. This is probably because P1 experienced both water (liquid) and air (headspace) phases depending on the liquid level. Therefore, avoiding a pressure sensor at an amphibious level could be suggested. Overall, the absence of a parameter with a higher contribution was not critical to the model’s performance, suggesting not as many as seven pressure parameters are required for accurate modeling.
3.3. AICc TestThe AICc values were obtained to assess further the importance of variables (Fig. 4(a), (b)). For MLR and SVM, models with three to six parameters showed similar results. For RF, models with three parameters (from top or bottom) had the lowest AICc results. The ANN model showed the least AICc values compared to the other algorithms; the four-parameter models had the lowest, negative AICc values. The optimal combination of four parameters was searched to minimize the AICc value of the ANN model (Fig. 4(c)). The optimal combination for the ANN model was determined as P0, P2, P3, and P5: one headspace meter and three liquid-facing meters excluding the top and the bottom ones (P1 and P7). The same combination resulted in a significant decrease of AICc for the RF model, but comparable or even higher AICc’s for the other two models. These results imply that selecting the parameters is required to optimize the model output for liquid level estimation using the current method. To summarize, the pressure data were essential to building accurate models to estimate the liquid level, while the temperature showed little effect. Among the different levels, the pressure meter located in the headspace is crucial, and the number of sensors in the liquid can be optimized to increase the model accuracy.
4. ConclusionsIn this study, a comparison among four algorithms and various variables was conducted to increase the accuracy of the real-time liquid level estimation method. Both the ANN and RF models showed plausible accuracy, while the MLR and SVM models had higher errors than ANN and RF. ANN and MLR increased their accuracy with more pressure variables. In contrast, RF and SVM performed worse with the increasing number of variables. Variable importance analysis showed that the headspace pressure meter was essential, while the temperature sensor contributed little to the model. The AICc test suggested that using four sensors, including one in the headspace and three in the liquid phase, showed an optimal performance from the current dataset. The sensor combination should be optimized based on the scale and the configuration of the system using ML and statistical techniques like AICc. Overall, ML techniques could significantly improve the estimation model output and optimize the number of pressure sensors. The results of this study can give the insight to plant operators for monitoring the liquid level accurately and in real-time.
AcknowledgmentsThis work was supported by Korea Institute of Energy Technology Evaluation and Planning (KETEP) and the Ministry of Trade, Industry & Energy (No. 20183010092790). The authors also thank Prof. Seo Jin Ki (Gyeongsang National University) for his guidance on the machine learning methods.
NotesAuthor Contributions S.I.Y. (Ph.D. student) conducted all the analyses and wrote the manuscript with input from all authors. C.R. (senior researcher) conducted the experiments and curated the data. K.H.C. (Professor) supervised the analyses and elaborated the discussion. S.G.S. (Associate professor) acquired funding, supervised the project, and revised the manuscript. References1. Shin J, Cho S-K, Lee J, et al. Performance and microbial community dynamics in anaerobic digestion of waste activated sludge: Impact of immigration. Energies. 2019;12:
https://doi.org/10.3390/en12030573
2. Santhosh KV, Joy B, Rao S. Design of an instrument for liquid level measurement and concentration analysis using multi-sensor data fusion. J Sens. 2020;2020:1–13.
https://doi.org/10.1155/2020/4259509
3. Corona F, Mulas M, Haimi H, Sundell L, Heinonen M, Vahala R. Monitoring nitrate concentrations in the denitrifying post-filtration unit of a municipal wastewater treatment plant. J Process Control. 2013;23:158–170.
https://doi.org/10.1016/j.jprocont.2012.09.011
4. Jimenez J, Latrille E, Harmand J, et al. Instrumentation and control of anaerobic digestion processes: a review and some research challenges. Rev Environ Sci Biotechnol. 2015;14:615–648.
https://doi.org/10.1007/s11157-015-9382-6
5. Kawai M, Nagao N, Kawasaki N, Imai A, Toda T. Improvement of COD removal by controlling the substrate degradability during the anaerobic digestion of recalcitrant wastewater. J Environ Manage. 2016;181:838–846.
https://doi.org/10.1016/j.jenvman.2016.06.057
6. Nikolov G, Nikolova B. Virtual techniques for liquid level monitoring using differential pressure sensors. Recent. 2008;9:49–54.
7. Yan P, Gai M, Wang Y, Gao X. Review of soft sensors in anaerobic digestion process. Processes. 2021;9.
https://doi.org/10.3390/pr9081434
8. Rhee C, Yu SI, Kim DW, et al. Density profile modeling for real-time estimation of liquid level in anaerobic digester using multiple pressure meters. Chemosphere. 2021;277:130299.
https://doi.org/10.1016/j.chemosphere.2021.130299
9. Zinatloo-Ajabshir S, Salehi Z, Amiri O, Salavati-Niasari M. Simple fabrication of Pr2Ce2O7 nanostructures via a new and eco-friendly route; a potential electrochemical hydrogen storage material. J Alloys Compd. 2019;791:792–799.
https://doi.org/10.1016/j.jallcom.2019.04.005
10. Hussain MA, Chen Z, Wang R, et al. Landslide susceptibility mapping using machine learning algorithm. Civ Eng J. 2022;8:209–224.
https://doi.org/10.28991/CEJ-2022-08-02-02
11. Jia Y, Hou X, Wang Z, Hu X. Machine learning boosts the design and discovery of nanomaterials. ACS Sustain Chem Eng. 2021:6130–6147.
https://doi.org/10.1021/acssuschemeng.1c00483
12. Zinatloo-Ajabshir S, Baladi M, Salavati-Niasari M. Sono-synthesis of MnWO4 ceramic nanomaterials as highly efficient photocatalysts for the decomposition of toxic pollutants. Ceram Int. 2021;47:30178–30187.
https://doi.org/10.1016/j.ceramint.2021.07.197
13. Mahdavi K, Zinatloo-Ajabshir S, Yousif QA, Salavati-Niasari M. Enhanced photocatalytic degradation of toxic contaminants using Dy2O3-SiO2 ceramic nanostructured materials fabricated by a new, simple and rapid sonochemical approach. Ultrason Sonochem. 2022;82:105892.
https://doi.org/10.1016/j.ultsonch.2021.105892
14. Tabatabaeinejad SM, Zinatloo-Ajabshir S, Amiri O, Salavati-Niasari M. Magnetic Lu2Cu2O5-based ceramic nanostructured materials fabricated by a simple and green approach for an effective photocatalytic degradation of organic contamination. RSC Adv. 2021;11:40100–40111.
https://doi.org/10.1039/d1ra06101a
15. Choi C, Kim J, Han H, Han D, Kim HS. Development of water level prediction models using machine learning in wetlands: A case study of Upo Wetland in South Korea. Water. 2019;12:
https://doi.org/10.3390/w12010093
16. Granata F, Papirio S, Esposito G, Gargano R, De Marinis G. Machine learning algorithms for the forecasting of wastewater quality indicators. Water. 2017;9(2)105.
https://doi.org/10.3390/w9020105
17. Abu Qdais H, Bani Hani K, Shatnawi N. Modeling and optimization of biogas production from a waste digester using artificial neural network and genetic algorithm. Resour Conserv Recycl. 2010;54:359–363.
https://doi.org/10.1016/j.resconrec.2009.08.012
18. Talebkeikhah M, Sadeghtabaghi Z, Shabani M. A comparison of machine learning approaches for prediction of permeability using well log data in the hydrocarbon reservoirs. J Hum Earth Future. 2021;2:82–99.
https://doi.org/10.28991/hef-2021-02-02-01
19. Sujatha A, Govindaraju L, Shivakumar N, Devaraj V. Fuzzy knowledge based system for suitability of soils in airfield applications. Civ Eng J. 2021;7:140–152.
https://doi.org/10.28991/cej-2021-03091643
20. Pérez-Díaz P, Martín-Dorta N, Gutiérrez-García FJ. Construction labour measurement in reinforced concrete floating caissons in maritime ports. Civ Eng J. 2022;8:195–208.
https://doi.org/10.28991/cej-2022-08-02-01
21. Lantz B. Machine learning with R. Packt Publishing; 2013.
https://doi.org/10.1080/10686967.2019.1648086
22. Ray S. A quick review of machine learning algorithms. In : 2019 International Conference on Machine Learning, Big Data, Cloud and Parallel Computing (COMITCon); 14–16 Feb, 2019; IEEE; Faridabad, India: 2019. p. 35–39.
23. Yadav AK, Chandel SS. Solar radiation prediction using Artificial Neural Network techniques: A review. Renew Sust Energ Rev. 2014;33:772–781.
https://doi.org/10.1016/j.rser.2013.08.055
24. Andrade Cruz I, Chuenchart W, Long F, et al. Application of machine learning in anaerobic digestion: Perspectives and challenges. Bioresour Technol. 2022;345:126433.
https://doi.org/10.1016/j.biortech.2021.126433
25. Ben Ishak A. Variable selection using support vector regression and random forests: A comparative study. Intell Data Anal. 2016;20:83–104.
https://doi.org/10.3233/ida-150795
26. Kuhn M. caret: Classification and Regression Training. Available from: https://CRAN.R-project.org/package=caret
27. Gevrey M, Dimopoulos I, Lek S. Review and comparison of methods to study the contribution of variables in artificial neural network models. Ecol Modell. 2003;160:249–264.
https://doi.org/10.1016/s0304-3800(02)00257-0
28. Akaike H. Information theory and an extension of the maximum likelihood principle. Breakthroughs in Statistics. Springer Science+ Business Media; New York: 1998. 1:
https://doi.org/10.1007/978-1-4612-1694-0_15
29. Song E, Won S, Lee W. Using the corrected Akaike’s information criterion for model selection. KJAS. 2017;30:119–133.
https://doi.org/10.5351/kjas.2017.30.1.119
30. Venables WN, Ripley BD. Modern Applied Statistics with S. 4th edSpringer; 2002.
https://doi.org/10.1007/978-0-387-21706-2
31. David E, Rumelhart GEH, Williams Ronal J. Learning representations by backpropagation. Nature. 1986;533–536.
https://doi.org/10.1038/323533a0
32. Shieh Y-Y, Fouladi RT. The effect of multicollinearity on multilevel modeling parameter estimates and standard errors. Educ Psychol Meas. 2016;63:951–985.
https://doi.org/10.1177/0013164403258402
33. Alin A. Multicollinearity. Wiley Interdiscip Rev Comput Stat. 2010;2:370–374.
https://doi.org/10.1002/wics.84
Fig. 2Model fitting results using the temperature and the two (a–d) or seven (e–i) pressure readings as variables. The MLR (a), (f), ANN (b), (g), RF (c), (h), SVM (d), (i) and cubic (e) models are represented. 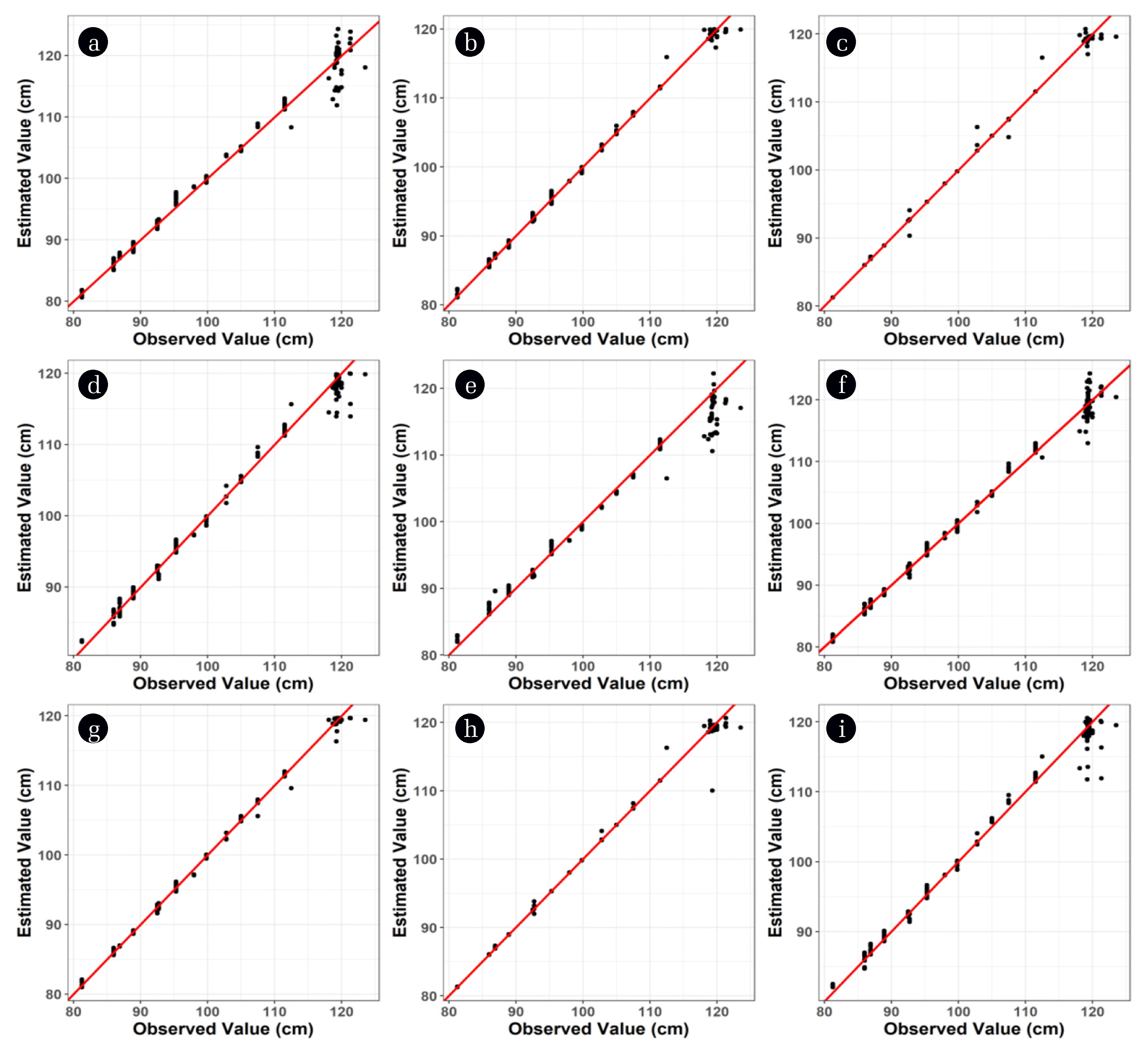
Fig. 3The variable contribution analysis results for the models using the two (a), three (b), or seven (c) pressure readings as variables. 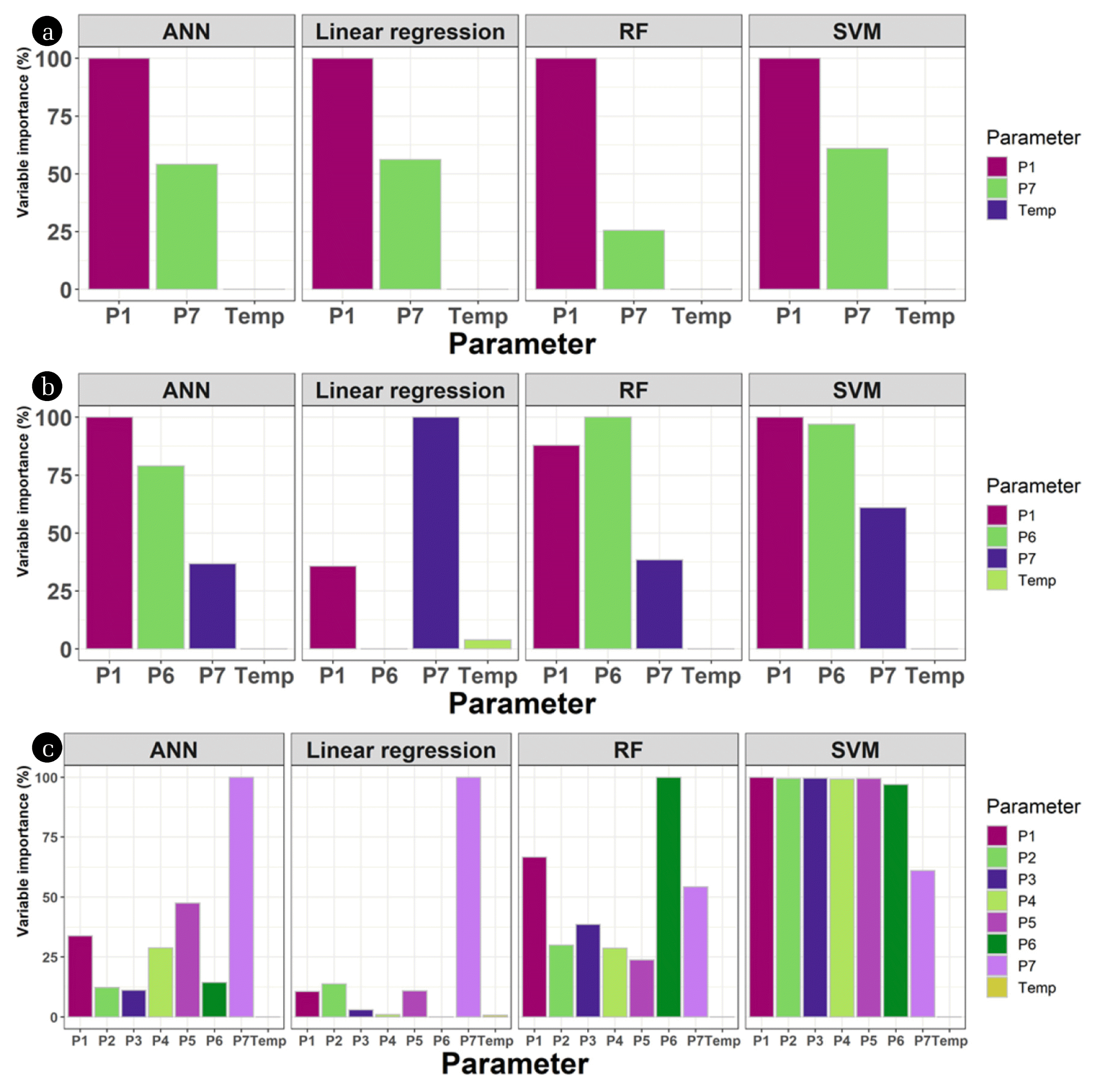
Fig. 4The AICc results when parameters were removed one by one from the bottom layer (a) or the top layer (b); and when an optimized set of parameters were used (c). The number following ‘remain’ means the number of parameters remaining after removing pressure layers. For example, ‘remain: 2’ in (a) has two pressure parameters near the top (i.e., P0 and P1), while ‘remain: 2’ in (b) has two pressure parameters near the bottom (i.e., P6 and P5). In (c), four pressure parameters (P0, P2, P3, and P5) were ‘selected’ to minimize the AICc values of the ANN algorithm, and were compared to the models including all seven (‘full’) pressure parameters. 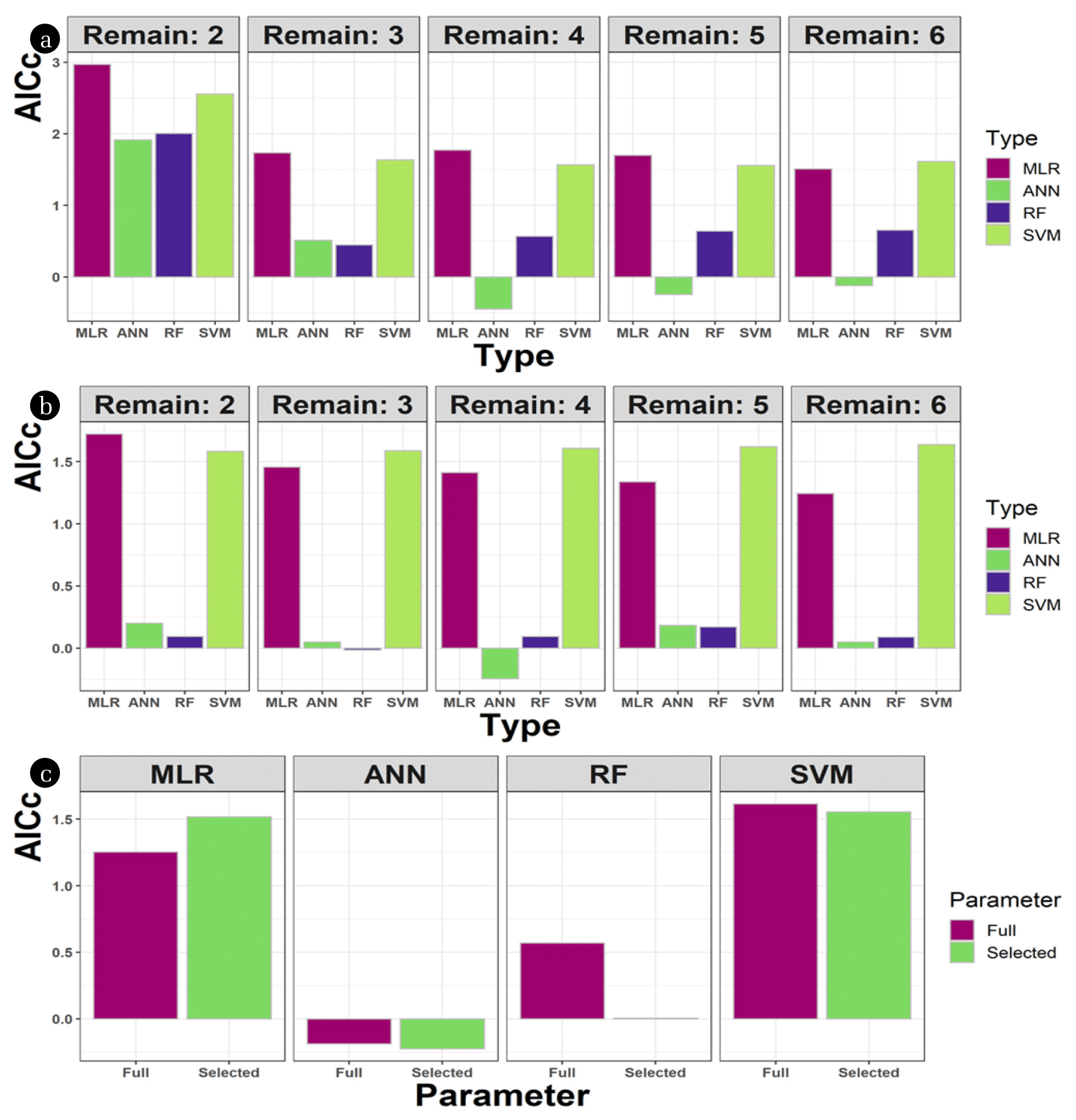
Table 1Performance Indices of the Model Using Two Pressure Readings (i.e., bottom and the headspace)
Table 2Performance Indices of the Model Using All Seven Pressure Readings
Model described in Rhee et al. [8]. Table 3Performance Indices of the RF Models Using Data without Specific Pressure Layers Table 4Performance Indices of the ANN Models Using Data without Specific Pressure Layers |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||