An analytical solution for one-dimensional contaminant transport in a double-layered contaminated soil with imperfect diffusion boundaries
Article information
Abstract
An analytical method is proposed to solve the contaminant transport in a double-layered contaminated soil with imperfect diffusion boundaries. By virtue of the separation of variables scheme, the governing equation for contaminant diffusion is split into two ordinary differential equations, and the corresponding general solutions are obtained. By utilizing the initial, continuity and boundary conditions of the system, and the orthogonality of trigonometric functions, the analytical solution for contaminant concentration in the double-layered contaminated soil is derived, which can be further used to describe the average degree of diffusion. The reliability and accuracy of the developed solution is verified by comparing with the existing analytical solution and numerical simulation results. Selected numerical examples are further presented to analyze the influence of the imperfect diffusion boundaries on the spatial/time distribution of contaminant concentration, average degree of diffusion and mass flux. The results show that greater imperfect diffusion capacity coefficients lead to lower contaminant concentration distribution within the entire depth range and higher average degree of diffusion for a given time. Particularly, it only takes 23.32 years to complete the entire diffusion process when imperfect diffusion capacity coefficients are infinite. The developed solution can provide useful guidance for engineering practice.
1. Introduction
As an economical and effective treatment method, contaminant repository is mainly applied into the disposal of industrial pollution, landfills and tailings, and the stock of various these pollutants is over 2.82 × 1010 ton per year [1]. The engineering problem of the repository as a source of contaminant located below the water source or above the aquifer is one of the most important challenges. Natural weak diffusive clay layer or geosynthetic layer with slight diffusive capabilities is commonly used to cover underwater contaminant sources [2], such as the stratified contaminated soil layer containing a large amount of high-concentration and highly corrosive leachate. It should be pointed out that under the coupling effect of multiple fields, the contaminant source of the repository is likely to diffuse to the adjacent soil and water with great difficulty to repair again, which seriously threatens the environmental health [3–5]. In the above cases, molecular diffusion induced by concentration differences is the key factor for the contaminant diffusion to the adjacent soil or cover layer because of its low hydraulic conductivity of the clay (e.g., < 10−7 cm/s), low leachate head (e.g., < 0.3 m), and small Peclet number [6–9]. Besides, diffusive transport problem comprehensively exists in the engineering materials, such as compacted clay liner [10, 11], underwater cap [12], geosynthetic clay lining [13], and composite liners [14, 15]. In order to prevent and slow down the damage of contaminant on the surrounding environment, it is necessary to study the related problems [16–18] caused by the diffusion of contaminants.
Although the diffusion problem in engineering practice can be analyzed by the numerical simulation schemes [19, 20], analytical methods can provide a deep understanding for the essence of the related problem. In addition, the derived analytical solutions are simple, economical and effective, and they can also be used to validate the complex numerical simulation schemes in which it is difficult to accurately determine the valid parameters [21–23]. For instance, for the preliminary design of a landfill site, most of the valid parameters are difficult to obtain directly, but the analytical solutions can lead to a smooth design [24–27]. Over the past many years, various analytical methods are proposed to solve the contaminant diffusion problem of different types of porous media by supposing different diffusion boundaries and initial conditions. For instance, Foose et al. [14] introduced the Laplace transform to derive the analytical solution of the contaminant diffusion in a double-layered medium considering the semi-infinite boundary, and further used the finite difference method to study the one-dimensional diffusion of the double-layered medium under the assumption of zero-concentration boundary. Shackelford et al. [28] adopted the methodology of transforming the analytical solution of small strain one-dimensional consolidation of saturated compressible porous medium into the solution of one-dimensional liquid-phase diffusion through saturated porous medium under time-dependent boundary and complex initial conditions. Chen et al. [29], Xie et al. [30] proposed the analytical solutions for the one-dimensional diffusion of contaminant in soil considering the boundary of finite thickness and the stratification of soil media. Li et al. [31] established the solute convection-diffusion equation in a double-layered finite depth porous medium, and developed the analytical solutions corresponding to different boundary conditions. It can be observed from the above studies that the description of the boundary is assumed to be an ideal and perfect one.
However, the diffusion from contaminated soil to the adjacent materials are really not the ideal diffusion due to the great difference in the diffusive behaviors between different materials. It is also reported that the damage on the barrier layer and technical defects during construction and operation are inevitable, which increases the corresponding average diffusion capability [32, 33]. Therefore, in order to better portray this kind of complicated problem, the interface between the contaminated soil layers and the adjacent layers could be modeled as the imperfect diffusion boundaries in theory, which motivates the present study.
In this paper, we propose a novel one-dimensional model for the diffusion of contaminants from the double-layered contaminated soil layers to the adjacent capping and bottom natural soil layers with imperfect diffusion boundaries. It is noted that the newly developed imperfect diffusion boundary is used to portrait the imperfect diffusion behavior from the contaminated soil to the adjacent layers. The diffusion equation of contaminant is split into two separate ordinary differential equations using separation of variables method, and the corresponding general solutions are obtained. After substituting the initial conditions, continuity conditions and imperfect boundary conditions of the layered system into the general solutions, and using the orthogonality of trigonometric functions, the analytical solution for the diffusion of contaminant is derived. The developed solutions are verified by comparing with the existing analytical solution and numerical results by the COMSOL Multiphysics software. The influence of the imperfect diffusion boundaries on the spatial/time distribution of contaminant concentration, average degree of diffusion and mass flux are also analyzed in details. The analytical solutions proposed in this paper can be served as the benchmarks for the complicated and powerful numerical solutions and provide useful guidelines for engineering practice.
2. Solution of the Contaminant Transport Problem
2.1. Basic Assumptions and Mathematical Model
The following assumptions are adopted when establishing a one-dimensional contaminant diffusion model from a double-layered contaminated soil to the capping and bottom natural soil layers:
Hydraulic conduction, degradation, convection-dispersion, adsorption retardation, and other transport mode on the concentration of contaminants is not considered as the way of contaminant transport, while the main transport mode of contaminants in the soil is molecular diffusion.
The top and bottom boundaries of the contaminated soils are modelled as imperfect diffusion boundaries. The outlet boundaries of the capping layer and bottom natural soil layer are assumed to be zero concentration, i.e., full diffusion boundary.
Each contaminated soil layer is homogeneous, isotropic and saturated soil, and the corresponding physical properties (e.g., porosity, effective diffusion coefficient, etc.) are assumed to be constants.
The diffusion of contaminants in the contaminated soils is only along the depth direction (i.e., one-dimensional diffusion), and follows Fick’s second law.
The concentration of contaminant and flux are continuous at the interface between two contaminated soil layers.
The contaminants diffusion from the contaminated soils to the top capping layer and the bottom natural soil layer with imperfect diffusion boundaries is illustrated in Fig. 1. A double-layered contaminated soils is over the bottom natural soil layer, and the top capping layer is covered on it to prevent contaminant entering into the water. The thickness of the top cap layer, contaminated soil layers 1 and 2, and the bottom healthy soil layer are denoted by L1, h1, h2 and L2, respectively. The origin of the coordinate is at the top surface of contaminated soil layer 1 with the positive z direction being downwards. The interfaces between the contaminated soil layers and the adjacent layers are modelled as the imperfect boundaries, i.e., the concentration at the boundaries between the contaminated soil layers and the adjacent layers is continuous, but the diffusion rate is discontinuous. With this kind of imperfect boundaries, not only can various soil layers with different diffusion capabilities be handled, but also can be reduced to the classical engineering problems. For instance, when the bottom boundary has zero diffusivity and the top diffusivity is weak, it can be transformed into a boundary condition commonly used in landfill storage problems. When the top and bottom of the contaminated layers are full diffusion boundary, it can be transformed into the boundary condition used for the problem of the contaminated soil diffusing to the adjacent water source.

Diagrammatic sketch for one-dimensional diffusion model of double-layered contaminated soil with imperfect boundaries.
The governing equation for the contaminant diffusion from the double-layered contaminated soil to the adjacent layer can be written as
where Ci(z, t) and Dvi are the concentration and effective diffusion coefficient of contaminant in the ith (i = 1, 2) contaminated soil layer, respectively; For the ith layer, the effective diffusion coefficient Dvi can be further defined as the product of the apparent tortuosity factor τai and the aqueous diffusion coefficient for the solutes D0i i.e., Dvi = D0iτai [31]; z is the spatial coordinate variable along the depth direction, and t is the time variable.
The initial concentration of the contaminant in the contaminated soil layers can be expressed as
where C0 is the initial concentration of contaminant in contaminated soil layers 1 and 2 when t = 0.
Given that the contaminant concentration and flux are continuous at z = h1, hence the following continuity conditions hold
where n1 and n2 are the porosities of the contaminated soil layers 1 and 2, respectively.
The concentration at the boundary between the contaminated soil layers and the adjacent layers is continuous, but the diffusion rate is discontinuous. So the imperfect diffusion boundary conditions at the top surface of contaminated soil layer 1 (i.e., z = 0) and the bottom surface of the contaminated soil layer 2 (i.e., z = H) can be written as
in which
where D1 (L1) and D2 (L2) are, respectively, the effective diffusion coefficients (thickness) of the top capping layer and the bottom natural soil layer; Sd1 and Sd2 are the imperfect diffusion capacity coefficients representing the ratio of the diffusion capacity of the imperfect diffusion layers (i.e., the top capping layer and the bottom natural soil layer).
It is noted that Eq. (5) and Eq. (6) describes the continuity condition of the top and bottom boundaries of the contaminated soil layer, and the boundary concentration is controlled by the imperfect diffusion capacity coefficients Sdi (i = 1, 2). When the capping layer has perfect protective function (ideal condition), it can be considered that it has no ability to diffuse, i.e, Sd1 = 0. However, when the protective function of capping layer is relatively weak, it has certain ability to diffuse, i.e., Sd1 > 0. The above description also applies to the bottom natural soil layer.
2.2. General Solution
2.2.1. Concentration in contaminated soil
According to the separation of variables method, the following single-variable function Ci(z, t) is introduced
Substituting Eq. (8) into Eq. (1) and dividing both sides of the equations by φi(z)θi(t) at the same time results in
Introducing the constant λ, Eq. (9) can be split into two separate ordinary differential equations as
The solutions of Eq. (10) and Eq. (11) can be expressed as
Substituting the initial conditions, continuity conditions and imperfect diffusion boundary conditions given in Eqs. (2)–(6) into Eqs. (12)–(14), and utilizing the orthogonality of trigonometric functions, we have
in which
where λm (m = 1,2,3,…) is the positive root of the following characteristic equation
It is noted that λm in Eq. (19) can be solved using the dichotomization method. Besides, the series in Eq. (15) converge quickly, and the accuracy of the series can be ensured when setting m = 100.
The mass flux in the ith (i = 1, 2) layer caused by diffusion in contaminated soil can be expressed in terms of the first Fick’s law as
where Ji(z, t) is the mass flux in the ith contaminated soil layer.
Substituting Eq. (20) into Eq. (15) results in
2.2.2. Average degree of diffusion
Since the contaminant concentrations in the two contaminated soil layers are derived in the above section, the degree of diffusion of contaminants can be further determined. For the convenience of the following analysis, the average degree of diffusion Da is defined as the ratio of the average concentration diffused to the adjacent layer to its initial concentration as [7].
in which
where Ddi (i = 1, 2) is the average degree of diffusion of contaminant in the ith contaminated soil layer; Da is the average degree of diffusion, which describes the overall degree of diffusion of contaminants in the contaminated soil layers.
It is noted that Sdi = 0 and ∞ (i = 1, 2) are the ideal boundaries, which correspond to the full diffusion and non-diffusion boundaries, respectively. When Sdi are equal to the finite value, the boundaries are really the imperfect boundaries. When Sd1 is equal to 0 and the value of Sd2 represents the diffusion capacity of the boundary between the liner and the contaminated soil layer, the calculation model can be transformed into the corresponding engineering problem in the landfill [11, 13]. When Sd2 is equal to 0 and the value of Sd1 represents the diffusion capacity of the boundary between the capping layer and the contaminated soil layer, the calculation model can be transformed into the engineering problem corresponding to the underwater capping layer [12]. In addition, the diffusion capacity of the boundary layer increases with the increase of Sdi.
3. Results and Discussion
3.1. Verification of the Present Solution
In the past study, Li and Cleall [31] developed general analytical solutions for conservative solute diffusion in one-dimensional double-layered porous media, and analyzed the contaminant diffusion in a reduced single-layer uncapped contaminated sediment with bottom zero-flux boundary. In order to verify the reliability and accuracy of the analytical solution proposed in the present paper, the reduced present solution is compared with this existing solution first. The original parameters used in Li and Cleall [31] are: H = 1.5 m, Dv = 9.4 × 10−10 m2/s, n = 0.45 and retardation factor Rd = 43.3. It is noted that Li and Cleall [31] considered the effect of retardation factor, hence we need to modify Dv as Dv/Rd to keep the same condition. Hence, the input parameters in the present calculation are: h1 = h2 = 0.75 m, Dv1 = Dv2 = 2.1709 × 10−11 m2/s, n1 = n2 = 0.45. For general applications, the normalized contaminant concentration is defined as C* = C/C0, in which C denotes the concentration of contaminant in contaminated layers 1 and 2. Fig. 2 shows the comparison of contaminant concentration vs. normalized depth between the reduced present solution and Li and Cleall’s solution. It can be seen from Fig. 2 that the results from the present solution are very close to those from Li and Cleall [31] for different times.

Variation of normalized contaminant concentration C* with normalized depth z/H. Present solution vs. Li and Cleall’s solution.
To further verify the reliability of the present solution, we compare the present analytical solution with two numerical examples calculated by COMSOL Multiphysics software. The contaminated soil layer and the imperfect diffusion layer system are assumed to be layered porous media with different effective diffusion coefficients in the following calculation. The contaminated soil layers 1 and 2 contain, respectively, ZnSO4 and NaCl contaminant sources with the same initial contaminant concentration. The effective diffusion coefficients of Zn2+ (i.e., Dv1) and Cl− (i.e., Dv2) are employed in the following calculation [35]. Four cases with different combination of Sd1 and Sd2 are: Case 1 with Sd1 = ∞, Sd2 = ∞; Case 2 with Sd1 = ∞, Sd2 = 1; Case 3 with Sd1 = 15, Sd2 = 0; Case 4 with Sd1 = 5, Sd2 = 0. Unless otherwise specified, the basic parameters used in the following calculations (i.e., Fig. 3 to Fig. 8) are: H = 1m, h1 = 0.5 m, Tv = 0.129 or 0.279, C0 = 0.1 mol/L, Dv1 = 3.3 × 10−10 m2/s, Dv2 = 6.8 × 10−10 m2/s, n1 = 0.25, n2 = 0.5. It should be pointed out again that Sdi = 0, ∞ and finite values (i = 1, 2) represent the non-diffusion, full diffusion and imperfect diffusion boundaries.
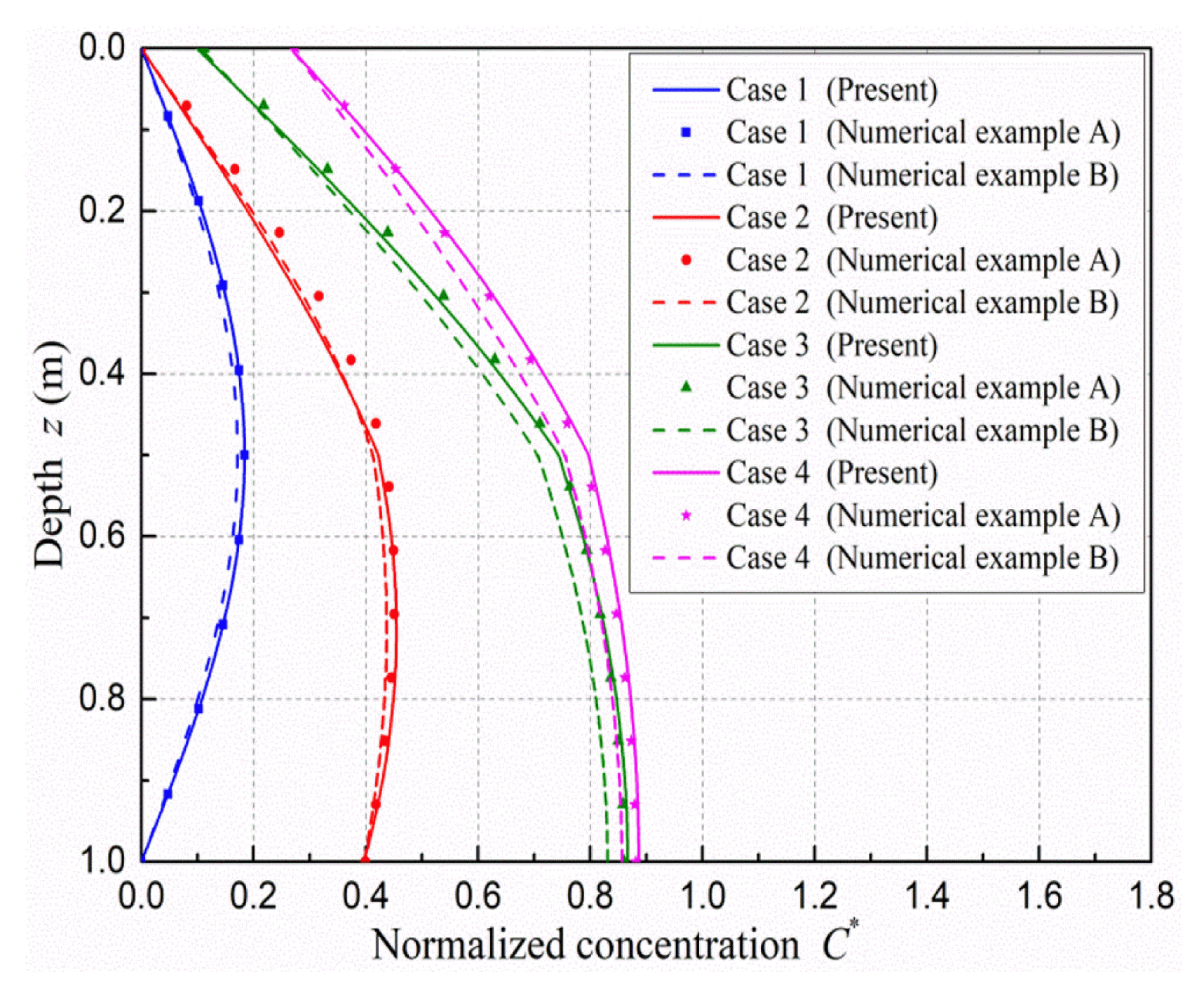
Variation of normalized contaminant concentration C* with depth z. Present solution vs. numerical solution (Tv = 0.279 (i.e., t = 13.0103 years)).

Effect of imperfect diffusion boundaries on the distribution of normalized concentration along depth direction (Tv = 0.129 (i.e., t = 6.0155 years)).

Effect of imperfect diffusion boundaries on the time history of normalized concentration (z = 0.5m).
As for the following numerical simulation, the first numerical example (i.e., numerical example A) corresponds to the same assumption condition with the present analytical solution, and the second numerical example (i.e., numerical example B) further considers the maximum contribution of advection and mechanical dispersion to diffusion-controlled transport. It is noted again that under the condition of low head, permeability coefficient and Peclet number, the transport of contaminant is diffusion-controlled [6–9]. When considering the role of advection and mechanical dispersion in the process of diffusion-controlled transport, the hydrodynamic dispersion coefficient Dri in the ith layer can be defined as [36].
where Dmi is the mechanical dispersion coefficient in the ith layer (i = 1, 2), and it can be defined as Dmi = hivi/10 with hi and vi being the thickness and seepage velocity of the ith layer, respectively.
Darcy flow rate of a double-layered system can be defined as
where Ka is the harmonic average of the permeability coefficient in each layer [36]; Hw and ni are, respectively, the water head height and porosity of the ith layer (i = 1, 2).
To reflect the maximum advection and mechanical dispersion contribution to the diffusion-controlled transport, the critical values of permeability coefficient and water head of each layer are selected with satisfying vihi/Dvi ≤ 1 [37]. The additional selected parameters used in numerical example B are: Hw = 0.3 m, Ka = 1.27 × 10−10 m/s, v1 = 6.6 × 10−10 m/s, v2 = 3.3 × 10−10 m/s.
Fig. 3 shows the comparison of the normalized contaminant concentration distribution along depth direction between the present solution and numerical solution. It can be seen from Fig. 3 that under different working conditions, the results from the present solution generally agree well with those in numerical example A, which further validates the reliability and accuracy of the present solution. It can be also observed from Fig. 3 that molecular diffusion still controls the transport of contaminant in numerical example B. When considering the maximum contribution of advection and mechanical dispersion, the normalized concentration C* in numerical example B is smaller than that in numerical example A. Moreover, as the imperfect diffusion capacity coefficients increases, the convection and mechanical dispersion contributes less to transport of contaminant.
3.2. Influence of Imperfect Diffusion Boundaries
In this section, we mainly analyze the influence of imperfect diffusion boundaries on the contaminant concentration, the average degree of diffusion and mass flux. The influence of the imperfect diffusion boundaries on the distribution of the normalized contaminant concentration distribution along the depth direction is shown in Fig. 4. The behavior of the imperfect diffusion boundaries is presented by the imperfect diffusion capacity coefficients (i.e., Sd1 and Sd2). It can be observed from Fig. 4 that Sdi (i = 1, 2) have great influence on the concentration distribution along the depth direction. When Sdi = 0 (i.e., ideal non-diffusion boundary), the normalized contaminant concentration C* is equal to 1, which means that no contaminant diffuses to the adjacent layer. However, this is very difficult to realize in the engineering practice. When Sdi = ∞ (i.e., ideal full diffusion boundary), the concentrations at z = 0 and H are equal to zero, indicating that the contaminants at the top surface of the contaminated soil layer 1 and at the bottom surface of the contaminated soil layer 2 can freely transport to the top capping and bottom natural soil layers. Hence, in this case (i.e., Sdi = ∞), C* is the smallest when t = 6.0155 years. As Sd1 or Sd2 decreases, C* shows marked increase within the entire depth range. This indicates that the diffusion capacity of the capping and bottom natural soil layers decreases markedly with decreasing Sd1 or Sd2, and more contaminants are kept in the contaminated soil layers. It can be also seen from Fig. 4 that there exists obvious change of curve slope at the interface of two contaminated soil layers. The greater the difference between the values of Sd1 and Sd2, the more obvious the curve slope changes at the interface.
Fig. 5 describes the influence of imperfect diffusion boundaries on the time history of normalized contaminant concentration at a fixed depth. It can be seen from Fig. 5 that when time factor Tv is relatively small, the contaminant concentration at fixed level (i.e., z = 0.5 m) decreases greatly with increasing Sdi, especially when Sdi = ∞. It can be also observed from Fig. 5 that the decreasing ratio of the contaminant concentration in the contaminated soil decreases with increasing time factor. This phenomenon is in accordance with the basic law, i.e., the diffusion velocity of contaminant is affected by the concentration gradient.
Fig. 6 depicts the influence of imperfect diffusion boundaries on the variation of time history of the average degree of diffusion. The x-axis is in a base-10 logarithmic scale. It can be observed from Fig. 6 that the average degree of diffusion Da shows marked increase as time increases. As the time further increases, the changing rate of the average degree of diffusion decreases due to the decrease of the concentration gradient (see the upper four curves in Fig. 6). It can be also seen from Fig. 6 that for a given time, the larger the value of the combination of Sdi, the greater the value of the average degree of diffusion Da. When Sd1 = Sd2 = ∞, the top and bottom surfaces of the contaminated soil layers are ideally full diffusion boundaries, and completing the diffusion process needs only 23.32 years. However, when Sd2 = 0, due to the influence of the ideally non-diffusion boundary of contaminated soil layer 2, the contaminant can only diffuse through the top capping layer. Accordingly, it needs at least 69.95 years to complete the entire diffusion process. It can be concluded from Fig. 4~Fig. 6 that the imperfect diffusion capacity coefficients have great effect on the diffusion of the contaminant. Therefore, in engineering practice, the intrinsic diffusion capacity of the capping layer should be carefully designed for the better environmental conservation.
Fig. 7 and Fig. 8 depict, respectively, the influence of the imperfect diffusion boundaries on the time history of mass flux at z = 0 and z = H level. It can be observed from Fig. 7 and Fig. 8 that the imperfect diffusion boundaries have great influence on the variation of the mass flux with increasing time. In the initial stage of the diffusion (i.e., Tv is relatively small), the mass flux at the top and bottom level of the contaminated soil layers increases with the increase of Sd1 or Sd2. However, when the time factor Tv further increases, the corresponding mass flux decreases with the increase of Sd1 or Sd2. The main reason for this phenomenon is that in the initial stage, the contaminant concentration in the soil decreases quickly for a larger Sd1 or Sd2 value, which induces the decreasing concentration difference in contaminated soil. As a result, when the time is relatively big, the mass flux corresponding to larger Sd1 or Sd2 value is smaller than that corresponding to smaller Sd1 or Sd2 value.
4. Conclusions
In this paper, we propose an analytical method to solve the one-dimensional diffusion of contaminants from the double-layered contaminated soil layers to the adjacent capping and bottom natural soil layers with imperfect diffusion boundaries. At first, the governing equation of contaminant diffusion is split into two ordinary differential equations via the separation of variables method. Then the general solutions for the decoupled ordinary differential equations are obtained. By utilizing the initial conditions, continuity conditions, imperfect boundary conditions of the layered system, and the orthogonality of trigonometric functions, the analytical solution for the contaminant diffusion is finally derived through some algebraic operations. Through the comparison with the existing analytical solution and the numerical solution, the reliability and accuracy of the present solution is validated, and the influence of advection and mechanical dispersion is analyzed. Finally, the influence of the imperfect boundaries (represented by the imperfect diffusion capacity coefficients Sd1 and Sd2) on the spatial/time distribution of contaminant concentration, average degree of diffusion and the mass flux is analyzed. The theory developed in this paper reveals the diffusion mechanism of the contaminant from the double-layered contaminated soil layers to the adjacent layers considering the influence of the imperfect diffusion boundaries, which can provide useful guidance for the engineering practice and could be further served as benchmarks for future numerical solutions. The main conclusions are as follows:
For the diffusion-controlled transport of contaminant, the contribution of advection and mechanical dispersion to the transport process is relatively small. The influence of advection and mechanical dispersion decreases with the increase of imperfect diffusion capacity coefficients Sd1 and Sd2.
Imperfect diffusion capacity coefficients have great influence on the spatial/time distribution of contaminant concentration. As Sd1 or Sd2 decreases, contaminant concentration shows marked increase within the entire depth range for a given time. There also exists obvious change of curve slope at the interface of two contaminated soil layers due to the layering of the soil. When time factor Tv is relatively small, the contaminant concentration at a fixed depth of the contaminated soil layer decreases greatly with increasing Sd1 or Sd2 for a given time.
Imperfect diffusion capacity coefficients Sd1 and Sd2 have great influence on the average degree of diffusion and mass flux. The average degree of diffusion increases with increasing Sd1 or Sd2 for a given time. The mass flux decreases greatly with increasing Sd1 or Sd2 in the initial stage, while it increases with increasing Sd1 or Sd2 when time factor Tv is relatively large.
Nomenclature
C0
Initial concentration of contaminant in contaminated soil layers 1 and 2
Ci
Concentration of contaminant in the ith contaminated soil layer
C*
Normalized concentration of contaminant
D1
Effective diffusion coefficient in capping layer
D2
Effective diffusion coefficient in bottom natural soil layer
Da
Average degree of diffusion
Ddi
Average degree of diffusion of contaminant in the ith contaminated soil layer
Dvi
Effective diffusion coefficient in the ith contaminated soil layer
Ji
Mass flux in the ith contaminated soil layer
ni
Porosities of the ith contaminated soil layer
Sdi
Imperfect diffusion capacity coefficients in ith contaminated soil layer
t
Time variable
Tv
Normalized time factor
Dri
Hydrodynamic dispersion coefficient in the ith contaminated soil layer
Dmi
Mechanical dispersion coefficient in the ith contaminated soil layer
vi
Seepage velocity of the ith contaminated soil layer
va
Darcy flow rate of the double-layered contaminated soil layer system
Ka
Permeability coefficient of the double-layered contaminated soil layer system
Acknowledgment
This research is supported by National Natural Science Foundation of China (No. 52078467).
Notes
Author Contributions
X.L. (Ph.D.) derived the formulations and wrote the manuscript. J.S. (M.S. student) analyzed related literatures and programmed the code. Z.Z. (Ph.D.) reviewed and edited the manuscript. Z.W. (Ph.D.) reviewed and edited the manuscript.



