The fuzzy comprehensive evaluation (FCE) and the principal component analysis (PCA) model simulation and its applications in water quality assessment of Nansi Lake Basin, China
Article information
Abstract
The Fuzzy Comprehensive Evaluation (FCE) and the Principal Component Analysis (PCA) were simulated to assess water quality of the Nansi Lake Basin, China. The membership functions were established via the Nor-Half Sinusoidal Distribution Method, and the weight was calculated via the Exceeding Standard Multiple Method. To enhance the efficiency of extracting principal pollutant, the eigenequation was solved through the Jacobi Method, and the principal components were extracted based on eigenvalue, contribution ratio, accumulating contribution ratio, principal component loading and score. Water quality classification based on “National Surface Water Environmental Quality Standards of China (GB3838-2002) was used to assess the water quality. Considering the difference of the temporal and spatial distribution in average, water quality of Level I was 28.9%, 28.1%, 25.1%, 25.6%, respectively in spring, summer, autumn, and winter, which suggested that water quality in spring and summer was better than in autumn and winter. The order of water quality was Zhaoyang Lake (Level I) > Nanyang Lake (Level I) > Dushan Lake (Level III) > Weishan Lake (Level III and IV). There were four extracted principal components that can replace the fourteen pollutant indexes for assessing water quality. According to the annual mean data of the 1st principal components, the most important pollutions were heavy metals, including As (0.933), Hg (0.931), Cd (0.929), Cr(VI) (0.926), Pb (0.925), and Cu (0.534). It is proved that the combined FCE-PCA model could provide valuable information in the water quality assessment for the Nansi Lake Basin.
1. Introduction
Rivers and lakes play a unique role for societal development through provision (e.g. products and food), support (e.g. wastewater processing and supply of clean water) and enrichment (e.g. aesthetic, recreational and cultural) services. The growing demand for freshwater resources to sustain human activities, coupled with the adverse effects of the same activity, such as the discharge of industrial wastewater and domestic sewage, are likely to cause a crisis in the near future if water resources are not appropriately managed [1, 2]. The shortage of water resources and water pollution is a very serious problem in the arid and semi-arid areas of Northwestern China.
Water quality management involves water quality monitoring, analysis, assessment, and reporting [3, 4]. Water quality assessment is a challenge within the study of the environment. Proper identification of water quality status in a river or lake system based on limited observations is essential for meeting the goals of environmental management [5]. Numerous methods have been proposed in literature to assess water quality, including expert assessment, index assessment, neural networks, and grey clustering [6–8]. Considering that pollution degree of water is a vague concept with inherent imprecision and unclear of classification criteria and the boundaries between different classes of water quality, difficulties of water quality classification and assessment always exist in conventional assessment methodologies such as Water Quality Index (WQI) when describing integrated water quality [9]. Conventional methods for water quality assessment do not consider the uncertainties involved either in measurement of water quality parameters or in the limits provided by regulatory bodies, meanwhile, they also use crisp set and concentration values, which are close to or far from the limits, which are included in the same class [10]. This unclearness has led some environmental researchers to look for advanced assessment methods based on the Fuzzy Comprehensive Evaluation (FCE) and the Principal Component Analysis (PCA).
FCE is designed to interpret the uncertainties of water quality assessment [11]. It comprehensively evaluates the contributions of various pollutants according to predetermined weights, and decreases the fuzziness by using membership functions [12]. Therefore, the sensitivity is higher than other index evaluation techniques [13]. A well designed FCE may be capable of covering the uncertainties in the sampling and analysis process, comparing sampling results to quality standards for each parameter, and summarizing individual parameter values [14]. FCE has been widely used in environmental quality assessment, and has been proven effective in solving problems of fuzzy boundaries and in controlling the effect of monitoring errors [15].
PCA is a multivariate statistical technique used to identify important components or factors that explain most of the variances of a system. It is designed to reduce the number of variables to a small number of indexes while attempting to preserve the relationships present in the original data [16]. In recent years, the PCA model has been applied to a variety of environmental issues, including evaluation of ground water monitoring wells, interpretation of groundwater hydrographs, examination of spatial and temporal patterns of heavy metals contamination and identification of herbicide species related to hydrological conditions [17]. Winter et al. applied the PCA method to investigate the areal distribution of various types of water level fluctuation patterns and to determine if fewer wells could be measured while still achieving effective long-term monitoring goals at four small research sites in the USA, the results showed that the PCA technique was very useful in summarizing information from large data sets to select long-term monitoring wells [18]. Mustapha et al. [19] used the PCA method to assess water quality of the Jakara River Basin; these authors made the contributions to the existing knowledge on the spatial variations of surface water quality and are believed to serve as a baseline data for further studies. Additional, the PCA method has been used to estimate spatial and temporal patterns of heavy metal and organic pollutant, and these results have provided good examples of the effective applications of PCA. However, there are few documented examples of the evaluation of the high dynamic and complex water quality monitoring in river, lake or drainage basin [20]. Therefore, the veracity of water quality assessment for Nansi Lake Basin could be enhanced via the combination between FCE and PCA [21].
The aims of this study are to demonstrate the application of FCE-PCA model to assess the water quality and to extract the principal pollutants of the Nansi Lake Basin, and to evaluate the importance of various water quality parameters. The specific objectives are: (1) to present detailed procedures of FCE-PCA model, (2) to assess the water quality results of the Nansi Lake Basin, and (3) to extract the principal pollutants that are most important in assessing variations in the Nansi Lake Basin water quality.
2. Experimental Design
2.1. Background of the Nansi Lake Basin
The South-to-North Water Diversion Project was put forward by the government of China. Nansi Lake is a buffer lake of the South-to-North Water Diversion Project (east route), so water quality of the Nansi Lake Basin (34°27′N-35°20′N, 116°34′E-117°21′E) has to be better than that of Class III in accordance with the “National Surface Water Environmental Quality Standards of China (Chinese Environmental Protection Agency, GB3838-2002).” The main pollution sources of the Nansi Lake Basin are industrial pollution sources, agricultural pollution sources and domestic pollution sources from three cities residing within the Shandong Province: Zaozhuang, Jining, and Heze [22]. It is important to manage and evaluate the water quality of the Nansi Lake Basin, based on the water quality requirement of the South-to-North Water Diversion Project, because if we do not then the quality of life of the surrounding area and those within its reach will surely diminish. The Nansi Lake Basin is shown in Fig. 1. As the largest shallow freshwater lake in Shandong Province, China, it consists of four sublakes from north to south, Nanyang Lake, Dushan Lake, Zhaoyang Lake, and Weishan Lake, with a whole catchment area of 30.4×103 km2. The total surface area of the lake is 1..2×103 km2 with 126 km in length from north to south and 5–25 km in width from east to west, and the average depth is only 1.46 m [23].
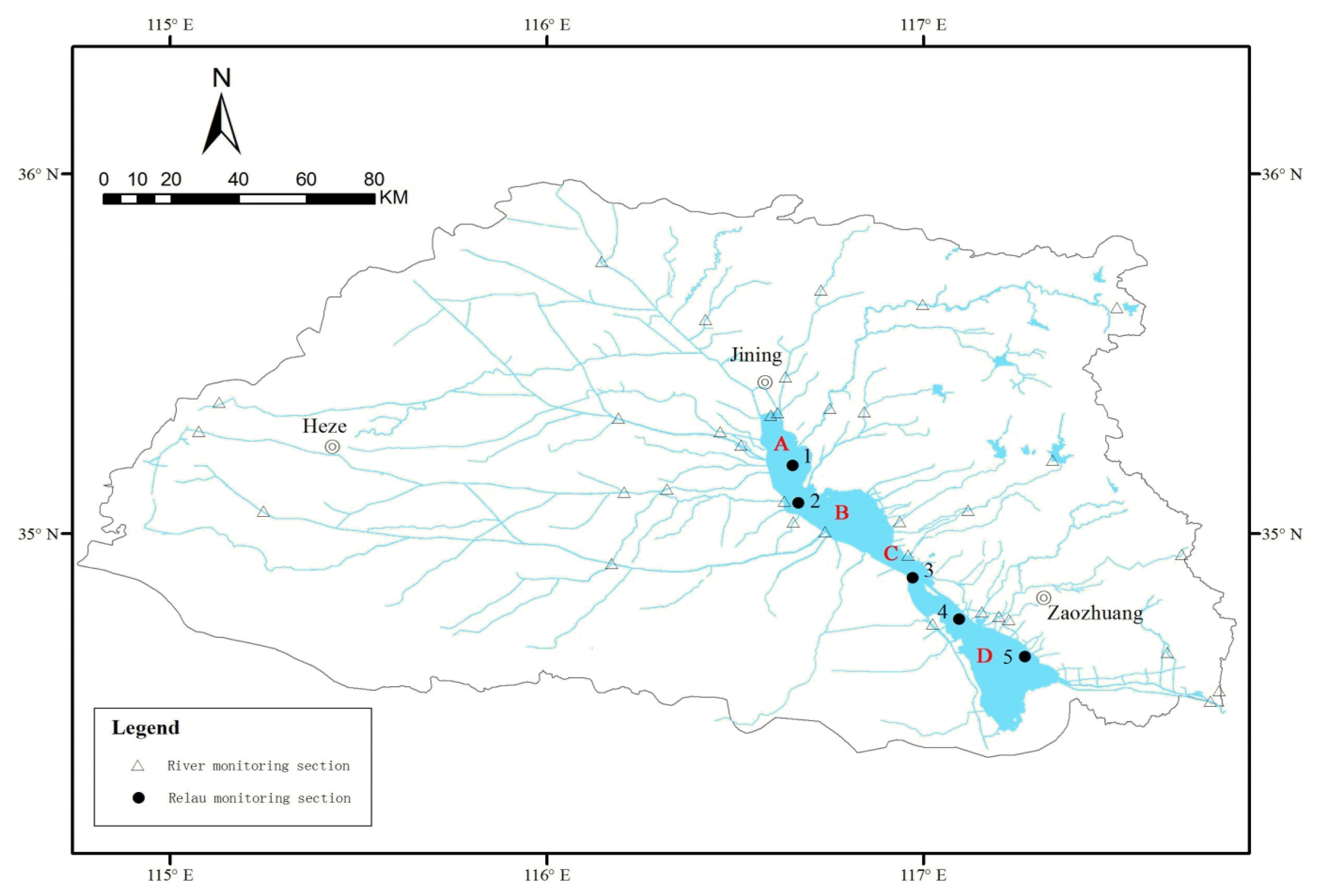
Nansi Lake Basin and Monitoring Sections. △ represent river monitoring section and ● represent relau monitoring section. A: Nanyang sublake; B: Dushan sublake; C: Zhaoyang sublake; D: Weishan sublake.
There are 3.17×104 square kilometers in the Nansi Lake Basin, mainly including Zaozhuang, Jining, and Heze sity. in order to evaluate the water quality of the Nansi Lake Basin, the five monitoring sections (Fig. 1) and the fourteen monitoring indexes were ensured with hydrological and hydraulic, basin environment, pollution sources and land use, and the indexes were estimated from the earlier studies on the point source pollution and water quality variation trends in the Nansi Lake Basin from 2002 to 2012 [24]. The Models were improved for scientific simulation at the same time.
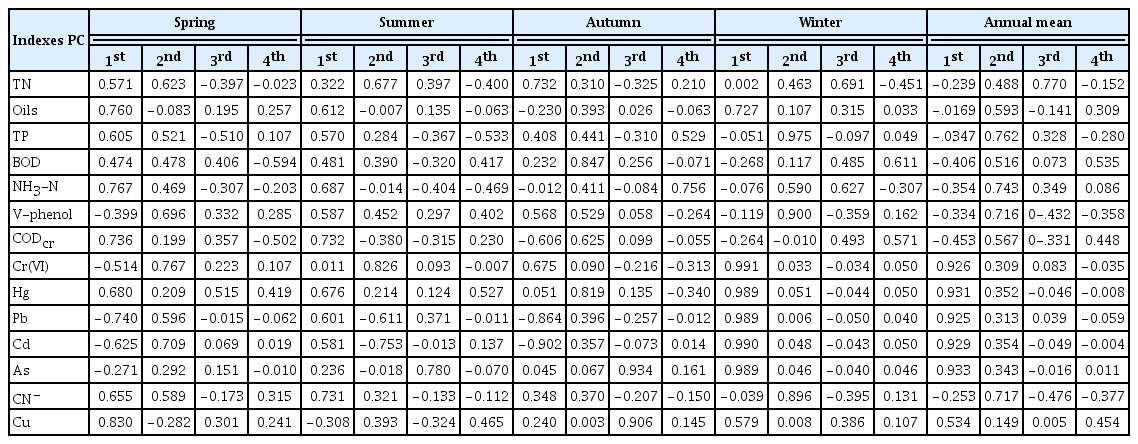
Based on distribution characteristics of industrial enterprise for the Nansi Lake Basin, the fourteen monitoring indexes were selected as assessment parameters to form an assessment factor set U, U={TN, Oils, TP, BOD, NH3-N, V-phenol, CODCr, Cr(VI), Hg, Pb, Cd, As, CN−, Cu}. An assessment criteria set V was also established according to the National Surface Water Environmental Quality Standards of China (Chinese Environmental Protection Agency, GB3838-2002; Table 1).
2.2. The Design of AHP-FCE Model
In the design of the new model for Nansi Lake Basin, the advantages of multi-objective, multi-standard, and structurelessness of AHP were able to avoid one-sidedness and inconsistency resulting from environmental risk identification and evaluation index system. Due to the complexity of environmental risk, fuzzy demarcation, and difficulty in describing accurate scales, secondary-level FCE was designed to achieve comprehensive dynamic grading evaluation of environment risk. Further, the comprehensive dynamic risk classification evaluation methods were realized based on the AHP-FCE model.
According to the characteristics of the hazard installations at Nansi Lake Basin, factors that would affect evaluation results include: a risk source factor, an environmental factor, a human factor, and a preventing ability factor (Fig. 2). Fourteen specific solution hierarchy factors are also listed.
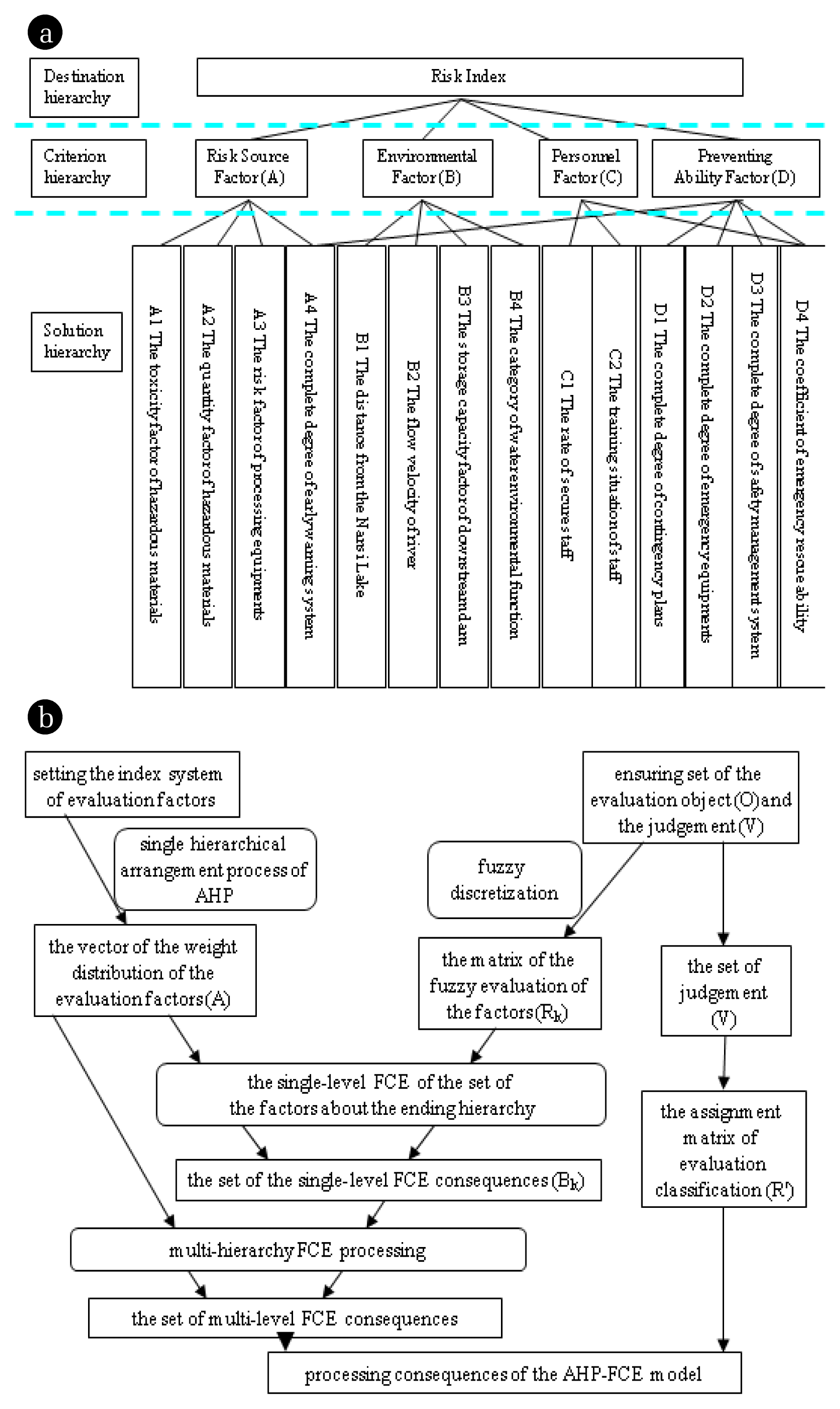
The design of AHP-FCE model for Nansi Lake Basin. (a) The structure of environmental hazard identification and evaluation system. (b) The processing of AHP-FCE model.
The risk index evaluation system and method system was constructed based on risk source and industrial characteristics, basin characteristics of the hydrological and hydraulic, and a consideration of the terrain of Nansi Lake Basin, site of risk source, developing process of risk, and the controlling process of risk.
2.3. Model Description
Simple fuzzy classification (SFC), fuzzy similarity method (FSM) and FCE are all subtitles of fuzzy synthetic evaluation (FSE). FCE has been used recently by a number of researchers in various environmental areas [25]. Since 1965, when the FCE model was first put forward by L.A. Zadeh with Fuzzy Set, fuzzy mathematics has become an indispensable part of mathematical science and has been widely used in social and natural science fields, including psychics, autocontrol, bioengineering and environmental science [26, 27]. Based on the complexity and uncertainty of water body environment, the fuzzification of water quality grade and water quality standard, William Silver was the first to assess seawater environment via fuzzy mathematics theory [28]. Following his lead, domestic and overseas scholars began evaluating water environment quality with the usage of the FCE model.
The PCA model practically transforms the original data matrix into a product of two matrices, one of which contains the information about the samples and the other about the variables. The principle components are the uncorrelated variables obtained by multiplying original correlated variables with eigenvector and are weighted linear combinations of the original variables. That is to say that the PCA model provides information on the most meaningful parameters, which describe whole data set affording data reduction with minimum loss of the original information. The PCA model has been widely used in water quality assessment of rivers, diggings, underground water reservoirs and lakes [29].
2.2.1. Fuzzy comprehensive evaluation model
The following procedure describes the FCE model.
(a) Select assessment parameters and establish assessment criteria: It is crucial to select representative, rational, and accurate water quality assessment parameters to form an assessment factor set U based on the actual local situation. This is expressed as
where n is the number of selected assessment parameters. The assessment criteria set V is established from National Surface Water Environmental Quality Standards of China. This is expressed as
where m is the number of assessment criteria categories.
The weights set A is established with different degree of importance. This is expressed as
(b) Single-factor fuzzy evaluation: Single-factor fuzzy evaluation is defined as ensuring the membership between the evaluation object and the assessment criteria set Vj based on the ith factor ui. The single-factor fuzzy evaluation set Ri is expressed as
Thus, the single-factor fuzzy evaluation sets of all factors can be obtained as follows:
Based on the above single-factor fuzzy evaluation set, the single-factor fuzzy evaluation matrix R is expressed as
where rij (i = 1, 2, …, n; j = 1, 2, …, m) is the membership degree of the ith assessment parameter at the jth level.
(c) Fuzzy Comprehensive Evaluation: Based on single-factor fuzzy evaluation lack of the interaction between evaluation factors and evaluation object, the omnibus evaluation set B is expressed as
where ith row is the influence extent between ith factor and all evaluation factors, and jth column is the influence extent between jth factor and all evaluation factors. The results can reasonably represent the comprehensive influence of all factors.
2.2.2. Principal component analysis model
The following procedure describes the PCA model.
(a) Establish original data matrix X: The original data matrix X is expressed as
where m is the sample number, and n is factor number. To eliminate the influence of dimension and order of magnitudes, the original data matrix X was normalized via the Z-Score Method. The normalization is expressed as
where
(b) Compute correlation coefficient and correlation coefficient matrix: Rij is the correlation coefficient between Xi and Xj, and it is expressed as
Then, the correlation coefficient matrix R is as following:
(c) Solve eigenvalue and eigenvector: The eigenequation |λI – R| = 0 is solved by using the Jacobi Method, and eigenvalue λ is sorted according to the size as λ1 ≥ λ2 ≥···≥ λp ≥ 0.
(d) Compute contribution ratio (CR) and accumulating contribution ratio (ACR), and determine principal component: The CR and ACR are expressed as
In general, when the ACR of eigenvalue is greater than 70%, the corresponding pollutants are defined as principal components and shown as the 1st, 2nd, 3rd, ..., mth (m≥4) principal components.
(e) Compute loading and score of principal component: The loading of principal component is expressed as
Then, the Principal Component Score Matrix Z shows as following:
(f) Determine expression of principal component and comprehensive evaluation function: The expression of principal component is expressed as
And the expression of comprehensive evaluation function is expressed as
According to the circumstance of the Nansi Lake Basin, The FCE-PCA model had been improved and applied to assess the water quality.
3. Results and Discussion
3.1. Model Simulations
The membership functions represent the degree to which the specified concentration belongs to the fuzzy set. The smaller monitoring index is, the better the water quality is, and when the data is close to the critical value, the water quality will be terrible suddenly. Meanwhile, as the response relationship between water quality and monitoring index accords with the Nor-Half Sinusoidal Distribution Function, the membership functions were established via the Nor-Half Sinusoidal Distribution Method as follows.
where X is the actual monitoring data for the ith assessment parameter, and Xj is the criteria value of the ith assessment parameter at the jth level (i = 1, 2, …, n; j = 1, 2, …, m).
Weight was calculated via the Exceeding Standard Multiple Method as follows:
where X is the real concentration of ith pollutant parameter, S is the standard concentration of ith pollutant parameter, Xj is the standard values of jth water quality, and n is the water quality class. The normalization of Wi is expressed as
After normalization, the weight set A was obtained. Water quality data of five relau monitoring sections in spring, summer, autumn, winter and annual mean were analyzed and calculated by the according membership function. The membership degree was calculated by because it is relevant to the weight of water quality indexes. Through the setting of assessment factor set, the building of the assessment criteria set, the membership function, and the weight set, the computational procedure can be realized.
To eliminate the influence of dimension and magnitudes about pollutant indexes, the original data was operated under normalization via SPSS 19.0. The correlation coefficient matrix can be obtained according to the normalization data. The absolute value of the correlation coefficient between any two indexes is usually greater than 0.1 and it is shown that the PCA model can be used to analyze the inter-indexes correlation. The eigenroot, eigenvector, CR and ACR were computed through the use of this correlation coefficient matrix.
3.2. Calculation Results via the FCE-PCA Model
The rivers of the Nansi Lake Basin are seasonal rivers and the water quality of the Nansi Lake Basin is discrepant in different seasons. The principal pollutants should be paid close attention to and the corresponding measure should be taken in the Nansi Lake Basin. The FCE-PCA model was designed according to conditions of the Nansi Lake Basin and the result would be useful for the water environment management. The water quality of five relau monitoring sections was tested in four seasons.
Through analyzing water quality data of five relau monitoring sections by the FCE model, the seasonal and annual water quality results were obtained as follows in Table 2.
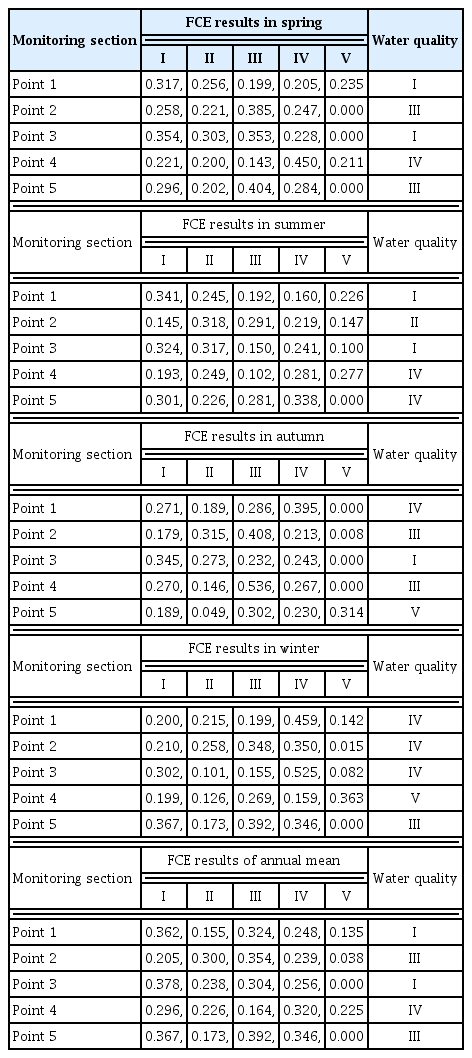
Water Quality Results of FCE Results (a) in Spring, (b) in Summer, (c) in Autumn, (D) in Winter and (E) FCE Results of Annual Mean
The results showed that the annual water quality was relatively good: two monitoring sections (Nanyang sublake-point 1 and Zhaoyang sublake-point 3) belonged to class I (best level), two monitoring sections (Dushan sublake-point 2 and Weishan sublake-point 5) belonged to class III (normal level), and the rest one monitoring sections (point 4 close to Weishan sublake) belonged to class IV (bad level). Small amounts of water in winter and more pollution sources near point 4 have the main effects on the annual water quality. The results also indicated that 80% of the monitoring sections were either superior to or flatting to class III (normal level) in spring, 60% of the monitoring sections were superior to class III in summer, 60% of the monitoring sections were either superior to or flatting to class III in autumn, 20% of the monitoring sections belonged to class III in winter, and 80% of the monitoring sections were either superior to or flatting to class III in annual mean.
The eigenvalue, principal component, contribution ratio and accumulating contribution ratio were computed by the PCA model and the results expressed in Fig. 3.
The eigenroot of the 1st principal component in spring was 5.640, and the contribution ratio was 40.289%. The eigenroot of the 1st principal component in summer was 4.226, and the contribution ratio was 30.184%. The eigenroot of the 1st principal component in autumn was 3.698, and the contribution ratio was 26.416%. The eigenroot of the 1st principal component in winter was 5.927, and the contribution ratio was 42.336%. The eigenroot of the 1st principal component in the annual mean was 5.477, and the contribution ratio was 39.118%.
In the operating procedure of extracting principal component loading, the results were expressed in Table 3.
The related indexes of the 1st principal component were As (0.933), Hg (0.931), Cd (0.929), Cr(VI) (0.926), Pb (0.925), and Cu (0.534) in the annual mean, and the 2nd principal component were TP(0.762), NH3-N(0.743), CN−(0.717), V-phenol(0.716), Oils(0.593), CODCr(0.567), BOD(0.516), and the 3rd principal component were TN(0.770), and the 4th principal component were BOD(0.535). The related indexes of 1st principal component were Cu (0.830), NH3-N (0.767), Oils (0.760), Pb (−0.740), CODCr (0.736), Hg (0.680), and CN− (0.655) in spring. The related indexes of the 1st principal component were CODCr (0.732), CN−(0.731), NH3-N (0.687), Hg (0.676), Oils (0.612), and V-phenol (0.587) in summer. The related indexes of the 1st principal component were Cd (−0.902), Pb (−0.864), TN (0.732), Cr(VI) (0.675), and V-phenol (0.568) in autumn. The related indexes of the 1st principal component were Cr (VI) (0.991), Cd (0.990), Hg (0.989), Pb (0.989), As (0.989), Oils (0.727), and Cu (0.579) in winter.
3.3. Water Quality Assessment and Principal Pollutant Evaluation
The FCE model was used to assess the integrated water quality of the Nansi Lake Basin. In accordance with the water quality changing with seasons, the water quality in the spring and summer was relatively good, but in the winter the water quality was relatively bad. The water quality order of the Nansi Lake Basin is as follows: Zhaoyang Lake > Nanyang Lake > Dushan Lake > Weishan Lake. These results were calculated by FCE model and were similar to Wu Zhouhu [30]. After analyzing the water quality via the FCE model, the next task was to extract the principal pollutants via the PCA model.
There were four principal components extracted via the PCA model, where the accumulating contribution ratio reached 84.634%, 74.533%, 73.032%, 86.085%, and 85.365% in spring, summer, autumn, winter, and annual mean, respectively. The four principal components extracted via the PCA model can replace the fourteen pollutant indexes for assessing water quality. These results show that the combined pollution of heavy metals, toxic pollutants and organic pollutants should be given much more attention in regards towards the Nansi Lake basin; these pollutants are Cd, Pb, Cr(VI), Hg, As, Cu, CN−, V-phenol, Oils, CODCr and BOD. Furthermore, the water eutrophication should be given attention, especially towards TN, NH3-N and TP.
Enhancing the capacity to understand and control water environmental pollution is a critical issue not only in China and the Nansi Lake Basin, but also in other areas around the world. Brömssen et al. [31] assessed the sustainability of low-arsenic aquifers as a safe drinking water source in southeastern Bangladesh, and illustrated the effects of high-arsenic groundwater on human health based on model analysis. In facts, The FCE-PCA model simulation is not only capable of supporting the regulation and evaluation of water quality effectively and scientifically, but will be able to further assist in finding principal components for targeted control of water pollution. PCA model has been used to reduce the number of environmental variables to abstain from multicollinearity [32]. It is reported that principal components for targeted pollution control of the Bouhamdane River, Guelma (north-east Algerian) are evaluated using PCA to realize the water basin management [33].
Besides the understanding of aquatic pollution using the FCE-PCA model, this model method is also used in the fields related to land use [34], and material research [35], which suggested the great potential of the FCE-PCA model in dealing with different problems. In future research, the accuracy and applicability of the combined FCE-PCA should be enhanced, allowing the index and method to function to its full potential by optimizing and by detailing more.
3.4. Environment Implications
To achieve the South-to-North Water Diversion Project and ensure the water quality safety of the Nansi Lake Basin, it is essential to evaluate the water quality and decide the key pollutants. The paroxysmal and gradual warning index of water environment based on the combined FCE-PCA model was structured to ensure the water quality safety of the Nansi Lake Basin and .the South-to-North Water Diversion Project. Results indicated that the heavy metal and organic pollutants may cause some degree environmental risk, and the prevention and control system of risk should pay attention to pollutants (Cu, Cr(VI), Pb, As, V-phenol, Oils, COD) and its sources (paper, chemical, coal mining, operation, textile, etc.). It is the hope that the combined FCE-PCA model will provide valuable information to assess the water quality for the Nansi Lake Basin and the East Route of South-to-North Water Diversion Project.
4. Conclusions
The FCE-PCA model had been applied to assess the water quality of the Nansi Lake Basin in this paper. Based on the analysis of fourteen monitor indexes of the five relau monitoring sections, the water quality classification of the Nansi Lake Basin was determined via the FCE model. The annual water quality was relatively good, with 40% of the monitoring sections belonging to class I (best level), 40% of the sections belonging to class III (normal level), and only 20% of the sections belonging to class IV (bad level). Considering the difference of the temporal and spatial distribution in average, water quality of Level I was 28.9%, 28.1%, 25.1%, 25.6%, respectively in spring, summer, autumn, and winter, which suggested that water quality in spring and summer was better than in autumn and winter. Lastly, the order of water quality was Zhaoyang Lake > Nanyang Lake > Dushan Lake > Weishan Lake.
Based on the analysis of fourteen monitoring indexes of forty-one monitoring sections, the principal pollutants of the Nansi Lake Basin was extracted via the PCA model. There were four extracted principal components that can replace the fourteen pollutant indexes for assessing water quality for the Nansi Lake Basin. Through analyzing the annual mean data, the 1st principal components were heavy metals (e.g. As, Hg, Cd, Cr (VI), Pb etc.), the 2nd principal components were organic and toxic pollutants (e.g., V-phenol, Oils, CODCr, CN− etc.), the 3rd and 4th principal components were TN and BOD.
In conclusion, the water quality of Nansi Lake Basin was relatively good especially in spring and summer, and the key pollution indicators are CODCr, V-phenol, TN, TP, CN−, Hg, As, Cd, Cr, and Pb. The water quality assessment should be chosen from more comprehensive indexes and a more reasonable weight calculation method like the methods found in the FCE-PCA model. It is our hope that the combined FCE-PCA model will explain the discrepancies, enhance the efficiency and goodness-of-fit, and predict power and robustness.
Acknowledgment
This work was financially supported by the National Natural Science Foundation of China (41672340), the Project of Shandong Province Environmental Protection Bureau (NO. SDHBPJ-ZB-09) and China National Key Program for Water Pollution Control (NO. 2009ZX07210-007). The authors would like to thank Jameson Kwan for polishing the English of the manuscript.
Notes
Author Contributions
S.X. (Professor) wrote and revised the manuscript, C.Y. (M.S. student) analyzed the data. Y.C (M.S. student) conducted the experiments. S.W. (Ph.D.), W.D. (Ph.D.), L.H. (Ph.D.) and L.H (Professor) made the model analysis. C.L. (Professor) revised the manuscript. Z.R. (Professor) and W.W (Professor) organized project and revised the manuscript.