Runoff estimation using modified adaptive neuro-fuzzy inference system
Article information
Abstract
Rainfall-Runoff modeling plays a crucial role in various aspects of water resource management. It helps significantly in resolving the issues related to flood control, protection of agricultural lands, etc. Various Machine learning and statistical-based algorithms have been used for this purpose. These techniques resulted in outcomes with an acceptable rate of success. One of the pertinent machine learning algorithms namely Adaptive Neuro Fuzzy Inference System (ANFIS) has been reported to be a very effective tool for the purpose. However, the computational complexity of ANFIS is a major hindrance in its application. In this paper, we resolved this problem of ANFIS by incorporating one of the evolutionary algorithms known as Particle Swarm Optimization (PSO) which was used in estimating the parameters pertaining to ANFIS. The results of the modified ANFIS were found to be satisfactory. The performance of this modified ANFIS is then compared with conventional ANFIS and another popular statistical modeling technique namely ARIMA model with respect to the forecasting of runoff. In the present investigation, it was found that proposed PSO-ANFIS performed better than ARIMA and conventional ANFIS with respect to the prediction accuracy of runoff.
1. Introduction
In hydrology, the rainfall-runoff relationship is considered to be one of the most complicated processes. It is influenced by several factors such as topography, climate, rainfall, etc. Various modeling techniques are used to represent this complex relationship. Available modeling techniques are often grouped into one of the three categories viz. (i) Empirical model, (ii) Conceptual model and (iii) Physically based model. Empirical models are built solely upon analysis of existing data and hence commonly known as a data-driven model. Conceptual models use semi-empirical equations in the model building process and the required parameters are acquired through physical data collection and model calibration process. Physically based models, on the other hand, provide a more realistic approach to modeling by representing the real phenomenon mathematically. Although, physically based models seem more appropriate for modeling purpose but lacks acceptability due to the inherent complexity and computational expense. As a result, empirical modeling techniques such as Autoregressive Integrated Moving Average (ARIMA), Fuzzy inference system (ANFIS), Artificial Neural Network (ANN) models, etc. have gained popularity over the years.
ARIMA belongs to the class of statistical modeling techniques, primarily used for analysis and forecasting of time series data. The biggest advantage of ARIMA is its ability to withstand the nature of underlying data fluctuations. It has been successfully used in modeling various hydrological events [1]. Machine learning techniques such as ANN, FIS are also reported to be efficient in modeling such complex phenomena. Being simple and their ability to handle nonlinearity without the knowledge of the actual system makes them very special among others. Numerous evidences are available in the literature where fuzzy logic (FL) based systems excelled in modeling various hydrological events such as rainfall, runoff, streamflow, etc. [2–5]. The presence of uncertainties and imprecision in these domains make FL based systems a suitable candidate for modeling purpose.
Recent developments have also witnessed an increasing trend in the application of ANN in simulation and prediction of nonlinear problems. ANNs have the advantages of being fault-tolerant, robust in dealing with nonlinearity and possesses learning capability as well. However, its training process often suffers from limitations such as slow learning speed, risk of trapping into local minima, etc. To overcome these problems, various optimization techniques especially PSO based techniques have been used in the past. Asadnia et al. [6] investigated an improved PSO based ANN model to estimate the water level for Heshui Watershed in China. The performance of the PSO-ANN model is then compared with ANNs trained using the conjugate gradient, gradient descent (GD), and Levenberg-Marquardt (LM) neural network algorithms. The results indicate that, in both the cases of a single parameter (rainfall) and multiparameter (rainfall and water level) input, PSO based ANN model achieved the better root mean square error (RMSE) and outperformed conventional ANNs in predicting the low and peak water levels. Cheng et al. [7] investigated Quantum-behaved Particle Swarm Optimization (QPSO) based ANN for generating daily reservoir runoff forecast for the Hongjiadu reservoir in Wu River of China. Authors replaced the conventional training process of ANN with QPSO in optimizing different hyperparameters. The experimental results showed that the QPSO-ANN model could achieve better forecast accuracy compared to the classical ANN model. In another experiment, M. Motahari and H. Mazandaranizadeh presented a comparison of ANN models developed using the LM training algorithm and PSO-ANN model in predicting rainfall-runoff response [8]. The results also revealed that the PSO based ANN model performed better than the conventional ANN model. Although there is no doubt about the ANN’s versatility, but they only provide a black box view of the real system and hence fail to provide the rationale behind a particular model outcome [9]. The same is the case with fuzzy rule-based systems. These systems do not have any definite method to find out the required number of fuzzy rules and the number of membership functions (MF) associated with each rule [10]. Moreover, they don’t have any learning algorithm either for refining MF which can minimize the output error.
ANFIS is a hybrid model that mixes the characteristics of both FL and ANN into one powerful unit which has the advantages of i.e., adaptability, quick convergence, and high accuracy. Moreover, the resultant network does not remain black box anymore as the model would have if–then–else rules to explain the linguistic variables [11]. Over the years, this technique established itself as a useful modeling technique in various hydrological fields. ANFIS was found to be superior in predicting various water resources aspects such as water quality, river flow, flood forecasting, sediment concentration, etc. [12–16]. All these instances among many other applications of ANFIS explain why it has been a popular choice of modeling over the years.
However, recent investigations indicate that ANFIS is a computationally expensive and complex system [17]. It suffers from the inability to handle long term dependencies due to the presence of exploding or vanishing gradient problem [18]. Its training and hyperparameter training process are also found to be very complex. To overcome these problems, researchers have used various optimizing techniques in estimating ANFIS’s parameters. Dariane and Azimi developed a streamflow forecasting model by incorporating a Genetic Algorithm (GA) with conventional ANFIS [19]. The authors reported significant improvement in the model performance when GA selection was applied. Qasem et al. [20] experimented with the conventional ANFIS model by incorporating Differential Evolution (DE), GA and PSO in optimizing trainable ANFIS parameters. The study presented three hybrid ANFIS versions i.e. DE-ANFIS, GA-ANFIS, and PSO-ANFIS for estimating sediment transport in open channels. It was found that modified ANFIS was able to achieve better R2 and RMSE value compared to its original counterpart. Pousinho et al. [21] used a hybridized PSO-ANFIS technique to predict wind power and compared the model’s performance with ARIMA, feed forward neural network, Neural Network with wavelet transform, and wavelet neuro fuzzy model. JalalKamali employed two modified variants of ANFIS namely ANFIS-GA and ANFIS-PSO for predicting groundwater quality of Kerman province, Iran [22]. Basser et al. [23] used a similar ANFIS-PSO based model for estimating the optimal parameters of a protective spur dike. Kisi et al. [24–25] experimented with the ANFIS model by incorporating PSO and DE algorithms for parameter estimation process and showed that modified ANFIS possesses the improved capability of predicting ground-water quality compared to the conventional counterpart. Yosefvand et al. [26] employed a hybrid method based on the ANFIS and PSO for estimating the minimum velocity required for preventing the sedimentation process. Similarly, in another study by Dieu et. al. [27] performed the fusion of ANFIS with cultural (ANFIS-CA), bees (ANFIS-BA) and invasive weed optimization (ANFIS-IWO) algorithms for flood susceptibility mapping. It was found that all three modified versions were capable of finding the optimal model parameters and also succeeded in avoiding the problems of trapping into local minimum. There are numerous other instances available where ANFIS’s parameters were estimated using the heuristic optimization technique [28–29].
From the available literature, it can be observed that in most of the cases, ANFIS showed acceptable performance in predicting various environmental phenomena. However, its performance varied depending on the choice of appropriate model parameters. Various optimization approaches such as evolutionary computing techniques are commonly used for this purpose. These fusions have not only helped ANFIS in achieving a better result but also helped with its faster convergence. This paper presents an attempt to hybridize ANFIS with popular metaheuristic based optimization technique known as particle swarm optimization (PSO) in modeling rainfall-runoff relationship. To the best of our knowledge, the combination of PSO-ANFIS was not been employed for this purpose by any previous researchers. The objectives of the present study are as follows:
To build a fuzzy-neural network based time-series estimation model for estimating rainfall-runoff relationship.
To explore the scope of improving the performance of the conventional ANFIS model by incorporating PSO technique.
To compare the performance of PSO-ANFIS with that of ARIMA model and conventional ANFIS to determine its applicability in the rainfall-runoff estimation process.
The organization of this paper is covered in six different sections. Section 2 introduces a brief discussion about various modeling techniques used in this investigation. Section 3 brings out the discussion about the methodology used in this experiment. This section includes detailed discussion about the study area, input data selection techniques, performance criteria, and model development process. The experimental result and discussion are provided in section 4 and section 5, respectively. Finally, Section 6 presents the conclusion.
2. Models Used
2.1. Adaptive Neuro-ANFIS
ANFIS was originally proposed by Jang [10] in the year 1993. Since then, it has been used in different fields for modeling purposes. The internal structure of ANFIS can be divided into antecedent and the consequent part. These two halves are interconnected with each other by rules in a network form. ANFIS, in its initial phase, discovers the fuzzy rules from the given set of input-output data and then in the later phase applies a neural network to refine those rules. A typical Takagi-Sugeno’s ruleset with two inputs x, y, and one output Z can be defined by:
Where α, β and r represent the linear output parameters. The corresponding ANFIS structure is shown in Fig. 1. It has five layers with two kinds of nodes, represented by circle and square. The square node is referred to as the adaptive node which accepts parameters. The circle node is known as the fixed node and it does not accept any parameter.
Layer 1
The first layer is a fuzzification layer. It maps a crisp input to its corresponding linguistic levels (e.g. good, bad and average) based on the calculation of fuzzy membership function. It can be defined by:
Here, x and y represent the input to the ith node. Usually a bell-shaped membership function such as Gaussian function is used for this purpose. The Gaussian membership function (GMF) can be defined as:
Where a, b and c form the set of adaptable parameters. Values of these parameters actually determine the type of membership function used (e.g. bell-shaped, triangular etc.). These parameters are also referred to as premise parameters.
Layer 2
This layer is also referred to as rules layer. It calculates the strength of incoming signals received from the previous layers. Usually a T-norm operator (multiplication) is used to get the output. The operation can be defined as:
Layer 3
It is known as the normalization layer. Every nodes of this layer computes the ratio of its own rule firing strength to the sum of all others. The output of this layer can be defined by:
Layer 4
This layer is known as the defuzzification layer. The output of layer 4 can be defined as:
Where w̄ is the output of the Layer 3 and {α, β, r} forms a parameter set known as consequent parameters.
Layer 5
The final layer is the output layer. The output layer contains a single fixed node. It computes the final output by summing all input signals which can be described as:
The training process of ANFIS follows a hybrid learning mechanism for acquiring an optimal set of rules. It learns by updating antecedent and consequent parameters iteratively by keeping one set constant while updating the other. ANFIS uses Least-Square Error (LSE) methods for optimizing the Consequent Parameters {α, β, r} in the forward pass whereas uses GD to update antecedent Parameters {a, b, c} in the backward pass. Calculating gradient at every step can be very difficult and also comes with the risk of getting trapped in local minima [30]. Moreover, convergence in the GD method is quite slow and heavily depends on the initial values of ANFIS parameters. An evolutionary algorithm such as PSO can provide an alternate solution to these types of problems. Although, there exist other techniques for parameter optimization such as grid search, random search, genetic algorithm, etc. but, PSO appears to be more appropriate choice for this study because of its simplicity, low computational cost as compared to genetic algorithm, quick to converge to optimal solution as compared to grid search and random search and doesn’t require calculation of derivatives like GD. Thus, these interesting features of PSO motivated the investigators to apply it in updating the trainable ANFIS parameters.
2.2. Particle Swarm Optimization (PSO)
PSO is a population-based metaheuristic algorithm proposed by Dr. Eberhart and Dr. Kennedy in the year 1995 [31]. The idea of PSO draws inspiration from the social behavior of bird flocking or fish schooling. The goal of this algorithm is to find an optimal solution (global best) among all possible solutions in a given search space. Every particle is associated with a fitness value calculated by evaluating a fitness function and a speed factor by which a particle moves within the flock. Initially, particles are spread across the search space randomly. At the end of every iteration, a particle updates its knowledge about two important information (i) The best fitness value it has computed so far, known as personal best (PBest) and (ii) The best fitness value discovered among other particles known as the global best (GBest). Based on these two information particles calculate the speed or velocity at which it should move so that it can reach closer to the global solution or GBest. It can be visualized with an example included in Fig. 2.
Particles gradually adjust their position and traveling speed dynamically by learning from own experience as well as of its colleagues as shown in Fig. 2. With the current velocity Vi(t) of the ith particle, it tends to move away from the GBest. However, with PiBest and GBest included in the equation particles are forced to fly closer to the global solution. The way these particles update their velocity and positions can be explained by the equations given below as discussed in [32]. The process is repeated until target value or the maximum number of iterations is attained.
Here, Vi(t) is the velocity with which the ith particle is moving. Pi(t+1) is the updated position of the particle based on its current position Pi(t) and moving velocity Vi(t + 1). PiBest and GBest are personal and GBest values as discussed earlier. The values r1 and r2 (ranges between 0 and 1) are random values regenerated for each velocity update. c1 and c2 are the rate of learning parameter and c1, c2, w are user supplied coefficients.
3. Methodology
3.1. Study Site and Data Used
The study area used in this investigation is Dikhow basin, India. The Dikhow River is one of the important tributaries in the southern bank of the river Brahmaputra. The major area of the basin lies in Nagaland. It originates from the Nuroto Hill area in the Zunheboto district. The river flows towards the north along the border of Tuensang and Mokokchung districts. The river further flows northward and leaves the hill near Naginimora and passes through Sibsagar city of Assam. The Central Water Commission (CWC) gauge station located near to the Brahmaputra main channel is considered as the outlet of the Dikhow River for hydrological modeling. The basin area is 3,292 Sq. km. The length of the river up to the confluence of Brahmaputra is approximately 330 km. The annual rainfall of the Dikhow basin varies between 1,431 mm to 2,597 mm. The maximum rainfall received for this basin is from May to September. Rainfall-runoff readings from May to September from 2006 to 2018 are collected and considered as the input to our predictive model. The location of Dikhow river basin is shown in Fig. 3.
3.2. Selection of Inputs to the Model
Any data-driven model is sensitive to the quality of input data. Therefore, data must be preprocessed before being used in any modeling process. Runoff data gathered at a daily interval is essentially an example of time series data. In time-series data, summary statistics like mean, variance, autocorrelation (ACF), etc. of input data keeps changing over time. Which can provide additional information that can be used in the model building along with existing data. However, in most cases of time series analysis, the dataset needs to be analyzed, transformed and processed to get the desired result.
This present study employed a statistical approach as suggested by Sudheer et al. [33] to identify the suitable input parameters. The approach works on the assumption that variables of importance with respect to different time lags can be identified by analyzing cross correlation, ACF and partial autocorrelation (PACF) between the variables under consideration. Detailed explanation of PACF in runoff estimation can be found in [34]. In this experiment, we have used PACF to analyze our input dataset. Fig. 4 (a) and (c) show that rainfall and runoff in the Dikhow basin are significant up to 4 lags, respectively. Hence, a total of 8 parameters as shown in Eq. (9) are chosen as input to the model.
where, R represents the rainfall and Q represents the runoff.
In transformation, the most commonly used approach is known as sliding window technique. Assuming original time series to be X = {X1, X2, ···, Xn}, applying sliding window will give us Y which includes several Yi’s of the form Y i = {X i, X i + μ, ···, Xi + (m − 1 ) × μ}, for i = 1, 2, ···, n − (m − 1)μ. Here, μ is the lag and m represents the window size. In this experiment μ is set to 1 and m is determined by using PACF technique discussed above.
Ideally, we want our time series estimation model to extract any kind of systematicities present in the time-variant data. However, we also do not want known or obvious systematicities to affect its performance. That is why classical time series analysis techniques convert non-stationary time series data into stationary by identifying and removing trends and seasonal effects. A very common way of doing this is by using the differencing process. It basically finds the difference between two successive values as shown in Eq. (10). Thus, the linear trend available in the data is rectified.
Besides analysis and transformation, certain preprocessing steps are also required. Neural network based models are sensitive to variance in the input data. Data preprocessing steps like normalization can help to reduce the overall processing time and improve network consistency as well. Normalization can be performed as follows:
After performing these basic steps, the input data are then split into 70–30 ratio for training and testing purpose, respectively.
3.3. Performance Evaluation Criteria
There are numerous performance evaluation matrices available in the literature. However, in the absence of any universal evaluation standard researchers often use multiple techniques to reflect upon one or more characteristics of the developed model. In this study, a statistical measure known as coefficient of determination (R2), coefficient of efficiency or Nash-Sutcliffe efficiency (NSE) and the root RMSE are used for performance evaluation purposes. R2 represents the degree of determination among the measured and predicted values. Its value typically ranges between 0 and 1 indicating no and perfect fit between data points and best fit regression line, respectively. The value of NSE ranges from -∞ to 1 and it is often used to evaluate the model’s predictive power. Similarly, the RMSE is the measure of the average magnitude of the error. It represents the square root of the average squared differences between prediction and actual observation. All these indices can be defined as follows:
Where Yi and Ŷi represent the measured and predicted outcome for ith data, respectively. n is the total number of data points considered in the performance evaluation process and Ȳ, Ỹ represents the mean of measured and predicted value, respectively.
3.4. Model Development
This investigation used PSO-ANFIS as the primary forecasting algorithm for rainfall-runoff estimation. As already discussed in section 2.2, ANFIS is a hybridization of two other machine learning algorithms namely ANN and FIS. The performance of ANFIS highly depends on the accuracy in estimating the weight and bias parameters of ANN. Here, we have used a metaheuristic technique known as PSO for estimating model parameters of ANN. The discussions about the model development process are as follows.
3.4.1. ARIMA model
ARIMA model’s performance depends on the selection of three primary components, AR (autoregressive term), I (differencing term) and MA (moving average term). It is commonly represented as ARIMA(p, d, q); where, p denotes the autoregressive term, d is the differencing factor important for data stationarity and q is the moving average window size. The necessary model configuration was done through the analysis of autocorrelation function (ACF) and partial autocorrelation function (PACF) plots generated from runoff data analysis. ACF and PACF provide an initial guess about the different lag factor. As can be seen from Fig. 4 (b) and (c), approximately, first 50 lags on ACF plot and 4 lags in PACF plot shows a significant positive correlation. Therefore, the choice of p = 50, and q = 4 would give an initial choice to begin with. However, the actual values of p, d and q were selected on a trial and error basis. Different values were tried and the best result was achieved using ARIMA(10,1,4).
3.4.2. ANFIS and PSO-ANFIS model
The initial parameter settings of PSO–ANFIS used in this experiment are discussed as follows. The cognitive factor c1 and the social learning factor c2 were both initially set to 2. The number of particles and iterations were set to 100 and 500, respectively. The inertia weight was set to 0.5, the maximum velocity was set to 3. Random numbers r1 and r2 are kept within the range of 0 to1. Most of the PSO configuration was done by trial and error method with values adopted from the work of Eberhart [31].
In the case of ANFIS, the model was created using the discussion presented in section 2.1. Initially, training data are partitioned into clusters to construct the initial ANFIS. Some of the available clustering choices are grid partitioning, subtractive clustering, fuzzy c-mean clustering, etc. In this case, fuzzy c-mean clustering is chosen for creating the initial FIS because of their superior performance as claimed by many researchers [35]. In ANFIS, there are 2 sets of trainable parameters available in the form of antecedent part parameters and consequent part parameters. We have used the GMF in the antecedent part as there is no explicit theory available to substantiate the rationale behind selecting a particular type and number of MF [36]. Therefore, the required number of MFs is determined via trial and error method. In this experiment, the best prediction was acquired using GMF which can be defined by the following equation.
where, is the variance, is the crossover slop and is the center of MF.
In the training process, ANFIS uses a two-step process. A typical ANFIS uses the least squares method and the backpropagation GD method to optimize different trainable parameters. In every iteration, one of the parameters set is updated. In the forward pass, nodes output till the fourth layer are calculated and then least square method is used to update consequent parameters before calculating the final output. Similarly, in the backward pass, the error is back-propagated till first layer where the GD method is used to update the membership function parameters. The final FIS parameters of the ANFIS model gets determined when the stopping criterion of the training process is met.
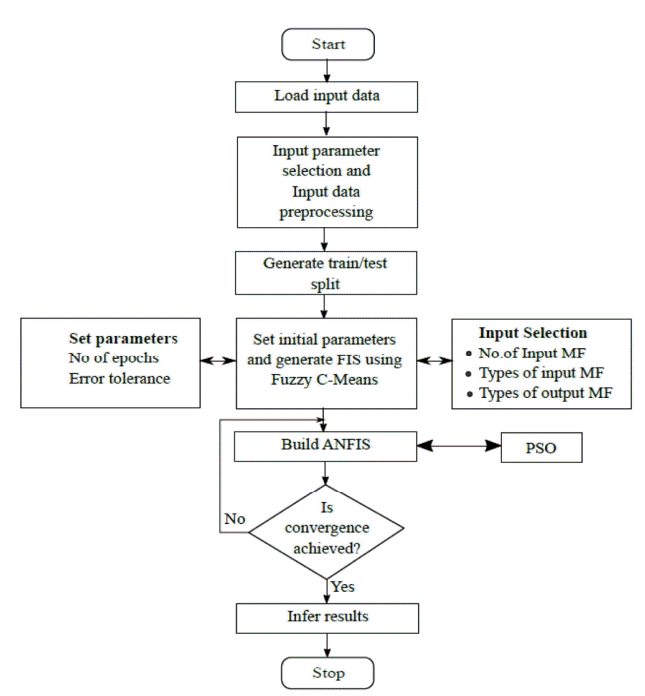
With PSO-ANFIS, the training process is carried out a little differently. Initially, trainable parameters are initialized with random values and then PSO is used to update them. In every iteration, out of two parameters set, one is updated keeping the other constant. Finally, after updating all the parameters again the first set of parameter update is considered and the process goes on. These parameters are usually assembled in a vector form which is updated in every iteration. The updating process is carried out using the steps discussed in section 2.2. The overall working of PSO-ANFIS can be understood using the flowchart given in Fig. 5.
4. Results
In order to model rainfall-runoff relationships, historical time series of rainfall and corresponding runoff values with different time lags were examined in this experiment. For uniformity in model building, the same set of training and validation data were used. For performance evaluation purposes, statistical error measures such as R2, NSE, and RMSE have been used. From Table 1 it can be observed that all three methods have different performances during both the training and testing phases. In the training phase, the PSO-ANFIS model achieved about 0.3% and 0.6% improvement over conventional ANFIS in terms of NSE and RMSE, respectively. Whereas, in comparison to ARIMA, it achieved an overall improvement of 0.89% in terms of NSE and a 1.19% reduction in overall RMSE. A similar trend was found in the testing phase as well. PSO-ANFIS measured an improvement of 2% and 9% in terms of NSE value over conventional ANFIS and ARIMA model, respectively. At the same time, it measured a slight reduction of 0.2% and 1.2% in overall RMSE value over conventional ANFIS and the ARIMA models, respectively. However, total computational time (validation time) as shown in Table 1, suggests that the ARIMA model was superior in computing the result. Proposed PSO-ANFIS model took 1.45 s more than the ARIMA model but took 3.8 s less than ANFIS to produce the result.
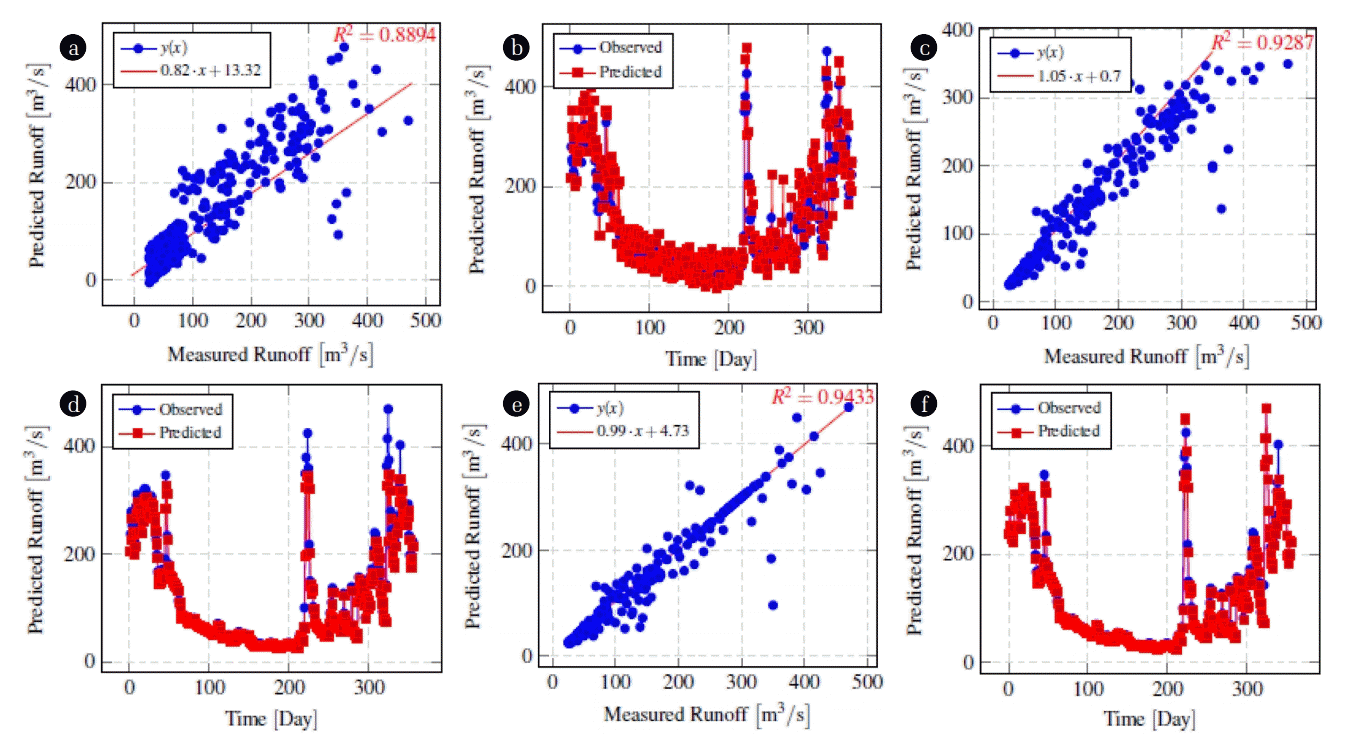
In addition to the NSE and RMSE measure, The PSO-ANFIS registered better R2 value as well. Fig. 6 shows the prediction and correlation graph of all three models. The proposed PSO-ANFIS achieved R2 equal to 0.94 which is better than that of R2 value of 0.92 and 0.88 of ANFIS and ARIMA model, respectively. This shows the presence of a higher correlation between observed and predicted runoff in the PSO-ANFIS model. Moreover, if we observe the observed vs. predicted runoff plot, we can see that PSO-ANFIS is able to predict the high and extreme runoff values more effectively. For instance, the extreme value of 400 m3 and above runoff values is best predicted by the PSO-ANFIS model. Overall, we can say that PSO-ANFIS model outperformed ARIMA and conventional ANFIS in all aspects except the computational time where ARIMA performed the best.
5. Discussions
From the analysis of the result presented in section 4, it is clear that PSO-ANFIS performed better than the conventional ANFIS model. This is because the output of ANFIS is dependent on the performance of ANN which in turn depends on the accuracy in estimation of its weights and biases. In modified ANFIS, swarm intelligence technique like PSO has been used to estimate the parameters of underlying ANN. Since PSO is a metaheuristic-based optimization algorithm it makes very little or no assumptions about the problem being modeled. This implies that PSO does not use the gradient of the problem during convergence. Hence, eliminates the probability of chances of models being trapped into local minima or vanishing gradient like problems. This helps in providing the major advantage of using PSO over GD and as a consequence, improved accuracy and convergence speed could be achieved.
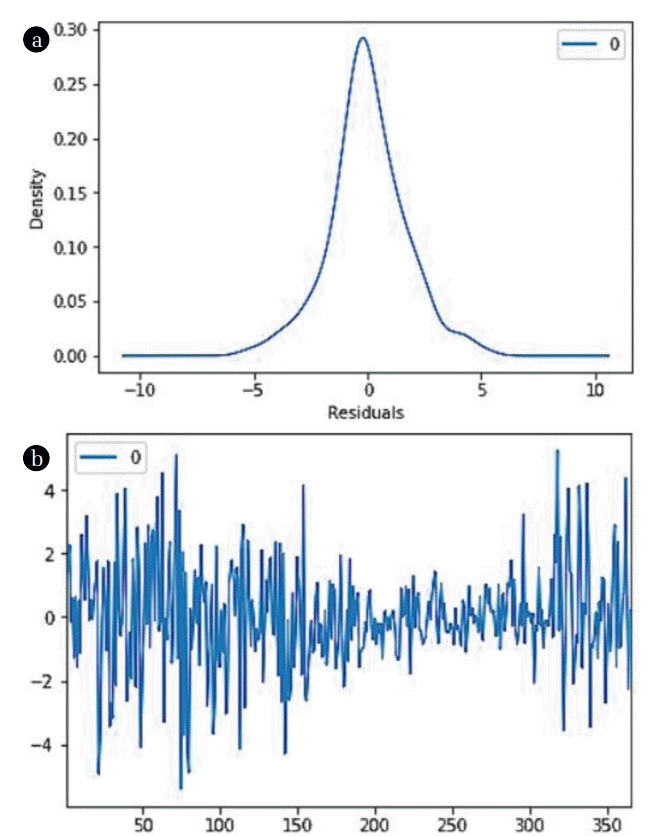
A comparison of proposed PSO-ANFIS with the ARIMA model reveals that the former has been able to predict runoff values more accurately. However, ARIMA performed better with respect to computational time. It is worth mentioning here that, ARIMA is a univariate time series estimation model. This means, ARIMA model in this experiment is built solely using historical runoff data. This is in contrast to ANFIS or PSO-ANFIS models which have the leverage of using one exogenous variable in the form of rainfall data for the model building purpose. Considering this fact, the performance of the ARIMA looks satisfactory to some extent. Fig. 7 shows the residual of forecast error with mean = 0.014 and std = 1.681 which is highly acceptable. Adding extra rainfall attribute in the model equation will certainly help to achieve an even better result. Such a multivariate version of ARIMA models is commonly known as ARIMAX model. Development of such a model can be considered as future scope of this work.
Statistical estimation techniques like ARIMA often suffer from the problem related accuracy. This is due to the fact of a linear representation of a non-linear system [37]. The process also gets affected by the presence of noise and measurement inaccuracies. Therefore, ARIMA often fails to capture the extreme situations satisfactorily. Besides, these techniques also require a high volume of continuous historical data [38]. Fortunately, the performance of machine learning-based approaches like ANFIS or PSO-ANFIS is less dependent on the quality of the input data. As a result, the proposed PSO-ANFIS model performed better than ARIMA which is apparent from the result shown in Table 1. From reading presented in Table 1, it can also be observed that the computational time required by PSO-ANFIS is slightly higher than ARIMA but significantly lower than conventional ANFIS. This indicates the strength of the PSO-ANFIS in forecasting runoff data. The Table also indicates the result in terms of statistical error measures, the performance of PSO-ANFIS is better than the ARIMA and conventional ANFIS techniques.
4. Conclusion
Rainfall-runoff estimation is a very important process in hydrology. It usually provides support for different water resource planning and management activities. Designing a physical model for such phenomena is often a costly affair and requires absolute domain expertise too. Therefore, machine learning techniques are commonly used to discover a hidden relationship. In this study, a popular modeling technique known as ANFIS, augmented with PSO is presented for modeling the rainfall-runoff relationship.
Experimental result as included in Table 1 suggests that modified ANFIS performed better in terms of RMSE compared to ARIMA and conventional ANFIS. The PSO-ANFIS’s prediction results as shown in Fig. 6 also indicate how well it has modeled the hidden nonlinearity. These results are quite satisfactory. Overall, it can be inferred that because of the simplicity of the PSO algorithm (no gradient calculation at every step) the convergence and overall accuracy of PSO-ANFIS has improved. Thus, it can be concluded that ANFIS-PSO provides a viable solution to modeling complex problems such as rainfall-runoff with considerable accuracy.
However, it should be noted that instances like this (rainfall-runoff) are very specific. The variance in the dataset differs from case to case which often leads to contrasting results. There are evidences available where ARIMA outperformed ANFIS and vice versa [39–40]. Therefore, in future we would like to extend our research with other basins data as well as some other problem domain to best support this conclusion.