A micro scale in this research is defined as the space within a near homogenous sub layer of the troposphere [18]. In this case, we consider the surface layer of the troposphere. Therefore, at layer 2 of the PBL (surface layer), the aerosols number density ranges between 140 cm⁻³ and 515 cm⁻³ in clean tropospheric air and polluted urban environments [19–20]. Hence, the aerosol content dynamics mimics the aerosol density distribution solution given by McKibbin [21] in Eq. (19). If ‘a’ in Eq. (18) is analyzed such that the vertical profiling is done with respect to time, then it is not a constant because of its transverse dispersion expressed in Marco et al. [22]. The translation of ‘a’ from a constant to variable is referred to as a particular case where the aerosols transport is within a confined micro-scale system in the Stokes’ regime [23].

Here, Q is the mass of the particle released above the ground from the cement factory, D_L is the longitudinal dispersion coefficient, D_T is the transverse dispersion coefficient, t is the time taken for the aerosol to reside at each layer, V_x is the wind velocity (m/s) t is the time taken. In the mild diffusion region, D_L = D_T because the particles becomes lighter and more energetic [24–25] and reaches its quasistationary level at about 10,000 s [26] before atmospheric blocking takes place [27]. Hence, Eq. (19) may be written as $a=\frac{Q}{4000\mathrm{\pi }{D}_T}$, then

From the refined Eq. (20), the wind velocity is a major function of the aerosol content dynamics (δ). The wind dynamics was harvested via the Davis Weather Station which was mounted about 1.2 km from the research site (cement factory). First, we determined the theoretical expectation of δ (Fig. 1–3) by assuming that the chunk of the mass of the particle released above the ground from the cement factory is about 4–10 kg within 1,000 s. Three cases were considered i.e. when the mass (Q) ejected do not decay (Fig. 3(a)), when the mass (Q) ejected has a logarithmic decay (Fig. 3(b)) and when the mass (Q) ejected has an exponential decay (Fig. 3(c)). The three conditions were adopted from Drewnick et al. [28] aerosol quantification where different atmospheric decay conditions were discussed.

When the mass ejected do not decay or vanish, the PBL experiences massive aerosol loading which increases linearly as shown in Fig. 3(a). This means that life forms are exposed to radiative heating effects which are as a result of either massive absorption or scattering of radiation from the sun by the aerosols. When the mass ejected are decaying exponentially or logarithmically, the aerosols loading in the PBL are reduced by rainfall or wind. However, the tendency of the aerosol loading to concentrate at specified sub-layer of the PBL e.g. surface layer may be enhanced by human activities. This possibility is represented in the term P & S in Eq. (1).

In the three cases illustrated in Fig. 3, the aerosol mass deposition is the most consistent parameter. Hence, the accuracy of the aerosol mass deposition was affirmed in Table 2 i.e. compared to the experimental air pollutants deposition at various sampling points reported by Olaleye et al. [29]. The aerosol content dynamics increases in magnitude in either of the cases mentioned earlier. This shows that the wind speed is the trigger for aerosol advection or deposition. We monitored the readings of both the wind speed and its direction for January (see Fig. 4). Fig. 4 is the wind speeds corresponding to the monthly averages. We harvested the first twenty events of the directional coordinates of the wind in the 1,200 s at various intervals. Recall that the Davis Pro II weather station was positioned at the surface layer of the PBL to see the effect of the wind speed on the aerosol content dynamics. The main characterization for standard divisions for the magnitude of wind speed within different directions over the research region has been reported in [30]. The wind speed in January showed greater tendency to transverse the west-south-west (WSW) or south-west-west (SWW). From Fig. 4, the wind speed at WSW is high and has more consistent trend than other wind directions. Other coordinates i.e. SW or S exhibit inadequate trend. Hence, it supports few abnormalities observed in Table 2. Therefore, the three dimensional semi-plume model determines rather the deposition points and two dimensional semi- plume model determines the wind field dynamics. Therefore, the solution to controlling the flow of air pollutants from any anthropogenic sources is illustrated through the mathematical model in Eq. (4).

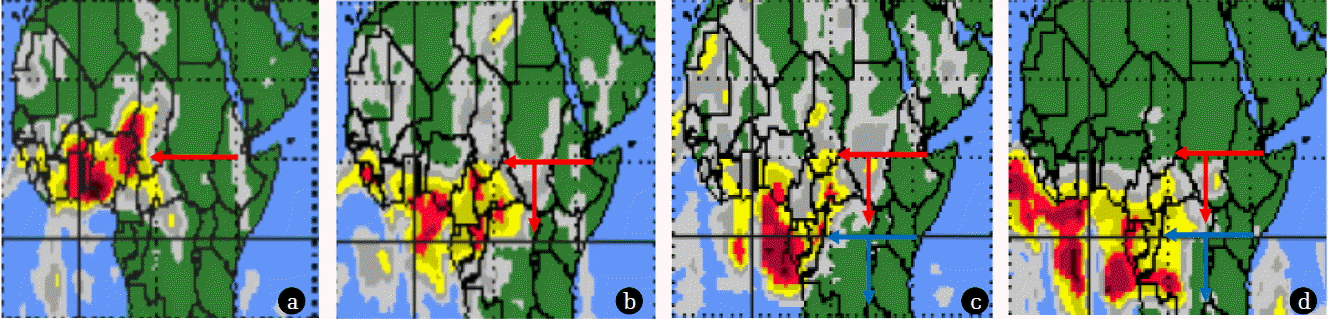
WA is characterized by large aerosols loading as a result of biomass burning during farming season and the natural influence of the harmattan dust via the north-east winds. The aerosol emissions and transport are still affected by large uncertainties. Seeking solutions to the uncertainties via the application of numerical models only have been shown to be inadequate on its own. The greatest of the uncertainties is the influence of climatic change to aerosols transport [31]. In the macro scale analysis, we consider what happens in both the PBL and the free atmosphere because they interchangeably influence each other [5, 32]. The aerosol concentrations used to analyze in Eq. (2) are fixed to zero at the domain boundaries. This step is to allow for the external incoming aerosol amount to be minute at the sources. Since, this assumption is important to simultaneously determine both the vertical and horizontal profile of the atmosphere; there still exists the uncertainty caused by wind recirculation that takes place at the boundary of the PBL and free troposphere. Therefore the Neumann boundary condition is applied to obtain the physics of the aerosols physical tendency during transportation. Mayya et al. [18] adopted the Neumann boundary condition to analyze particles undergoing turbulent diffusion near absorbing surfaces e.g. PBL. Hence we must know the extent of influence the two media, that is, PBL and free tropo sphere has on the aerosols transport. The volume of pollutant dispersed from its various sources across WA is assumed to possess the same characteristics as shown in Fig. 5 i.e. large volume of diffusing pollutants concentrate at about 100 m above its dispersion source. This idea is drawn from the fact that aerosols may be radioactive and nonradioactive [1, 33]. Hence the assumption that particles possess the same characteristics is scientifically viable since the particles are in motion. The maximum range of the diffusing particulates at a maximum speed of 5 m/s is about 100 m. The volume of pollutant at this point is very low (Fig. 5(a)). At macro scale dispersion (Fig. 5(b)), the same characteristics shown in the micro scale transport is experienced. This further affirms that the radioactive or nonradioactive state has no adverse effect on the aerosols transport. The difference between the micro and macro scale is that the maximum speed of the macro scale is less than 4.4 m/s. This low speed enables the pollutants to acquire maximum range of about 15 km. Fig. 6 shows the aerosol transport within four years. The red colour depicts region of very dense aerosol particulates, the yellow colour shows the region of dense aerosol particulates, and grey colour shows region of light dense aerosol particulates. A comparative study with satellite observation in Fig. 6 shows that the type of aerosol in Fig. 6(b) and Fig. 6(d) can be classified by their peculiar transport (y-direction) as made-up of dust, smoke, soot, etc. This result agrees with the peculiar transport of mainly dust [10] or smoke [34] which has been investigated. The implication of this result is that atmospheric aerosol could build-up with time. If the aerosol is of higher lifetime, the aerosols transport has the tendency of shifting farther than its source of dispersion. The TOMS AI observation for January of 2000–2003 of WA (shown in Fig. 6) affirm the shifting tendency of built-up aerosol travelling at low speed. This type of aerosol is known to absorb ultraviolet (UV) rays. UV absorbing aerosol is dependent on the altitude, hence, the higher the aerosol altitude, the greater the fraction of affected molecular radiation. In view of this research, the UV absorbing aerosols might be affected by the northeast monsoon, rapid chemical transformations and aerosol removal processes.

The shift from the red arrow in 2000 southward and its continuous glaring shifts (the blue arrow) in 2001, 2002 and 2003 affirmed the macro scale functionality of the model. Though it will be quick to affirm that the shift was due to the global climate teleconnections (GCT), however, the science at which this aerosols shift towards the coastal belt is quite unique and may not be explained using the aerosols micro-scale transport. GCT includes climatic oscillations and regional climate systems. The climatic oscillation includes El Nino-Southern Oscillation and North Atlantic Oscillation. The North Atlantic Oscillation originates eastward from the southwestern North Atlantic to Portugal and West Africa. Therefore, there exists another explanation with respect to the aerosols transport alongside the gradual annual shift of the aerosol due to GCT. A further analysis on the y-axis transported as viewed by the satellite sensor (Fig. 6) would enable us to understand the physics of the aerosol transport with respect to the changing angular satellite imagery capture.

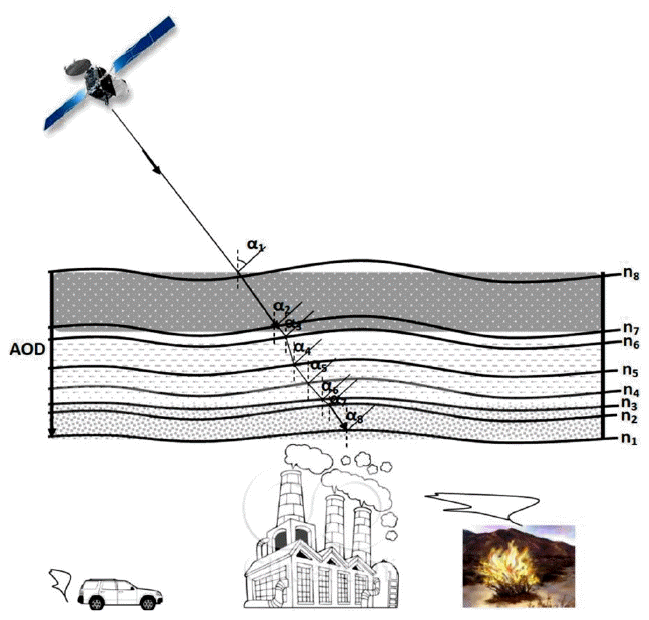
We assume that if the moving aerosol is viewed from the satellite sensor that is relatively moving at the earth’s rotational speed, it will experience multiple refractive indexes which affect the actual measurement of the AOD. In Fig. 7, the satellite sensor has the challenge of evaluating the right refractive index of a moving aerosol. If we adopt the results from literature [25] for the x-direction transport-where the aerosol travels at a speed of 4.4 m/s, then the illustration in Fig. 8 can be easily evaluated.

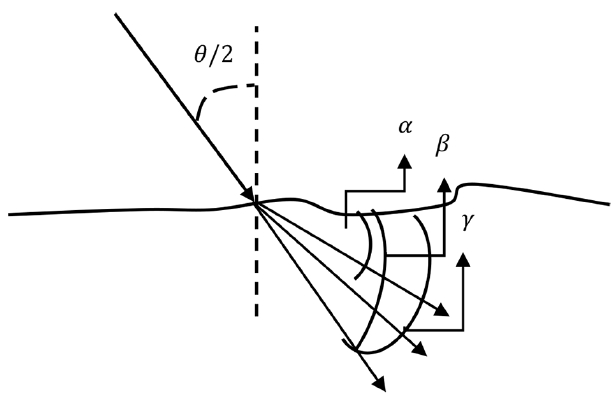
We propose that the number refracting angle depends on the type of aerosols, its speed and the incident angle of the satellite sensor. Let us assume that three refracting angles of the signal are α, β, and γ. Hence from the basic of refractive index

If the trigonometric rule $\left[\text{sin}\mathrm{\theta }=\left(\text{sin}\frac{\mathrm{\theta }}{2}+\text{sin}\frac{\mathrm{\theta }}{2}\right)\text{cos}\frac{\mathrm{\theta }}{2}\right]$ is applied for a full incident angle from the sensor, then

Since the relative air mass of a typical sunphotometer is written as $m=\frac{1}{\text{sin}(\mathrm{\theta })}$, then the concentration of pollutants (C) can be expresses as

If Eq. (9) is substituted into Eq. (8), then

If we compare each terms at the right of Eq. (24) and the right term of Eq. (4), it would be easy to affirm that several dispersion sources determine the complexity of measuring the AOD using the satellite sensor - MISR. The AERONET ground data available on http://aeronet.gsfc.nasa.gov/ for AOD was compared with the satellite data set for Lagos, Nigeria (Fig. 9) for 2011 and 2013. The monthly average AOD data set of both the satellite and ground stations were obtained and plotted as shown in Fig. 9. The statistical analysis shown in Table 3 further affirms our guess on the actual aerosols dispersed from the earth and the migrated aerosols in the tropopause and stratosphere.

The two evidences, that is, analytical and field observation affirms the complex nature of aerosols which depends on the geographical location. The micro scale analysis of the range in y-direction reveals that aerosol distribution over the PBL sub-layers showed disturbances at lower range and higher disturbances at higher range. In Fig. 10(a), the possibility of obtaining strange aerosol distribution especially when they begin to coagulate via inelastic collision was expressed. The perturbative nature as shown in the 3D micro scale analysis further corroborate the wind recirculation effect on aerosols content and rain formation [35]. For example, Fig. 6(a) and Fig. 6(c), that is, in the year 2000 and 2002 showed the intermittent aerosol distribution towards Liberia Sierra Leone, Guinea respectively. The magnitude of the aerosols loading at this differs as the major volume shifts off the coast towards Cape Verde. This phenomenon is numerically illustrated in Fig. 10(b). The wind pattern and the convective activities near the coastal ties may be partly responsible for the aerosols loading extension.

The lifetimes of the aerosols dispersed in the y-direction in 2002 may be below a year (Fig. 6(c)). The macro scale analysis of the aerosol distribution in Fig. 11(a) and Fig. 11(b) showed that the aerosols loading is more dependent on the space than time in the y-direction. This is also affirmed in Fig. 6(a) – Fig. 6(d). We propose that though the possibility that collisions of aerosols may reduce their number concentration, however, it does not affect the conservation of the total particulate mass. This idea can be affirmed by the numerical simulations in Fig. 9(a) and Fig. 9(b).

In literature, atmospheric circulation pattern in the four climatic zones in WA zones is controlled by some salient factors like AEJ, ITCZ, ITD, associated HL, STJ, troughs and cyclonic centers associated with AEW and TEJ. AEJ operates at mid troposphere (600–700 mb) with maximum wind speed above 10 m/s and travels to WA from the East Africa (Andres et al., 2009). ITCZ also contributes to the convective rainfall pattern via the south-north-south displacement. The numerical prediction (Fig. 8(b)) shows that the aerosols loading could travel 15–17 km within an hour under the set condition.