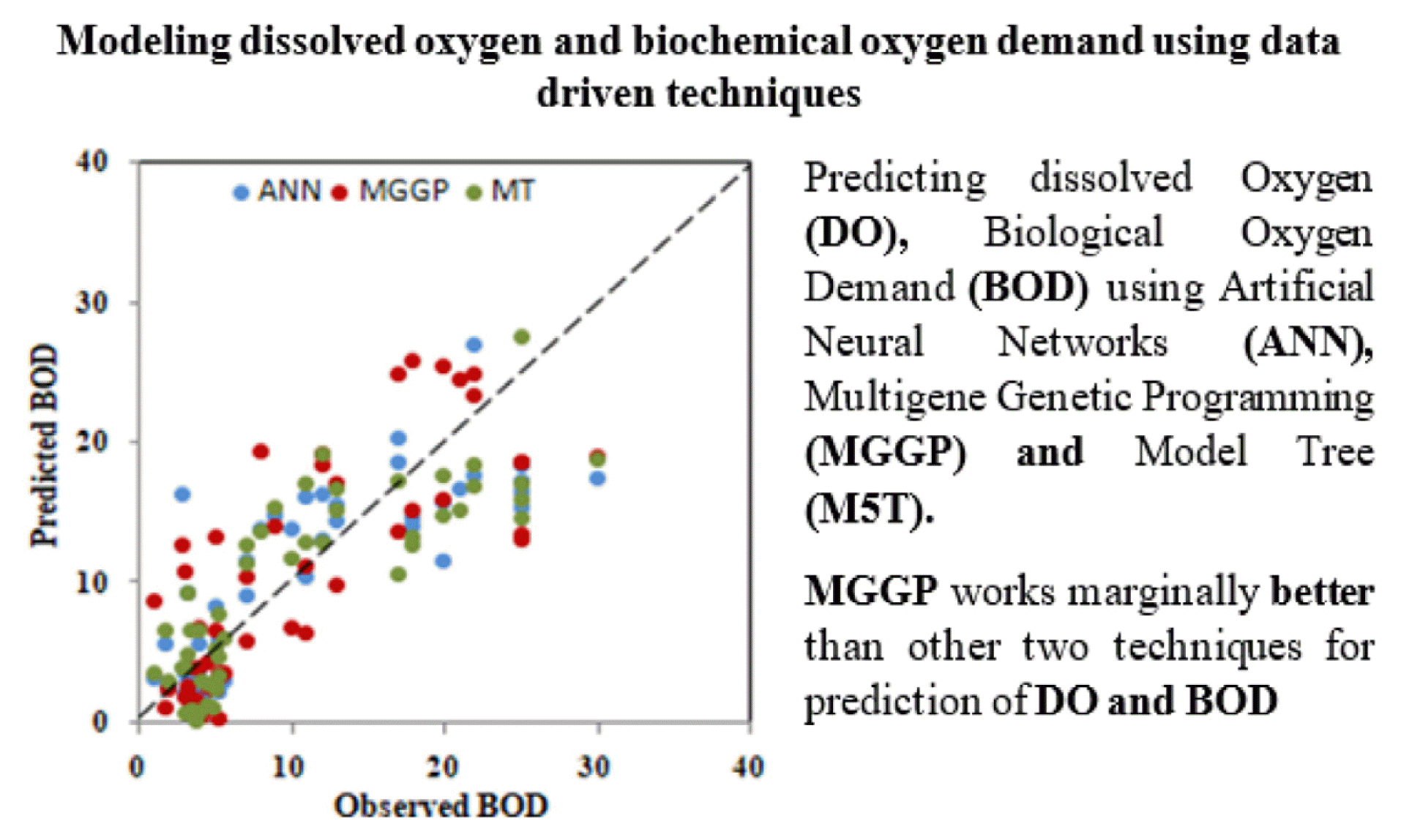
1. Introduction
Water being one of the basic needs of human being, role of river is very important in human life. Quality of water is a major concern in India along with other developing countries as 75–80% of the health issues arise from waterborne diseases [1] and the purity of river is pushed down to its threshold due to mixing of untreated industrial and domestic wastes. The timely monitoring and control of surface water quality parameters has become a major concern due to the above-mentioned issues. Water quality monitoring includes measuring and monitoring of wide variety of physical, chemical, and biological parameters.
One of the important categories of river pollution is organic pollution and drastically affects the ecological health of ecosystems quantity of organic matter present in any river directly influences biochemical oxygen demand (BOD), chemical oxygen demand (COD) as well as dissolved oxygen (DO) content. Biochemical oxygen demand represents the amount of dissolved oxygen utilized by microorganisms to convert the organic matter (biodegradable) to stable inorganic form. COD is considered as the total quantity of oxygen consuming substances in the complete chemical breakdown of organic substances present in river or water. The DO is another key parameter in river water quality analysis as it represents the amount of free dissolved oxygen present in the water body. Considering the organic pollution, DO, BOD as well as COD becomes the main parameters to analyze the quality and pollution status of river. Measurement of COD in laboratory is time consuming and cumbersome as well as presence of various inorganic interfering matters at times, distorts the results [2]. To undertake the BOD determination, traditionally water sample of water source is diluted with aerated water and kept under incubation in the dark at 20°C for 5 days and the DO of the same is determined initially on day 1 and after 5 days. These methods do not consider algal respiration and ammonia oxidation and thus are less accurate [3]. Additionally, the method is too protracted, tedious, and subjected to various measurement errors [4]. To overcome these limitations there is a need to device alternative techniques to estimate COD, BOD, DO and subsequent Management. Some appropriate, reliable, and quick methods for the water quality monitoring with particular reference to DO, BOD and COD is essentially required. Many researchers have attempted in utilizing data driven techniques (DDT) for predictions of BOD and DO [3].
Data driven technique (DDT) is an approach that extracts the relationship between system state variables (input-output) of a specific system by using computational methods that would supersede or replace knowledge driven model based on physical behaviour [5]. Data driven techniques can also be referred as a computational approach with contribution from data mining, knowledge extraction from data base, artificial intelligence, soft computing, machine learning and pattern recognition. The advantage of using data-driven models lies in the computational methodology that helps uncover non-linear and complex relationships between system variables [6]. The basic goal of DDT is to minimize the difference between observed and simulated output. Examples of most commonly used DDT for water quality parameters are Artificial Neural Networks (ANN), Genetic Programming (GP), and Fuzzy Logic (FL).
Out of the three techniques mentioned above the ANNs have been used to predict DO [7–9] and BOD and DO [4, 10] of river water. Basant et al. [3] modelled BOD and DO using linear regression and ANN simultaneously. Results show that ANN performs relatively better than linear regression and shows that ANN was more capable to capture nonlinear relationship existing between variables of complex system. Schmidet al. [11] and Talib et al. [12] employed multi-layer perceptron with back propagation learning to forecast DO and BOD and the results indicated that these models were capable of capturing long-term trend for DO and BOD. Chen et al. [13] developed FFBP-ANN to predict the DO levels of Reservoir Feitsui in China with reasonable accuracy. Sarkar et al. [14] used ANN to predict DO at downstream by using data at the upstream and central part of the river with high accuracy (correlation coefficient = 0.99). Olyaie et al. [15] compared the accuracy of ANN, Linear genetic programming (LGP), radial based function (RBF) and support vector machine (SVM) to predict the DO. The study demonstrated that SVM performs better with 0.99 correlation coefficient followed by 0.96, 0.91 and 0.81 for the best LGP, ANN and RBF respectively. Besides these, many researchers, tried to model DO and BOD using other data driven techniques like Multivariate Adaptive Regression Spline (MARS), Polynomial chaos expansion etc. For example, Heddam and Kisi [16], implemented different technique MARS to simulate DO and compared the accuracy with the least square support vector machine (LSSVM). Studies showed that MARS performed best with the maximum R (0.965) and the minimum RMSE and MAE values of 0.547 and 0.386 mg/L, respectively followed by LSSVM (Least square support vector Machines). All the studies mentioned earlier, it has been observed that ANN is prominently been used to estimate BOD or DO and show a good performance, however the major impediment in its implementation is lack of simple mathematical expression to produce the final output making it less portable [17]. Techniques like Model Tree with M5T algorithm and Multi gene Genetic programming: a variant of Genetic programming is seldom used for the prediction of water quality parameters. The current work thus predicts DO, BOD with observed data and further predicts BOD with predicted DO. The techniques used in the current study are Artificial Neural Network, Model Tree with M5T algorithm and Multigene genetic programming. The novelty of the study lies in the use of M5T and MGGP for modelling DO and BOD. These techniques, though not very new, are sparingly used in civil engineering in general and in pollution studies, perhaps due to the popularity of artificial neural networks (ANN) in the last two decades or so. The major advantage of utilizing M5T and MGGP is that M5T displays its output in the form of series of equations and MGGP displays in the form of a single equation which can be readily used. Further research around Modelling DO using causative parameters can be observed, however modelling BOD using M5T and MGGP can be infrequently seen. Traditional methods also demand time (5 days at least) in predicting DO and BOD and DDT techniques due to their characteristics can compute the predictors faster (in few minutes) [3].
Further in the current study, the accuracy and applicability of both the MGGP and M5T models are compared with the ANN model using statistical error measures of root mean square error (RMSE), mean absolute relative error (MARE), and coefficient of correlation (R), along with visual presentation in form of scatter plots.
The paper is further organized as follow: The techniques used are introduced in the next section followed by information on study area and data. Results and discussions are presented next with concluding remarks at the end.
2. Data Driven Techniques
2.1. Artificial Neural Network
Artificial neural network (ANN) is one of the most flexible mathematical structures developed after considering the working of biological nervous system. It resembles to human brain in two respects: Knowledge to identify the complex nonlinear behavior or pattern acquired by the network through the learning process and use of strength of the interneuron connection known as synaptic weights to store the knowledge. Generally, ANN consists of Input layer, output layer and one or more hidden layers with or without bias at each layer. Each layer consists of one or more nodes or neurons which transfer the information from input to output layer. The neurons in input and output layer are problem dependent (equal to independent and dependent parameters respectively). However, number of hidden layers and neurons in each hidden layer differ from problem to problem and governed by the accuracy requirements. Generally, a three-layered feed forward neural network is found adequate to solve non-linear problems in Civil and Environmental Engineering [18]. The inputs are multiplied by weights and a bias is added to it. This weighted input is then transferred through a transfer function to yield output of the first or input layer. This output then becomes inputs for the next hidden layer and multiplied by layer weights and a bias is added to it. This sum is then transferred through another transfer function (same or different than the first one) to yield output of the first hidden layer. The process is continued till the last or output layer is reached. At the output layer the error is calculated by taking the difference between network outputs i.e., predicted value and the target value. The error is minimized by adjusting the weight and biases by moving in the backward direction using error reduction algorithms till the targeted accuracy in output is achieved. This is called as training a Feed Forward Back Propagation ANN where information is processed in the forward direction and error is distributed in the backward direction. There are other types of ANN as well such as Radial Basis function Neural Network, Generalized Regression Neural Networks, and Recurrent Neural Networks etc. which are out of scope of the present study. The trained weights and biases are then retained and applied on an unseen data for testing purpose. If the model performance in testing is satisfactory which is judged by applying one or more statistical parameters as well as visual inspection, then it is said to be ready for actual operation. The relation of weights with input and output is demonstrated in Fig. S1. Readers can refer to [19–23] for detail working of an ANN.
2.2. M5 Model Tree
Model Tree utilizes divide and conquer approach to provide rules for linear model to reach at leaf node. The linear models are then developed to quantify the contribution of each attribute to the overall predicted value. M5 Model Tree (M5T) is a reconstruction of Quinlan’s M5 algorithm to prompt regression trees of models [25]. M5T combines a standard decision tree with the possibility of linear regression functions at the nodes. For building model trees using the M5T algorithm, an attribute is chosen first on the basis of higher uncertainty or high standard deviation to represent the root node, and one branch is created for each conceivable value; the example set is then divided into subsets, one for each attribute value. Now for each branch, the procedure may be repeated recursively, utilising just the samples that actually reach the branch. If all samples at a node have the same categorization at any moment, the tree’s growth is halted [26–27]. Splitting criteria are used to determine which attribute is picked to be used for a split for a given set of samples. The percentage split determines how much of your data will be retained for training the classifier. The remaining information is used to determine the model’s accuracy during the testing phase. You may make several samples (or folds) from the training dataset using Cross validation Fold. If you choose to build N folds, the model will be run repeatedly N times. And each time, one of the folds is saved for validation while the remaining N-1 folds are used to train the model. The cross-validation result is computed by averaging the results of all folds. The more cross validation folds you employ, the more accurate your model will become. This causes the model to train on randomly chosen data, which increases its robustness [28–29].
Fig. S2 (a) describes the splitting function for the input x1 × x2 variables into various different linear regression function at the leaves namely LM1–LM6 by using M5 algorithm of Model tree. Simplified form of the model equation is y = b0 + b1x1 + b2x2, in which b0, b1, and b2 are linear regression constants and Fig. S2 (b) explains the relation of branches in the form of a tree diagram. For details of MT readers are referred to [28, 30].
2.3. Genetic Programming and Multi Gene Genetic Programming
Genetic programming (GP) is domain independent method that genetically breeds a population of random computer programs to solve the problem. It comes under supervised machine learning which searches its solution in a program space instead of a data space. The solution in the form of programs created by traditional GP is represented as tree structures and expressed using a functional programming language. Genetic Programming (GP) follows the principle of survival of the fittest; the one who is fit is going to survive and involve in evolution of next generation. Initially to generate population, solution is searched blindly in a large space of program by conducting tournament. GP assign a fitness value to each program in a population as a performance task. The two programs that perform the best win the tournament and selected for next evolution. The GP algorithm copies the two winner programs and transposes these into two new programs via genetic operator (crossover or Mutation) i.e., winners now have offspring, and two loser programs are replaced into the population by new child program from the tournament. The creation of new child program continues till a specified number of children in a generation are produced. The best program that appears in a maximum number of any generations is designated as the GP result. Fig. S3 represents the typical GP model and its function, the functions can contain basic mathematical operators (e.g., +, −, X, /), Boolean logic functions (e.g., AND, OR, NOT), trigonometric functions (e.g. sin, cos), or any other user-defined functions.
Multigene genetic programming (MGGP) is a variant of GP. It is designed to create compact mathematical models of targeted response (output) data that are multi gene in nature. In other terms nonlinear input variables are transformed to combined in low order (by restricting gene or tree depth) linear weighted tree. The standard GP representation is based on the evaluation of a single tree (model) expression. In MGGP multigene individuals consist of number of genes, each of which represent as traditional GP tree expression [32]. Firstly, the number of populations and generations are chosen for the MGGP model, which often relies on the complexity of issues and the number of alternative solutions. A huge number of populations and generations are examined in order to develop models with the least amount of uncertainty. Once the population of genes is generated and fitness function values are evaluated, each gene is modified based on the principles of natural evolution with mutations and crossovers, thus producing offspring. The mutation process picks branches, along with sub nodes, and replaces each bunch with a randomly generated sub tree. However, the crossover operation, terminals or branched nodes of parent trees are randomly selected, and the selected points are exchanged. This evolution step is iterated until the termination criterion is met, enhancing the fitness of the models produced. Although maximum number of genes (trees) in an individual, as well as the maximum tree depth, has a direct impact on the size of the search space and the number of solutions examined inside it. The success of the MGGP algorithm often rises when these parameters are increased. Finally, as the output numbers of models are generated, out of that best model is selected on the basis of simplicity as well as greatest fitness value. The user may adjust the simplicity of the model through parameter settings (e.g., maximum tree depth or number of genes). Fig. S4 shows a typical MGGP model generated by 2 traditional GP trees. This model predicts an output variable using input variables x1, x2 and x3. Given model structure contains nonlinear terms (e.g., sin, cos, sqrt.) though linear in the parameters with respect to the coefficients d0, d1 & d2. The function set contain the basic arithmetic operators (+, x, −, √, / etc.) and Boolean logic functions (sin, cos, tanh, etc.). It is relevant to note that the maximum permissible number of genes (Gmax) for a model and the maximum tree depth (Dmax) is specified by the user to have a control over the complexity of the generated model. The evolved models are linear combinations of low order nonlinear transformations of the predictor variables. For details of GP readers are referred [33] and for MGGP readers referred to [17].
3. Study Area
The study area considered in the study is Pune City, which is situated in Maharashtra, India. Pune is the 8th largest city in India, situated on the banks of two rivers, Mula and Mutha. The combined Mula-Mutha river flows through the city of Pune after their confluence at Sangamwadi (Refer Fig. S5). The Mula river travels a distance of about 64 km from its origin in the hilly areas of Pune District, of which 40 km is hilly terrain. It enters Pune city from upstream Balewadi (Latitude 18 34′ 23.17″, Longitude 73 51′ 47.6″) and flows through populated areas of Pune such as Pimple Gaurav and Vishrant Wadi before meeting at downstream Sangamwadi (Latitude 18 32′ 16.6″, Longitude 73 45′ 38.6″) Mula River meets Mutha.
Several villages and small-scale industries like paper mills and sugar mills lie along the banks of the Mula River within the Pune Metropolitan Region, which is responsible for generating waste in the river Mula. The Mula river receives waste from agriculture runoff too (EIA report; PMC 2018). The Mutha River originates in the Western Ghats and flows eastward for about 14 km till it merges with the Mula River in the city of Pune. Many villages and old city areas are along the Mutha River within the Pune Metropolitan region. After merging with the Mula River in Pune, it flows downstream as the Mula-Mutha River to join the Bhima River, a major tributary of the Krishna River flowing southeast. The Mula-Mutha River is the most polluted river as it contains wastewater from various sewage treatment plants as well as common effluent treatment plants (CPCB Report 2019). For the development of BOD and DO models, water quality data set were collected in proportion to the length of the river. The Mula River (30km), the Mutha River (14 km), and the Mula-Mutha River (25km) are all different lengths of river. Moreover, the deviation in the number of data points with respect to the stretch is not more than 10%. The collected data for the Mula-Mutha River was received from Nashik Hydro Works in Maharashtra India from 2003 to 2018 (Water Resources Department Government of Maharashtra, www.mahahp.gov.in).
4. Water Quality Data Set
Water Quality data set required for the current study was collected from Hydro Nashik Maharashtra, India [www.mahahp.gov.in]. River quality parameters are greatly influenced by the anthropogenic activities usually coupled with nonlinear and complex biochemical processes. Biochemical Oxygen Demand (BOD) and Dissolved Oxygen (DO) are influenced by factors like total solids (TS), alkalinity (Alk.), nitrite (No3-N), pH, electrical conductivity (EC), water temperature (Temp.) etc. [10]. To select input parameters for DO and BOD models, it is necessary to understand the relationship of these parameters with DO and BOD.
Salts and other inorganic chemicals dissolve in water and break into tiny electrically charged (Electrical Conductivity (EC)) particles called ions thus increasing the ability of water to conduct electricity while decreasing the potential of oxygen to get dissolved in water [35]. Similarly, an increase in salt (alkalinity) content leading to a high amount of total dissolved solids (TDS) results in lower amount of atmospheric oxygen to get dissolved in the river water stream. As discussed in the earlier section, biochemical oxygen demand is a measure of the biodegradable organic matter present in the water sample expressed in terms of the DO required to oxidize, hence the amount of DO directly influences the BOD content. Nitrite is extremely toxic to aquatic life but it rapidly oxidizes to nitrate (No3-No2), which is responsible for the growth of water hyacinth covering the surface of river making it difficult for the sunlight to reach beneath the water surface decreasing the rate of aeration and in turn the DO demand increases [36], pH is another important water quality parameter which is controlled by inter-related chemical reactions that produce or consume hydrogen ions. Low pH indicates the concentration of hydrogen ions or the increased bacterial activity for organic matter decomposition i.e., low BOD and DO. While pH increases the solubility of phosphorus and nitrates making them more accessible for plant growth and increasing the demand for dissolved oxygen which ultimately increases the BOD content [37, 38]. Water Temperature (Temp.) is a controlling factor for aquatic life: it controls the rate of metabolic activities, reproductive activities and therefore, life cycles. If stream temperature increases, decreases, or fluctuates too widely, metabolic activities fluctuate. The water quality data set required for the current study was collected from Hydro Nashik, Maharashtra, India. River quality parameters are greatly influenced by anthropogenic activities, usually coupled with non-linear and complex biochemical processes. Biochemical oxygen demand and Dissolved Oxygen are influenced by factors like total solids, alkalinity, nitrite, pH, conductivity, water temperature, etc. [10]. To select input parameters for DO and BOD models, it is necessary to understand the relationship of these parameters and DO and BOD.
Salts and other inorganic chemicals dissolve in water and break into tiny electrically charged (EC) particles called ions, thus increasing the ability of water to conduct electricity while decreasing the potential of oxygen to get dissolved in water [35]. Similarly, a rise in salt (alkalinity) content, which results in a large quantity of total dissolved solids, leads in less atmospheric oxygen being absorbed in the river water stream. As discussed in the earlier section, biochemical oxygen demand is a measure of the biodegradable organic matter present in the water sample expressed in terms of the DO required to oxidise it. Hence, the amount of DO directly influences the BOD content. At first nitrite is extremely toxic to aquatic life, but it rapidly oxidises to nitrate (No3-No2), which is responsible for the growth of water hyacinth, covering the surface of a river, making it difficult for the sunlight to reach beneath the water surface, decreasing the rate of aeration and, in turn, the DO demand increases [36]. pH is another important water quality parameter that is controlled by inter-related chemical reactions that produce or consume hydrogen ions. Low pH indicates decomposition of organic matter [37]. Water temperature is a controlling factor for aquatic life: it controls the rate of metabolic and reproductive activities and, therefore, life cycles. If stream temperature increases, decreases, or fluctuates too widely, metabolic activity will fluctuate as well; hence the rate of decomposition by microorganisms will be hampered. [39].
The statistical analysis of the data at the three reaches in Mula, Mutha and Mula-Mutha rivers used in the present study is as shown in Table S1, which includes minimum (min), maximum (max), standard deviation (sd), mean and skewness coefficient. It is clear from Table 1 that the Skewness coefficient (Csx) is quite low for most of the data sets, which is considered appropriate as high skewness value reflects negative impact on performance of ANN [40]. For DO and BOD, the concentrations ranged from 0.0 mg/L, 48 mg/L respectively, which indicates that the samples have lower than the minimum allowable value (CPCB, 2015).
Table S2 and S3 shows the relationship of input parameters with DO and BOD for all three stretches of the Mula-Mutha River. For both the Mutha and Mula rivers, major contributing parameters for DO are EC, TDS, TS, alkalinity, hardness, and pH. However, for the Mula-Mutha River, a different pattern is observed, with pH, TDS, and No3-No2 as the main contributors because No3-N rapidly oxidises to No3-No2, which is responsible for decreasing DO. Similar pattern is observed for BOD too.
Considering the literature, existing records, statistical analysis and correlation behavior, the water quality parameters selected for modelling DO are: pH, Electrical conductivity (EC), Alkalinity (ALK), Total Solids (TS), Total Dissolved Solids (TDS), Nitrite (No3-N) and Temperature (Temp) and parameters for modelling BOD: Dissolved oxygen (DO), pH, Electrical conductivity (EC), Alkalinity (ALK), Total Solids (TS),Total Dissolved Solids (TDS), and Nitrite/Nitrate (No3-N, No3-No2).
To consider suitable input parameters, for model development, correlation between DO, BOD with other independent parameters were investigated. Correlation coefficient is the key indicator of the statistical distribution of given data, and equal to the mean normalized standard deviation of the given data set [4]. High value of correlation (0 to 1) indicates better agreement between the variables. It is reflected from the Table S2 and S3 that variability in samples between Mula and Mutha is not much as compared to combined Mula-Mutha. The variability among the samples might be due to the climatic influences and different pollution trend in the study area. It can be observed from the given Table S2 and S3 that most of the parameters display higher influence of majority of the parameters with DO as well as BOD for Mula and Mutha stations separately except temperature and nitrite and for combined Mula-Mutha station, only pH, Nitrate and dissolved solids reflect higher correlations. Nitrite is generated as an intermediate product during biological oxidation of ammonia to nitrate, it is least stable and usually present in much lower amount than nitrate, and thus the influence of nitrite is seen to be less. Temperature is a parameter which has an inverse influence on DO, but variation in temperature is not very high (Table S1) in the given data set which indicates that some other parameter like suspended, dissolved solids, bacterial decomposition, or any other pollutant, besides temperature is affecting oxygen level adversely, this can be clearly seen in Table S2 and S3 [39].
5. Model Development
In the present work three sets of models have been developed using ANN, MGGP and M5T techniques for 3 stretches of the river, namely, Mula, Mutha and Mula-Mutha flowing through the city of Pune, India. It can be seen from Fig. S5 that Rivers, Mula and Mutha merges to form Mula-Mutha River at Sangamwadi, Pune (Maharashtra). Considering the geographic location and flow of river/s the models are developed as shown in Table S4 with each set numbers and the input parameters considered for each stretch of the Mula, Mutha and combined Mula-Mutha River. The developed models are partitioned in three Sets: In Set 1 and Set 2 DO as well as BOD have been predicted separately using various causative parameters as input parameters. While in Set 3: BOD is predicted using output (DO) from Set1 model as one of the key input parameters along with other input parameters as seen in Table S4. For determination of BOD, pre knowledge of the DO concentration in water is required, thus an attempt is made in Set 3 to consider the predicted DO from Set 1 to predict BOD.
Three layered separate Feed Forward Back-Propagation ANN models were trained to predict the DO and BOD till a low error goal was achieved (mean squared error). All the networks were trained using Levernberg-Marquardt algorithm with ‘log-sigmoid and ‘purelin’ transfer function in the first and second layer, respectively. The data was normalized between 0–1. The model architecture consists of a layer with 6 neurons or nodes as input, a hidden layer with varying range (1 to 32) of neurons as shown in Table 1 and an output layer with a single neuron. The numbers of hidden neurons were fixed by trial-and-error method since selection of an appropriate number of nodes in the hidden layer is very important aspect as a larger number of these may result in over fitting while a smaller number of nodes may not capture the information adequately [41]. For Mula and Mutha stretch optimum hidden neurons are 10 and 11 respectively, however for Mula-Mutha stretch minimum mean square error (MSE) was achieved with 32 neurons. All Models were trained till low error goal was achieved and their weights and biases were retained for testing the remaining data sets. The ANN was trained in the MATLAB 9.1 2016 using NN toolbox [42].
MGGP models have been developed using MATLAB 2016 environment with GPTIPS as source code [32, 42]. The root mean square error (RMSE) function was employed for model calibration. To get the optimum MGGP model various mathematical functions and arithmetic operators have been used. Population and generation reflect the program size and levels of algorithm that is used before the run terminates. The number of population and generation often depends on the complexity of the problem. However, most of the settings to get optimum model were based on experience with the predictive modeling of other data sets of similar size. Maximum number of gene and tree depth directly influences the search space and the number of solutions explored within the search space [17]. The best performing MGGP models have been chosen on the basis of simplicity of models i.e., less complexity and the best fitness value for both calibration as well as testing data set [33]. Complexity of model can also be judged by Pareto chart which represent the entire model generated in terms of complexity as well as accuracy evolved. It can be controlled by defining the values for maximum tree depth and number of gene or tree. MGGP algorithm was run several times by different combination of population and generation till satisfactory result for optimal model was achieved. Population of 500 with 50 generations shows best results as compared to other combinations for Set 1 Mula River. A similar methodology was adopted for Mutha and Mula-Mutha for all three sets. Table S5 gives the details of all the parameter used to Model DO and BOD for a particular stretch.
M5 algorithm for MT was implemented using WEKA 3.9 [43]. To compare the performance of the developed models using the three techniques, the data division for training, validation and testing was kept same as 70% for training, 15% for validation and 15% for testing. The performance of the models developed by using ANN, M5T and MGGP has been assessed for unseen data i.e., data in testing by 3 statistical measures; Root mean squared error (RMSE), Mean absolute relative error (MARE) and Coefficient of correlation (R). To identify the best model MARE and RMSE value should be low as much possible and R should be close to 1 [15].
The form of output of the developed models is important for its practical implementation. ANN displays the model in the form of trained weights and biases, MGGP is the form of a single equation and M5T in the form of series of linear equations. MGGP technique is characterized by the property in which the parameters displaying significantly less, or no influence are extracted away from the final equation. This form of outputs can facilitate the use of these techniques for DO and BOD prediction on site and increases the confidence in the same.
6. Results and Discussion
Results obtained from all three approaches ANN, MGGP and M5T for all models in the three sets for the rivers Mutha, Mula and Mula-Mutha with an aim to predict DO, BOD (With observed DO as one of the input parameters) and BOD (with modelled DO as one of the distinguishing input parameters) are presented in Table 2. It is evident from the results that ANN and MGGP show reasonable results for all the three sets and the models developed using ANN outperforms the M5T and MGGP models. Performance of individual sets is discussed below separately in detail.
6.1. DO Models
Working of ANN model depends on how well the developed/constructed model is trained and the synaptic weight and biases are adapted to provide a meaningful output. ANN Model 1-1 has been developed with an architecture of 6:10:1, with 6 inputs: pH, EC, Alk., TS, TDS, No3-No2 and 1 output: DO and single hidden layer with 10 hidden neurons was trained for the lowest MSE was achieved. ANN model 1-1 exhibited a reasonable performance with the correlation between observed DO and Predicted DO as = 0.89 and with lower RMSE of 0.61 mg/L (Table 2). Lower RMSE depicts the lesser spread of the residual error (between observed and predicted values) i.e., the standard deviation of the residuals and can contribute towards a better performing model with ANN. ANN model 1-2 i.e., for Mula river resulted into a good performing model with R=0.91, however with a higher RMSE of 0.98 as compared to ANN model 1-1. Higher RMSE of 1.52 can be seen for model 1-3 for Mula and Mutha river. The larger RMSE is due to the larger deviation in data which indicates larger spread of data values as compared to values for Mutha and Mula individually. Being sensitive towards higher values, MARE value is also large i.e., 1.52 in Model 1-3. Output ANN in the form of weights and biases can be further analyzed.
MGGP being the next technique utilized, displays the output in the form of a single equation-based model automatically evolves a mathematical expression in a symbolic form, which can be analyzed further to find which variables affect the final prediction and in what trend, and this is the unique aspect of the technique [25]. MGGP develops expressional trees as seen in Fig. S6 for model MGGP 1-2.
The trees are combined using different weights of genes. Table 3 summarizes the equations developed from the trees (genes) and the weights of each gene. The final solution is given by a linear sum of the outputs and a bias value, the weights of which are shown in Table 3 and displayed in Eq. 1. Using the least squares method, the weight related to each tree is determined by minimizing the goodness of fit error between the model and the training set [45].
It can be seen from the above equation that weighing coefficient for electrical conductivity and total solids are higher than other parameters. This shows that these parameters are highly influential in prediction of DO. This finding is in tune with the fundamental knowledge of water quality under environmental studies [46]. Thus, it can be said the data driven technique of MGGP has reasonably understood the underlying phenomenon of DO and the relation of the input parameters with the output. The following can also be seen from the input frequency chart as shown in Fig. 1 below for Mutha river i.e., model 1-1. To provide the identification of input variables that are significant to the output, graphical input frequency analysis of single model or of a user-specified fraction of the population is used [45].
A similar trend can be seen in the frequency analysis chart (not included here) for Model MGGP 1-3 i.e., for Mula-Mutha river. The chart in Fig. 1 depicts the higher contribution of EC followed by alkalinity, No3-No2, total solids and other parameters. This finding is true according to the fundamental knowledge of the DO as stated in section 4 [46]. The equations of each of the genes for model 1-2 are shown in Fig. S7.
From all the models in Set 1 developed using MGGP, model 1-1 and 1-3 i.e., for Mutha river and combined Mula-Mutha river shows higher performance in terms of lowest RMSE. A higher RMSE is seen for model 1-2.
Further MGGP technique evolves multiple model choices to the designer. Any best single model can be selected based on the application requirement with the help of Pareto chart. Pareto chart as seen in Fig. S8 for MGGP Model 1-3 represented the population of the total evolved models in terms of their complexity i.e., number of nodes as well as their accuracy (fitness). The generated models that perform comparatively well and have fewer nodes or less complexity than the best-generated model in the population can be identified in this chart. The best model (high accuracy and less complex) is highlighted with the Red dot/circle. The Pareto (Green dots) represents a model that is not strongly dominated by other models in terms of fitness and complexity, while Non-Pareto (Blue dots) represents dominated models [17,25]. From the Pareto front (Figs. S8), user can decide whether the incremental gain in performance is worth with associated model complexity [25].
It can be seen that in Set 1-1 and 1-3, all the parameters are considered in the equation also depicting their importance and respective contribution as MGGP has a unique characteristic in which the parameter that contribute significantly to prediction are considered while other is removed (as seen in Fig. analysis chart) in predicting the DO [48]. Hence both models 1-1 and 1-3 shown a higher performance and good correlation of all parameters with DO and thus has been considered in the study. Mula river i.e Model 1-2 display a lower performance with a higher RMSE of 1.43 and MARE: 0.06. For Model 1-2 Alkanlinity and pH parameters are not considered in the Eq. 1–2 this is might be the reason for lower performance as alkalinity shows good correlation with DO.
The next technique in discussion is M5T, which works with the underlying phenomenon of Divide and conquer. Fig. S9 shows a typical Model Tree developed by using M5 algorithm for M5T Model MT 1-1 with the linear regression equations developed.
Linear Equation developed for M5T Model 1-1
The above tree shows linear models (LM 1-3) at different leaf nodes. The first number in the bracket shows the corresponding samples in the sorted subset of node and the second number is the root mean square error (RMSE) of the corresponding linear model divided by the standard deviation of the sample’s subset expressed in percentage [25].
Linear equations developed (Eq. 2–4) for M5T Model 1-1 using M5 algorithm show negative coefficient for alkalinity, total dissolved solids and electrical conductivity indicating increase in any of these impurities in river decreases the DO content, which is in line with the theoretical understanding of influence of these parameters on DO [46, 47]. Thus, it can be seen that M5T learns the underlying phenomenon reasonably well. The series of equations developed in MT makes is user friendly.
M5T models developed in Set 1 display a lower performance as compared to the model performances seen in models developed using ANN and MGGP. With higher RMSE and lower R in models M5T 1-1 and 1-3, they show a lower performance. However, M5T 1-2 shows a good performance of R = 0.82 as compared to M5T models for Mutha and Mula-Mutha.
Visual representation of model performances in form of scatter plots for predicting DO using ANN, MGGP and M5T for Model 1-1 (Mutha), Model 1-2 (Mula) and Model 1-3 (Mula-Mutha) is shown in Fig. 2, S10, and S11 below. The scatter plots show a balanced scatter for Model 1-2 rather than Models 1-1 and 1-3. It is evident from the Fig. 2, S10, and S11 that ANN Model 1-2 is able to predict high DO values but display a low performance in prediction of lower low DO values. As far as lower value of DO is concerned MGGP Model 1-2, predicts them better compared to ANN. The M5T Model 1-2 results are slightly less than both ANN and MGGP. It can be observed from the Table 2 that all the three models for 1-2 showing ‘R’ is within 0.82–0.91 range but ANN Model 1-2, has minimum RMSE (0.98).
Mula-Mutha is one of the polluted rivers as it receives lots of waste from various sewage treatment plants as well as commom effluent treatmnet plant, hence the data received from this river reflects a variaton in terms of infleuncing parameter. Table S2 shows, Electrical conductivity, alkalinity and total solids having strong correlation (−0.90, −0.83, −0.84, −0.87, −0.83, −0.81) with DO respectively for Mula and Multha river. While the same parametrs Electrical conductivity, alkalinity and total solids showed the least correalion (0.016, −0.266, 0.128) with DO for Mula-Mutha river. It can be observed from the scatter plot shown in Fig. S10 that MGGP Model 1-3 and ANN Model 1-3, are in agreement with the measured values compared to M5T model. Moreover, the RMSE values for MGGP Model 1-3, are lower (0.08) as compared to ANN Model 1-3 and M5T Model 1-3. Perhaps MGGP approach of rejecting the input parameter that do not participate effectively in the model, making it possible to select correct parameters which is reflecting in better fitness measures.
6.2. BOD Model Using Observed DO along with Other Input Parameters
Set 2 models were designed to predict BOD using observed DO values as input parameter along with other parameters (pH, EC, Alk., TS, TDS, No-N3) as seen in Table S4. The results of these models are then be compared with models of set 3 where in BOD was predicted using modelled DO. This would throw a light on efficacy of the models by virtue of the comparison between the BOD models developed with modelled DO and observed DO.
ANN builds an approximate function that matches a list of inputs to the desired outputs. In the process, it adjusts the weights and biases to reach an expected goal, hence makes ANN flexible approach and can contribute towards better performance [29]. In set 2, model developed using ANN (ANN 2-1) i.e., for Mutha river displays a good performance with R= 0.91 and lower RMSE of 0.12. Model 2-3 (i.e., for Mula-Mutha river) shows a lower performance of R= 0.89. Apart from ANN being one of the good techniques in good mapping of input and output parameters, the statistical parameters of output i.e., BOD also plays a major role. The standard deviation of BOD values in model 2-2 (6.8) is less as compared to that in model 1–1(9.5) and 1–3 (9.53), which indicates a lesser spread of values and thus contributing towards better performance in terms of R (0.92).
MGGP approach displays the output in form of a standalone equation. The equation developed for Model 2-1 (i.e., for Mutha river) is shown in Eq. 5.
Eq. 5 displays higher coefficient towards DO, Alkalinity content and nitrates. Fig. S12 for MGGP Model 2-1 confirms the same by displaying nitrate as an influential parameter with dissolved oxygen being the most influential parameter followed by alkalinity while total dissolved solids as least influential parameter for BOD prediction. DO display its higher influence for BOD because it is the basic requirement for reduction of BOD by oxidation of organic matter. Similarly increase in alkalinity content leads to increase total dissolve solids, which directly increases the organic matter content i.e., BOD [35]. While Nitrates are essential nutrients for plants which can cause plants and algae to grow rapidly in any river, and leads to high BOD levels and depletion of oxygen [49].
The equation developed for Mula river, i.e., model 2-2 is given in Eq. 6 below. The equation displays contribution of DO, EC, TS, pH and No3-N.
Of all the MGGP models developed to predict BOD for Mutha, Mula and Mula-Mutha river, the performance of model for Mutha river is good as compared to other two rivers in terms of higher R and lower RMSE (as seen in Table 2).
In M5T, the input variable that maximizes the targeted error reduction is selected to split the data at that node and the remaining is not considered in the developed equation [29]. The series of equations (2 equations) developed for Model 2-1 using Model Tree is as shown in Eq. 7 and 8 below.
Linear Equation developed for M5T model 2-1
It is quite acceptable from the above equations developed by model tree that DO shows negative coefficients indicating its indirect relation with BOD, followed by positive coefficient to alkalinity indicating its direct relation and for nitrate as a parameter. Performance of M5T model 2-3 in terms of R shows similar value as ANN model 2-3 (0.89, 0.88), though RMSE is slightly at higher side (1.97). Models MT 2-1 show slight lower performance as compared to 2-3. MT 2-2 however shows a good performance for Mula river.
It is evident from the Table 2 that ANN and MGGP both perform reasonably well in terms of low RMSE and high ‘R’ for set 2 models. On the other hand, M5T shows a high correlation (R= 0.85) but RMSE is on a higher side (≥2.12) too.ANN has a flexible approach while in M5T the input variables that maximizes the targeted error reduction is selected to split the data at that node and the remaining are not considered in the developed equation [29]. This can reduce the performance of M5T as compared to ANN.
Visual representation of the results in the form of scatter plots is shown in Fig. S13, 3, S14 for set 2 models developed using ANN, MGGP and M5T. The scatter plots also confirm the above findings and displayed better results of ANN and MGGP in terms of high R (0.91, 0.96) and low RMSE values (0.12, 0.46) respectively, while M5T shows R 0.85 and RMSE 2.12 at higher side. Scatter plot in Fig. 4, displayed a better agreement between the predicted and measured values by ANN. Moreover, high BOD values are also predicted well. Considering the RMSE both ANN 2-2 and MGGP 2-2 showed low values (0.738, 0.98) respectively. Table 2 and Fig. S12, reflects that MGGP is performing better in terms of high R (0.96) and low RMSE (0.49).
6.3. BOD Model Using Modelled DO
Models in Set 3 consist of BOD models by using output of Set-1 model i.e., DO to get insight of how well predicted DO values as well as other influencing parameters able to model BOD. As discussed in earlier section, calculation of DO in laboratory is tedious works and the calculated results are subjected to complicated factors like, absence of resulting oxygen demand from algal respiration leading to measurement error [4]. Thus, the basic aim behind the use of modelled DO is to achieve accuracy and save time. On similar lines of Set 1 DO model, set 2 and Set 3 models for BOD were calibrated and tested and the one with having minimum RMSE or high R were selected.
It may be emphasized from the Table 2 that all the results for BOD prediction in Set 3 depend on accuracy of DO prediction models in Set 1. In set 1 models developed using ANN, Model 1-1 (i.e., for Mutha river) outperforms ANN model 1-2 (i.e., for Mula river) and ANN model 1-3 (i.e., Mula-Mutha river) in terms of R. However, the lower RMSE in model 3-2 and 3-3 (RMSE= 1.84 and 1.85 respectively) is promising. A similar trend can also be seen in MARE. The performances of these models show a decreasing trend as compared to models developed with observed DO (i.e., in set 2).
Models developed using MGGP for Set 3 show similar performances of model 3-1 and 3-2; however, a high RMSE can be seen in model 3-2. The increase in RMSE is due to higher prediction of BOD for few values, thus increasing the standard deviation. However similar to the trend of results seen in ANN models for set 3, performance of MGGP 3-1 model in terms of R is better as compared to other two models (as seen in Table 2). The frequency analysis chart using MGGP for 3-1 (i.e., for Mutha river) is shown in Fig. S15 below emphasis the highest contribution of TS and NO3-N and DO follow by other parameters. DO has a high influence in BOD prediction which was also observed in set 2 and can be seen in all the models in set 3 as well. The set of equations developed for Mutha river i.e., for 3-1 using MGGP is shown in Table S6.
The equation also shows higher coefficients towards Total solids and No3-N and DO. According to the fundamentals, this finding is also correct, since total solids reveal the existence of organic matter, which directly contributes to the increase in BOD, while the presence of nitrite demonstrates the breakdown of organic matter [46, 47].
Model Tree technique for Set 3 models for Mutha, Mula and Mula-Mutha river show a satisfactory performance with a good performance of R=0.81 for model 3-1 but with a RMSE of 1.54. However, model 3-2 and 3-3 shows a higher RMSE (3.93 and 3.5 respectively). Fig. 4 shows the Classifier Tree for M5T model 3-1, and the linear equations (9–11) given by M5T for model 3-1 confirm that model tree has not considered the most important attribute DO for the formation of model, which can be attributed to the splitting criteria of M5T which includes parameters which contributes to minimizing the standard deviation to develop a tree.
Linear Equations developed for M5T model 3-1
Scatter plots shown in Fig. S16, S17, 5 displays under and over predictions and this also confirms the lower performance of all the models in Set 3 as compared to models in Set 2. However, in spite of under or over prediction/s, the scatter plot is comparatively balanced. It can be seen from the scatter plots (Fig. S16) that ANN and MGGP outperform M5T. Fig. S15 displayed relatively higher contribution of Dissolved oxygen, Total solids and Nitrite ions towards BOD prediction in MGGP 3-1 which is in tune with the domain knowledge [46]. It also signifies that the underlying phenomenon is been captured well by MGGP.
Performance of model 3-2 (i.e., for Mula river); shows that both ANN and MGGP displayed satisfactory performance in terms of R (0.80), however M5T model 3-1 yielded the lowest RMSE (1.53). RMSE describe the difference between the models in the units of the variable. The degree to which RMSE exceeds is an indicator of the extent to which outliers exist in the data. It is also observed that few values were over predicted that is acceptable in case of BOD, because high BOD values show organic pollution in any river and demands for treatment.
Fig. 5, and Table 2 reflects better performance of models developed using MGGP and ANN for model 3-3 (i.e., Mula-Mutha river) with correlation coefficient R as 0.8 while MGGP reflecting lowest RMSE 0.98 as compared to ANN and M5T.
As discussed earlier that BOD prediction using computed DO is totally dependent on how well DO is predicted. For Set 1-3 and Set 3-3 both MGGP models are working better as compared to ANN and M5T models, though marginally. Furthermore, during performance assessment of any model for its applicability in predicting BOD or DO, it is very important to know the distribution of prediction error with average prediction error which is evaluated by using Mean absolute relative error (MARE). On the basis of MARE and RMSE index analysis MGGP (0.02, 0.98) is showing better result as compared to ANN (0.21, 1.83) and M5T (0.32, 3.5) for model 3-3.
7. Conclusion
In the present study, an attempt was made to develop a model using ANN, MGGP and M5T for the prediction of two important water quality parameters, namely DO and BOD for three stretches of river, Mutha, Mula, and Mula-Mutha. It can be concluded that all the models have been performed reasonably well, except the model for Mula-Mutha stretch. Models developed by ANN for Set-1 outperformed MGGP and M5T with high R and lower RMSE values owing to its model free nature and capability to map nonlinear input-output. The MGGP model for Set-2 displays better performance for BOD by providing R value more than 0.90 for all the stretches of river as compared to ANN, though marginally. The result of all three set of model seems to be influenced by variability in the data. However, it is to be noted that MGGP worked better than the M5T models in terms of RMSE and R value. Model prepared for BOD using modelled DO for all three stretches totally depends on how well DO is predicted previously and it provides more confidence to the users for the development of model. This study reflects that Data Driven Techniques, like, ANN, MGGP and M5T learn from the data provided in training and try to grasp influencing parameters which are in tune with fundamental knowledge of water quality under Environmental Engineering. Research also shows that all models were unable to maintain their accuracy for low DO values, however, significant improvement is observed for the MGGP for low DO prediction. Thus, further work shall focus on prediction of accuracy for lower DO values. Furthermore, it is also recommended to develop the models by merging the data of all three stretches into one as it would provide more data for training which may improve the overall accuracy.
PDF Links
PubReader
Full text via DOI
Download Citation 
Supplement
Print 
