AbstractAnaerobic digestion (AD) is a biological treatment susceptible to temperature variations. The Arrhenius model and the Van’t Hoff-Arrhenius relationship analyze the temperature effect in AD first-order kinetic constant (k). Kinetic data is relevant for estimating the hydraulic retention time (HRT) in continuous reactors. This research aimed to evaluate the behavior of kinetic constants concerning temperature using the Arrhenius model and Van’t Hoff-Arrhenius relationship and analyze the influence of kinetic constants as estimators of the HRT. The evaluation of the temperature effect in AD analyzed k fit to the Arrhenius model and Van’t Hoff-Arrhenius relationship. The research used data of AD methane yield (B0) kinetics from the literature, corresponding to macroalgae (MA) (25, 35, 45°C), swine manure (SM) (25, 30, 35°C), and co-digestion of chicken manure with sawdust and miscanthus (CM) (35, 40, 42°C). The Arrhenius model and Van’t Hoff-Arrhenius relationship fitted the data with reduced temperature intervals (ΔT = 5°C). The HRT analysis used a mass balance model considering 80% of the maximum B0 compared with the technical digestion time at 80 (T80) and 90% (T90) of the maximum B0. The results indicate that the HRT calculation is sensitive for k below 0.13 d−1.
1. IntroductionThe increase in organic waste products derived from anthropic activities [1], and the lack of management, treatment and disposal systems [2–5] are problems in various countries, mainly developing countries. Alternatives for the treatment of organic fractions include the recovery of nutrients (nitrogen, volatile fatty acids) and the production of non-fossil fuels (biogas and hydrogen) [6, 7]. The implementation of these technologies could have positive economic impacts and improve waste management [8].
Anaerobic digestion (AD) is a technology used for the biological treatment of organic waste [9] with energy production [10]. The AD is a process of microbiological degradation of particulate organic matter (proteins, carbohydrates, and lipids) in an oxygen-free environment [11]. The product of interest is a gaseous mixture mainly rich in methane (CH4) and carbon dioxide (CO2) [12], with the potential to reduce CO2 equivalent emissions and save on the purchase of fossil fuels [13]. AD used as treatment for wastewater produces sludge with high contents of organic matter (45–85%), nitrogen (95–790 mg L−1), phosphorus (13–28 g kg−1), and potassium (1.5–8.2 g kg−1), with potential uses in the irrigation of crops such as corn [14]. Likewise, the treatment of solid waste generates a digestate with a high content of nitrogen (20–40 mg g−1), phosphorus (9.5–25 mg g−1), and potassium (1.1–2.3 mg g−1) [15] with agricultural applications [16].
AD is a complex 4-stages process: hydrolysis, acidogenesis, acetogenesis, and methanogenesis [11], where hydrolysis is the limiting stage of the process [17]. The biochemical methane potential (BMP) assay is a method for evaluating degradation under anaerobic conditions of organic substrates that quantify the volume of methane produced in laboratory-scale batch reactors [18] with applications such as the estimation of methane production rates and organic matter consumption, as well as the evaluation and design of anaerobic treatment processes [17, 19].
Various models evaluate methane production over time for the BMP assay; however, only the first-order model (1) represents the process’s kinetics that coincides with the hydrolysis kinetics [20]. One of the advantages of the first-order model is estimating the time for the production of 80 to 90% of the maximum of methane [21, 22], and the evaluation of the hydraulic retention time (HRT) [23], which has applications in continuous AD reactor design [24, 25]. However, the first-order kinetic model application has limitations because it does not include parameters for direct evaluation of the temperature variation in the process.
The temperature is a factor that affects anaerobic consortia cell metabolism [26, 27], which influences the kinetic behavior of the process, inoculum acclimatization, methane yield, and stability of the process [26, 28–30]. Lettinga et al. [31] identified three thermal regimes: psychrophilic (15–18°C), mesophilic (30–40°C), and thermophilic (60–65°C) for AD. The thermophilic regime positively influences the extracellular enzymatic activity promoting higher hydrolysis rates than in mesophilic temperatures [26], although the thermophilic regime is susceptible to variations of temperature [32]. The literature presents evidence on the influence of temperature on AD, mainly directed towards optimizing operating temperature and strengthening anaerobic consortia [26]. However, there are conflicting results and conclusions due to results that only evaluate methane production and not the behavior of the anaerobic consortia, in addition to not considering the classic model of the three peaks for the analysis of thermal regimes [26]. Some experiences maximized methane production in the mesophilic regime and suggested optimal temperatures of 34.52 [33] and 35.36°C [34] with diverse organic substrates. Although the trends in methane productions are similar to the model of the three peaks and establish that the optimal operating interval is between 35 and 37°C [34], these investigations did not evaluate the effect on the kinetic constant of methane production by first-order models. Likewise, the literature proposes the comparison of the mesophilic and thermophilic regimes by associating them with the recurring operating temperatures in the industry, 35 and 55°C [35], respectively. Although these practices can generate a positive result, they consider that the evaluated temperatures correspond to the optimal ones for each substrate and inoculum.
The literature [20, 26, 36, 37] presents alternatives to evaluate the effect of temperature on AD, among which mathematical modeling relates the kinetic behavior of batch reactors and the operating temperatures. The Arrhenius model and the Van’t Hoff-Arrhenius relationship are approaches to the three-peaks model based on chemical kinetics and represent an alternative for optimizing the AD temperature. The Arrhenius model (2) analyzes the temperature effect in the kinetics of the AD process. Arrhenius model describes an increasing trend up to a maximum point from which it declines rapidly [26]. Metcalf [38], exposes the temperature relationship under two conditions from the integration of the Arrhenius model (2), known as the Van’t Hoff-Arrhenius relationship (3). Several authors [20, 37, 39, 40] mentioned Arrhenius model and suggested it for the estimation of kinetic constants. Metcalf [38] indicates that this relationship is a simplification of the Arrhenius model, in which the activity coefficient (θ) is a constant that contains activation energy (Ea), ideal gas constant (R), a reference temperature (To), and operation temperature (T). The bibliographic search did not reflect evidence on methodologies that relate HRT and temperature as design and operating parameters in continuous AD reactors. Therefore, this research evaluates the behavior of kinetic constants concerning temperature using the Arrhenius model and the Van’t Hoff-Arrhenius relationship, with projection towards estimating the hydraulic retention time in continuously stirred tank reactors.
2. Materials and Methods2.1. Kinetic AssessmentThe kinetic model was the first-order (1):
Where: B is the methane yield [NmL gVS−1] at time t; B0 is the maximum methane yield [NmL gVS−1]; k is the first-order kinetic constant of reaction [d−1], and t is the digestion time [d]. The models for evaluating the effect of temperature on the kinetic coefficients were the Arrhenius model (2) and Van’t Hoff-Arrhenius relationship (3):
Where: kT is the kinetic rate constant at reaction temperature, first-order k [d−1]; A is the pre-exponential factor [d−1]; k0 is the kinetic rate constant at reference temperature [d−1]; Ea is the activation energy [kJ mol−1]; R is the universal gas constant [kJ mol−1 K−1]; T is the reaction temperature [K]; T0 is a reference temperature [20°C]; θ is the temperature activity coefficient [dimensionless], and T is the reaction temperature [°C].
2.2. Model ImplementationThe estimation of the temperature effect on the anaerobic digestion of organic waste consisted in the evaluation of the capacity of the Arrhenius (2) and Van’t Hoff (3) models to adapt to the variations of the constant k reported by the first-order kinetic model (1). The data for evaluating the models came from scientific articles that used BMP tests to evaluate organic substrates at three temperature levels. The organic substrates evaluated from the literature were macroalgae (MA) [32], swine manure (SM) [41], and chicken manure sawdust (CMi,j) mixed with unpretreated Miscanthus or fungi pretreated Miscanthus with Pleurotus ostreatus or Trametes versicolor [42]. The subindex i stands for the different mixture proportions of chicken manure sawdust with unpretreated or pretreated Miscanthus (1 = 80:20, 2 = 60:40, 3 = 50:50). The subindex j stands for the co-substrate (1 = Pleurotus ostreatus pretreatment; 2 = Trametes versicolor pretreatment; 3 = unpre-treated Miscanthus). Table 1 reports the relevant information of the reported data.
Curve Fitting Toolbox 3.5.13 from the Matlab R2021a was the software for fitting the model. The statistical criteria for the evaluation of the model were root-mean-square error (RMSE) and the sum of squares errors (SSE) [20].
2.3. Hydraulic Retention Time EstimationArango-Osorio et al. [25] related the reaction volume (V) in stirred tank-type reactors with the HRT. The HRT estimation in continuous stirred-tank reactors considers a substrate degradation rate defined by a kinetic law [24, 43]. On the other hand, the HRT evaluation (4) uses the mass balance of semi-continuous reactors [23, 44].
Where: B is the methane yield [NmL gVS−1] at time t; B0 is the maximum methane yield [NmL gVS−1]. The evaluation of (4) used 80% of B0.
Kafle et al. [45] evaluated the time to produce a fraction between 80 (T80) and 90% (T90) of the observed maximum methane yield in batch reactors as an estimator of HRT in continuous reactors. This study analyzes T80 and T90 using (1) as an indicator of HRT. The clearance of the time variable in the kinetic model led to expression (6):
The determination of T80 used: (i) the constant k reported in Table 1, and (ii) the estimates from the Arrhenius and Van’t Hoff models.
3. Results and Discussion3.1. Evaluation of the Kinetic ConstantsThe Arrhenius model and the Van’t Hoff-Arrhenius relationship described the behavior of the kinetic rates (Table 2). The SSE and RMSE criteria indicated that the Van’t Hoff-Arrhenius relationship introduced fewer estimation errors. The Van’t Hoff-Arrhenius relation is the integrated Arrhenius expression [38], so the adjusted constants have similar phenomenological meanings. However, Van’t Hoff-Arrhenius relationship discards the constant A (associated with the collision between particles and is independent of temperature), instead, this model estimates the constant k0, which acquires values near kT.
The fit of first-order k to the Arrhenius model presented A values between 3.81×102 and 3.45×103 d−1. Almeida Streitwieser et al. [24] reported A values of 2.45×102 d−1 for organic wastes from the agribusiness in the mesophilic regime. The fitted values of Ea in the mesophilic range (25–45°C) were among 11.3 and 48.6 kJ mol−1. Thus, the results agreed with the results of Almeida Streitwieser et al. [24], who reported an Ea value for the mesophilic temperature regime (8.88 kJ mol−1) lower than the thermophilic regime (116.55 kJ mol−1). Li et al. [46] proposed that Ea in the anaerobic digestion process is the energy required to overcome the energy barrier and initiate the reaction, with values from 30 to 300 kJ mol−1.
According to the evaluated kinetic model, the Van’t Hoff-Arrhenius relationship establishes a reaction rate constant (k0) at a reference temperature. The results obtained for the first-order model rate constants were close to the reported values of k. The temperature activity coefficient was among 1.01 and 1.12, Deng et al. [39] estimated θ through an analysis of the kinetic constants and temperatures concerning the Van’t Hoff-Arrhenius relation:
Where: kT1 and kT2 are the kinetic rates estimated constants at temperatures T1 and T2, respectively. The literature used ten (10) combinations of temperatures between 15 and 35°C, with a temperature step (ΔT) of 5°C, and reported θ among 1.028–1.332, for swine wastewater AD, and identified a decreasing trend concerning to temperature increases. The highest θ was for the combination of 15–20°C. The combinations of temperatures over 20°C estimated similar θ (~ 1.03 to 1.04). The similarity between the values proposed in the literature and this study establishes that estimating of k0 (at T = 20°C) by non-linear regression is a viable alternative for temperature analysis. The statistical criteria SSE and RMSE evaluated the sums of the errors introduced by the analyzed model. These criteria analyze the entire model and indicate a good fit. However, the comparison of the estimated kinetic constants with the observed (Fig. 1) shows slight deviations of the models. Even though the Van’t Hoff-Arrhenius relationship reported lower SSE and RMSE than those presented for the Arrhenius model, the variations of the estimated k for each substrate and temperature (Fig. 1) were more significant.
Variations in the predicted rate constants concerning to observed may be due to inoculum-substrate ratio [47], the composition of the substrates [48, 49], and ΔT [26, 50]. Membere et al. [32], Chae et al. [41], and Pečar et al. [42], which evaluated diverse organic matters, did not evaluate the variations of the inoculum-substrate relationship. Furthermore, Pečar et al. [42] evaluated co-digestion alternatives of chicken manure sawdust with Miscanthus (pretreated and unpretreated) and did not report significant differences in the kinetic behaviors in methane production for the mixtures.
The temperature ranges for the evaluation of MA, SM, and CM were between 25 and 45°C, however, ΔT was different in each investigation. Membere et al. [32] evaluated the effect of temperature on the anaerobic digestion of MA with ΔT of 10°C. Chae et al. [41] used a lower ΔT (5°C) for SM digestion. In the case of CM, Pečar et al. [42] used a variable ΔT of 5 and 2°C. Dalby et al. [50] mention that the Van’t Hoff-Arrhenius relationship underestimates the methane production because the model did not evaluate the composition of the anaerobic consortia and the variability concerning time and temperature. Using ΔT over 5°C is a risk because the metabolic behavior of anaerobic consortia is sensitive to temperature [26]. Furthermore, variations in T cause accumulations of volatile fatty acids that decrease methane yield [51]. Mesophilic inoculums have a better capacity to adapt to temperature changes than thermophilic inoculums [52].
3.2. Hydraulic Retention Time Estimation
Eq. (5) used the first-order constants at evaluated temperatures estimated using the Arrhenius model and Van’t-Hoff-Arrhenius relationship. The HRT estimated at 80% of the maximum methane yield in CSTR (Fig. 2) reached values above 100 d for substrates with first-order constants below 0.03 d−1.
Fig. 2(a) presents the HRT evaluated for the constants observed for the substrates in the different temperature conditions. MA reported the lowest observed k (0.02d−1) for its lower temperature level concerning the other observations, this led to the highest value of HRT (200 d). For SM, the differences between HRT at different temperatures were less than 21 d. The CM variants indicated that the differences between the HRT calculated for the temperature interval between 35 and 40°C did not exceed nine days (with differences of up to 0.46 d). Likewise, for the levels between 40 and 42°C, the differences were up to 5.77 d (with minimum values of 2.22 d). According to the observed values (Fig. 2(a)), HRT decreases with the increase in T (and the increase in k). The Arrhenius model (Fig. 2(b)) indicated HRT values with differences for MA of 112d at T = 25°C that decreased to 14 and 2.50 d for 35 and 45°C, respectively. The evaluation of SM and CM by the Arrhenius model indicated a maximum difference of 14 d and a minimum of 0.02 d between all the evaluated cases. The Van’t Hoff-Arrhenius (Fig. 2(c)) relationship reported a different behavior for SM and MA, because this model contains an exponential term (θ(T−T0)), which shows the increase in k concerning the increase in T, provided that θ over 1. Although the kinetic evaluation proposed in the literature is correct, and the Van’t Hoff-Arrhenius relationship presented a satisfactory adjustment of the kinetic constants, the T intervals tested led to θ values of 0.93 and 0.95 for MA and SM, respectively. This evidence indicates that the application of the Van’t Hoff-Arrhenius relationship was deficient and confirms that its use is not convenient in estimating HRT for T intervals over 5°C.
Arango-Osorio et al. [25] evaluated different designs of anaerobic reactors, using as general sizing equation:
Where: Vrxn is reaction volume [m3]; u is the inlet volumetric flow of the waste [m3/d]. The calculation of Vrxn depends on fixed values of HRT and u [40], however, the variation of the temperature regime decreases the methane yield and affects the kinetic constant due to the accumulation of volatile fatty acids [51–56]. Thus, a fluctuation of the temperature in the operation of continuous reactors can cause problems related to the variation of HRT.
Ziganshin et al. [55] observed that the reduction of HRT affects the structure of the methanogenic community and produced a drop of around 48% in the activity of the microorganisms. Dareioti et al. [57] indicated that the decrease in HRT negatively affects methanogenesis due to the accumulation of volatile fatty acids (mainly acetic acid). The accumulation of acetate occurred by inhibition of acetoclastic methanogenesis and the accumulation of propionate by inhibition of acetogens [58]. Furthermore, low HRT led to the elimination of acetotrophic organisms due to washout and the proliferation of hydrogenotrophic organisms [59].
Li et al. [58] evaluated the variation of HRT in methane yield in continuous reactors. The lowest HRT presented higher methane productions and accumulation of volatile fatty acids. Likewise, increases in HRT cause a decrease and stabilization of methane production and a decrease in propionic and acetic acid concentrations. Algapani et al. [60] presented similar results of methane production in a continuous reactor with HRT variations from 30 to 8 days, at a temperature of 35°C. The methane yields at HRT for 30, 20, and 15 days increased slightly as 512.7, 519, and 526 mL/gVS, respectively. After the 15-day HRT values, methane yields decreased. The results presented by Kim et al. [56], noted that increases in temperature and HRT in continuous reactors benefited the methane yield and indicated that methane production decreased with the 2-day increase in HRT.
The HRT evaluation with the constants estimated with the Arrhenius model (Fig. 2(b)) and the Van’t Hoff-Arrhenius relationship (Fig. 2(c)) showed similar behaviors as the HRT calculated with the observed constants. However, the errors introduced by the Arrhenius model and the Van’t Hoff-Arrhenius relationship produce errors in the HRT calculation. The co-digestion variants, CM, present estimated HRT values similar to the observed. The HRTs calculated for CM at low and medium temperatures with the Arrhenius model were lower than the observed (contrary to the results obtained with the Van’t Hoff-Arrhenius relationship).
3.3. Technical Digestion Time as HRT EstimatorThe literature use T80 and/or T90 as an estimator of HRT [21, 22, 45, 61]. The estimations with observations that fit first-order kinetics [21] and cone model [61] reported a lower difference between the observed and calculated values. The modified Gompertz [22, 45] did not show a relationship with T80calc and T90calc because the model refers to a delay in methane production. This research estimated and plotted T80 and T90 from the first-order model (6,7) (Fig. 3) and established a decreasing behavior concerning the increase of k.
The kinetic behavior of methane production is relevant for the identification of T80 and T90 (Fig. 3), with a progressive reduction of the distance between T80 and T90. From k 0.13d−1 (Fig. 3), the differences between T90 and T80 are less than 5.4 d, and estimation errors below 0.005 d−1 cause increases of 3.7% and decreases of 4% in the estimates of T80 and T90.
Although this research proposes a decrease between T80 and T90 for values of k above 0.13 d−1 with estimation errors less than 0.005d−1, the literature presents values of k between 0.019 and 0.13 with estimation errors between 0.002 and 0.01 d−1 [62–64]. The estimates of T80 and T90 depend on the value of k and the spread of the estimation error (10,11).
Where: Δk is the estimation error of k; ΔT80 and ΔT90 are the estimation errors due to the propagation of the calculation error of T80 and T90 corresponding to the estimation with k. Thus, for example, the first-order kinetic constants and the estimation errors for the anaerobic co-digestion of spirulina and switchgrass (33:67) at 37 and 50°C were 0.06±0.003 and 0.13±0.004 d−1, respectively [64]. The estimate of T80 in the thermophilic case was 12.38±0.38 d unlike the mesophilic one, which indicated a value of 26.82±1.34 d. The ΔT80 for the mesophilic case indicates a gap of 1.34 d in T80; this is due to the propagation of the estimation error of k. The observations suggest that Δk should be below k/10 to obtain ΔT80 and ΔT90 lower than 8.40 and 12.11 d, respectively, for k over 0.019 d−1.
A graphical analysis of (5–7) (Fig. 4(a)) established that T80 y T90 underestimate HRT. The differences between HRT concerning T80 and T90 (Fig. 4(a)) for k above 0.13 d−1 are less than 19 and 14 d. This difference decreased to 7 and 5 d for k above 0.355 d−1. However, the trends are similar, and it was possible to establish the ratio factors HRT/T80 (2.4853) y HRT/T90 (1.7371), constant throughout the evaluation interval of k. The estimation error for HRT (ΔHRT) behaves similarly to that proposed for T80 and T90; however, due to the values of HRT are higher than T80 and T90, ΔHRT increases with the Δk. Table 3 presents some estimates of T80, T90, and HRT, for hypothetical cases of k.
The previous observations established that the HRT calculation is less sensitive to k estimation errors (Fig. 4(b)). The differences between the defined HRT values for observed k (kobs) and calculated k (kcal) decrease with increments of k.
4. ConclusionsThis investigation used kinetic data at three levels of temperatures within the mesophilic regime. The Arrhenius model and the Van’t Hoff-Arrhenius relationship adjusted satisfactorily to the data. The fitting coefficients A, Ea, and θ were similar to the reported in the literature. The best results were for data evaluated with ΔT above 5°C, and for the variants that evaluated co-substrates.
The behavior of the methane production kinetics of a substrate determines the HRT calculation. The model for the calculation of HRT presented an inversely proportional dependence with k. The HRT trend showed similarities with T80 and T90. These observations indicate that errors in the estimation of k influence the calculation of HRT and decrease for values of k above 0.13 d−1. The calculation of HRT, T80, and T90 must consider a design of experiments that evaluates the kinetics of methane production in BMP assays at least three temperatures within the same thermal regime, whether within the psychrophilic (< 22°C), mesophilic (25–45°C) or thermophilic regime (50–70°C). This experimental design will show the tendencies of progressive increases of the kinetic constant up to a maximum point and subsequent decrease. Furthermore, to reduce the estimation error of the kinetic parameters, the temperatures of the experiment design will have a separation below 5°C.
AcknowledgmentsThis research is part of the project: “Estimation of methane yield in organic waste mixtures” PYTDOC1796-2019-FCMFQ0025, corresponding to the Universidad Técnica de Manabí.
NomenclatureEa Activation energy [kJ mol−1] kcal Calculated constant [d−1] CSTR Continuous stirred tank reactor - k First-order kinetic constant [d−1] HRT Hydraulic retention time [d] R Ideal gas constant [kJ mol−1 K−1] kt Kinetic rate constant at reaction temperature [d−1] k0 Kinetic rate constant at reference temperature [d−1] kT1 Kinetic rates estimated constant at temperature T1 [d−1] kT2 Kinetic rates estimated constant at temperature T2 [d−1] B0 Maximum methane yield [NmL gVS−1] B Methane yield [NmL gVS−1] kobs Observed constant [d−1] A Pre-exponential factor [d−1] V Reaction volume [m3] T0 Reference temperature [°C] RMSE Root-mean-square error - SSE Sum of squares errors - T Temperature [°C] or [K] θ Temperature activity coefficient - T80 Technical digestion time for the 80% of B0 [°C] T90 Technical digestion time for the 90% of B0 [°C] ΔT Temperature variation [°C] t Time [d] NotesAuthor Contributions S.C.M.S. (Researcher) bibliographic search, model fitting and wrote the manuscript. R.J.B.C. (Ph.D. Student) developed the theory and idea, data analysis, wrote and corrected the manuscript. Y.G.S (Ph.D. Student) data analysis, correction, wrote and corrected the manuscript. O.P.O (Full-time Associate Professor) research direction, critical review of the manuscript. I.P.R (Full-time Professor) research direction, critical review of the manuscript. References1. Guerrero LA, Maas G, Hogland W. Solid Waste Management Challenges for Cities in Developing Countries. Waste Manag. 2013;33:220–232.
https://doi.org/10.1016/j.wasman.2012.09.008.
2. Gavilanes-Terán I, Jara-Samaniego J, Idrovo-Novillo J, Bustamante MA, Moral R, Paredes C. Windrow Composting as Horticultural Waste Management Strategy - A Case Study in Ecuador. Waste Manag. 2016;48:127–134.
https://doi.org/10.1016/j.wasman.2015.11.026.
3. da Silva Alcântara Fratta KD, de Campos Leite Toneli JT, Antonio GC. Diagnosis of the Management of Solid Urban Waste of the Municipalities of ABC Paulista of Brasil through the Application of Sustainability Indicators. Waste Manag. 2019;85:11–17.
https://doi.org/10.1016/j.wasman.2018.12.001.
4. Liu Y, Sun W, Liu J. Greenhouse Gas Emissions from Different Municipal Solid Waste Management Scenarios in China: Based on Carbon and Energy Flow Analysis. Waste Manag. 2017;68:653–661.
https://doi.org/10.1016/j.wasman.2017.06.020.
5. Zhang A, Venkatesh VG, Liu Y, Wan M, Qu T, Huisingh D. Barriers to Smart Waste Management for a Circular Economy in China. J Clean Prod. 2019;240:118198.
https://doi.org/10.1016/j.jclepro.2019.118198.
6. Caldeira C, Vlysidis A, Fiore G, De Laurentiis V, Vignali G, Sala S. Sustainability of Food Waste Biorefinery: A Review on Valorisation Pathways, Techno-Economic Constraints, and Environmental Assessment. Bioresour Technol. 2020;312:123575.
https://doi.org/10.1016/j.biortech.2020.123575.
7. Wainaina S, Awasthi MK, Sarsaiya S, et al. Resource Recovery and Circular Economy from Organic Solid Waste Using Aerobic and Anaerobic Digestion Technologies. Bioresour Technol. 2020;301:122778.
https://doi.org/10.1016/j.biortech.2020.122778.
8. Gargalo CL, Carvalho A, Gernaey KV, Sin G. A Framework for Techno-Economic & Environmental Sustainability Analysis by Risk Assessment for Conceptual Process Evaluation. Biochem Eng J. 2016;116:146–156.
https://doi.org/10.1016/j.bej.2016.06.007.
9. Lebon E, Caillet H, Akinlabi E, Madyira D, Adelard L. Kinetic Study of Anaerobic Co-Digestion, Analysis and Modelling. Procedia Manuf. 2019;35:321–326.
https://doi.org/10.1016/j.promfg.2019.05.047.
10. Beegle JR, Borole AP. Energy Production from Waste: Evaluation of Anaerobic Digestion and Bioelectrochemical Systems Based on Energy Efficiency and Economic Factors. Renew Sustain Energy Rev. 2018;96:343–351.
https://doi.org/10.1016/j.rser.2018.07.057.
11. Li Y, Chen Y, Wu J. Enhancement of Methane Production in Anaerobic Digestion Process: A Review. Appl Energy. 2019;240:120–137.
https://doi.org/10.1016/j.apenergy.2019.01.243.
12. Achinas S, Achinas V, Euverink GJW. A Technological Overview of Biogas Production from Biowaste. Engineering. 2017;3:299–307.
https://doi.org/10.1016/J.ENG.2017.03.002.
13. Silva Neto JV, Gallo WLR. Potential Impacts of Vinasse Biogas Replacing Fossil Oil for Power Generation, Natural Gas, and Increasing Sugarcane Energy in Brazil. Renew Sustain Energy Rev. 2021;135:110281.
https://doi.org/10.1016/j.rser.2020.110281.
14. Badza T, Tesfamariam EH, Cogger CG. Agricultural Use Suitability Assessment and Characterization of Municipal Liquid Sludge: Based on South Africa Survey. Sci Total Environ. 2020;721:137658.
https://doi.org/10.1016/j.scitotenv.2020.137658.
15. Wang N, Huang D, Zhang C, et al. Long-Term Characterization and Resource Potential Evaluation of the Digestate from Food Waste Anaerobic Digestion Plants. Sci Total Environ. 2021;794:148785.
https://doi.org/10.1016/j.scitotenv.2021.148785.
16. Fu Y, Luo T, Mei Z, Li J, Qiu K, Ge Y. Dry Anaerobic Digestion Technologies for Agricultural Straw and Acceptability in China. Sustain. 2018;10:4588.
https://doi.org/10.3390/su10124588.
17. Li P, Li W, Sun M, Xu X, Zhang B, Sun Y. Evaluation of Biochemical Methane Potential and Kinetics on the Anaerobic Digestion of Vegetable Crop Residues. Energies. 2019;12:26.
https://doi.org/10.3390/en12010026.
18. Raposo F, Fernández-Cegrí V, de la Rubia MA, et al. Biochemical Methane Potential (BMP) of Solid Organic Substrates: Evaluation of Anaerobic Biodegradability Using Data from an International Interlaboratory Study. J Chem Technol Biotechnol. 2011;86:1088–1098.
https://doi.org/10.1002/jctb.2622.
19. Filer J, Ding HH, Chang S. Biochemical Methane Potential (BMP) Assay Method for Anaerobic Digestion Research. Water. 2019;11:921.
https://doi.org/10.3390/w11050921.
20. Baquerizo-Crespo R, Astals S, Pérez-Ones O, Pereda-Reyes I. Mathematical Modeling Challenges Associated with Waste Anaerobic Biodegradability. Advances in the Domain of Environmental Biotechnology Environmental and Microbial Biotechnology. Singapore: Springer; 2021. p. 357–387.
21. Kafle GK, Chen L. Comparison on Batch Anaerobic Digestion of Five Different Livestock Manures and Prediction of Biochemical Methane Potential (BMP) Using Different Statistical Models. Waste Manag. 2016;48:492–502.
https://doi.org/10.1016/j.wasman.2015.10.021.
22. Kafle GK, Kim SH. Anaerobic Treatment of Apple Waste with Swine Manure for Biogas Production: Batch and Continuous Operation. Appl Energy. 2013;103:61–72.
https://doi.org/10.1016/j.apenergy.2012.10.018.
23. Linke B. Kinetic Study of Thermophilic Anaerobic Digestion of Solid Wastes from Potato Processing. Biomass Bioenergy. 2006;30:892–896.
https://doi.org/10.1016/j.biombioe.2006.02.001.
24. Almeida Streitwieser D. Comparison of the Anaerobic Digestion at the Mesophilic and Thermophilic Temperature Regime of Organic Wastes from the Agribusiness. Bioresour Technol. 2017;241:985–992.
https://doi.org/10.1016/j.biortech.2017.06.006.
25. Arango-Osorio S, Vasco-Echeverri O, López-Jiménez G, González-Sanchez J, Isaac-Millán I. Methodology for the Design and Economic Assessment of Anaerobic Digestion Plants to Produce Energy and Biofertilizer from Livestock Waste. Sci Total Environ. 2019;685:1169–1180.
https://doi.org/10.1016/j.scitotenv.2019.06.015.
26. Nie E, He P, Zhang H, Hao L, Shao L, Lü F. How Does Temperature Regulate Anaerobic Digestion? Renew Sustain Energy Rev. 2021;150:111453.
https://doi.org/10.1016/j.rser.2021.111453.
27. Gou C, Yang Z, Huang J, Wang H, Xu H, Wang L. Effects of Temperature and Organic Loading Rate on the Performance and Microbial Community of Anaerobic Co-Digestion of Waste Activated Sludge and Food Waste. Chemosphere. 2014;105:146–151.
https://doi.org/10.1016/j.chemosphere.2014.01.018.
28. Li D, Song L, Fang H, et al. Effect of Temperature on the Anaerobic Digestion of Cardboard with Waste Yeast Added: Dose-Response Kinetic Assays, Temperature Coefficient and Microbial Co-Metabolism. J Clean Prod. 2020;275:122949.
https://doi.org/10.1016/j.jclepro.2020.122949.
29. Deepanraj B, Sivasubramanian V, Jayaraj S. Effect of Substrate Pretreatment on Biogas Production through Anaerobic Digestion of Food Waste. Int J Hydrog Energy. 2017;42:26522–26528.
https://doi.org/10.1016/j.ijhydene.2017.06.178.
30. Lin Q, De Vrieze J, Li C, et al. Temperature Regulates Deterministic Processes and the Succession of Microbial Interactions in Anaerobic Digestion Process. Water Res. 2017;123:134–143.
https://doi.org/10.1016/j.watres.2017.06.051.
31. Lettinga G, Rebac S, Zeeman G. Challenge of Psychrophilic Anaerobic Wastewater Treatment. Trends Biotechnol. 2001;19:363–370.
https://doi.org/10.1016/S0167-7799(01)01701-2
32. Membere E, Sallis P. Effect of Temperature on Kinetics of Biogas Production from Macroalgae. Bioresour Technol. 2018;263:410–417.
https://doi.org/10.1016/j.biortech.2018.05.023.
33. Kumar P, Kumar V, Singh J, Kumar P. Electrokinetic Assisted Anaerobic Digestion of Spent Mushroom Substrate Supplemented with Sugar Mill Wastewater for Enhanced Biogas Production. Renew Energy. 2021;179:418–426.
https://doi.org/10.1016/j.renene.2021.07.045.
34. Kumar V, Kumar P, Kumar P, Singh J. Anaerobic Digestion of Azolla Pinnata Biomass Grown in Integrated Industrial Effluent for Enhanced Biogas Production and COD Reduction: Optimization and Kinetics Studies. Environ Technol Innov. 2020;17:100627.
https://doi.org/10.1016/j.eti.2020.100627.
35. Al-Wahaibi A, Osman AI, Al-Muhtaseb AH, et al. Techno-Economic Evaluation of Biogas Production from Food Waste via Anaerobic Digestion. Sci Rep. 2020;10:1–16.
https://doi.org/10.1038/s41598-020-72897-5.
36. Batstone DJ, Keller J. Industrial Applications of the IWA Anaerobic Digestion Model No. 1 (ADM1). Water Sci Technol. 2003;47:199–206.
https://doi.org/10.2166/wst.2003.0647.
37. Manchala KR, Sun Y, Zhang D, Wang Z-W. Anaerobic Digestion Modelling. Adv Bioenergy. 2017;2:69–141.
https://doi.org/10.1016/bs.aibe.2017.01.001
38. Metcalf L. Wastewater Engineering: Treatment and Reuse. Metcalf & Eddy Inc. New York: McGraw-Hill; 2003. p. 245–281.
39. Deng L, Yang H, Liu G, et al. Kinetics of Temperature Effects and Its Significance to the Heating Strategy for Anaerobic Digestion of Swine Wastewater. Appl Energy. 2014;134:349–355.
40. Amagu Echiegu E. Kinetic Models for Anaerobic Fermentation Processes-A Review. Am J Biochem Biotechnol. 2015;11:132–148.
https://doi.org/10.3844/ajbbsp.2015.132.148.
41. Chae KJ, Jang A, Yim SK, Kim IS. The Effects of Digestion Temperature and Temperature Shock on the Biogas Yields from the Mesophilic Anaerobic Digestion of Swine Manure. Bioresour Technol. 2008;99:1–6.
https://doi.org/10.1016/j.biortech.2006.11.063.
42. Pečar D, Goršek A. Kinetics of Methane Production during Anaerobic Digestion of Chicken Manure with Sawdust and Miscanthus. Biomass Bioenergy. 2020;143:105820.
https://doi.org/10.1016/j.biombioe.2020.105820.
43. Janke L, Leite A, Nikolausz M, et al. Biogas Production from Sugarcane Waste: Assessment on Kinetic Challenges for Process Designing. Int J Mol Sci. 2015;16:20685–20703.
https://doi.org/10.3390/ijms160920685.
44. Ericsson N, Nordberg Å, Berglund M. Biogas Plant Management Decision Support – A Temperature and Time-Dependent Dynamic Methane Emission Model for Digestate Storages. Bioresour Technol Rep. 2020;11:100454.
https://doi.org/10.1016/j.biteb.2020.100454.
45. Kafle GK, Kim SH, Sung KI. Ensiling of Fish Industry Waste for Biogas Production: A Lab Scale Evaluation of Biochemical Methane Potential (BMP) and Kinetics. Bioresour Technol. 2013;127:326–336.
https://doi.org/10.1016/j.biortech.2012.09.032.
46. Li X, Mei Q, Dai X, Ding G. Effect of Anaerobic Digestion on Sequential Pyrolysis Kinetics of Organic Solid Wastes Using Thermogravimetric Analysis and Distributed Activation Energy Model. Bioresour Technol. 2017;227:297–307.
https://doi.org/10.1016/j.biortech.2016.12.057.
47. Blasius JP, Contrera RC, Maintinguer SI, Alves de Castro MCA. Effects of Temperature, Proportion and Organic Loading Rate on the Performance of Anaerobic Digestion of Food Waste. Biotechnol Rep. 2020;27:e00503.
https://doi.org/10.1016/j.btre.2020.e00503.
48. Rocamora I, Wagland ST, Villa R, Simpson EW, Fernández O, Bajón-Fernández Y. Dry Anaerobic Digestion of Organic Waste: A Review of Operational Parameters and Their Impact on Process Performance. Bioresour Technol. 2020;299:122681.
https://doi.org/10.1016/j.biortech.2019.122681.
49. Meegoda JN, Li B, Patel K, Wang LB. A Review of the Processes, Parameters, and Optimization of Anaerobic Digestion. Int J Environ Res Public Health. 2018;15:2224.
https://doi.org/10.3390/ijerph15102224.
50. Dalby FR, Hafner SD, Petersen SO, et al. Understanding Methane Emission from Stored Animal Manure: A Review to Guide Model Development. J Environ Qual. 2021;50:817–835.
https://doi.org/10.1002/jeq2.20252.
51. Westerholm M, Isaksson S, Karlsson Lindsjö O, Schnürer A. Microbial Community Adaptability to Altered Temperature Conditions Determines the Potential for Process Optimisation in Biogas Production. Appl Energy. 2018;226:838–848.
https://doi.org/10.1016/j.apenergy.2018.06.045.
52. Chapleur O, Mazeas L, Godon JJ, Bouchez T. Asymmetrical Response of Anaerobic Digestion Microbiota to Temperature Changes. Appl Microbiol Biotechnol. 2016;100:1445–1457.
https://doi.org/10.1007/s00253-015-7046-7.
53. Kafle GK, Bhattarai S, Kim SH, Chen L. Effect of Feed to Microbe Ratios on Anaerobic Digestion of Chinese Cabbage Waste under Mesophilic and Thermophilic Conditions: Biogas Potential and Kinetic Study. J Environ Manage. 2014;133:293–301.
https://doi.org/10.1016/j.jenvman.2013.12.006.
54. Gadow SI, Li YY. Development of an Integrated Anaerobic/Aerobic Bioreactor for Biodegradation of Recalcitrant Azo Dye and Bioenergy Recovery: HRT Effects and Functional Resilience. Bioresour Technol Reports. 2020;9:100388.
https://doi.org/10.1016/j.biteb.2020.100388.
55. Ziganshin AM, Schmidt T, Lv Z, et al. Reduction of the Hydraulic Retention Time at Constant High Organic Loading Rate to Reach the Microbial Limits of Anaerobic Digestion in Various Reactor Systems. Bioresour Technol. 2016;217:62–71.
https://doi.org/10.1016/j.biortech.2016.01.096.
56. Kim JK, Oh BR, Chun YN, Kim SW. Effects of Temperature and Hydraulic Retention Time on Anaerobic Digestion of Food Waste. J Biosci Bioeng. 2006;102:328–332.
https://doi.org/10.1263/jbb.102.328
57. Dareioti MA, Kornaros M. Effect of Hydraulic Retention Time (HRT) on the Anaerobic Co-Digestion of Agro-Industrial Wastes in a Two-Stage CSTR System. Bioresour Technol. 2014;167:407–415.
https://doi.org/10.1016/j.biortech.2014.06.045.
58. Li L, He Q, Wei Y, He Q, Peng X. Early Warning Indicators for Monitoring the Process Failure of Anaerobic Digestion System of Food Waste. Bioresour Technol. 2014;171:491–494.
https://doi.org/10.1016/j.biortech.2014.08.089.
59. Bi S, Hong X, Yang H, et al. Effect of Hydraulic Retention Time on Anaerobic Co-Digestion of Cattle Manure and Food Waste. Renew Energy. 2020;150:213–220.
https://doi.org/10.1016/j.renene.2019.12.091.
60. Algapani DE, Qiao W, di Pumpo F, et al. Long-Term Bio-H2 and Bio-CH4 Production from Food Waste in a Continuous Two-Stage System: Energy Efficiency and Conversion Pathways. Bioresour Technol. 2018;248:204–213.
https://doi.org/10.3390/en12020217.
61. Achinas S, Euverink GJW. Effect of Combined Inoculation on Biogas Production from Hardly Degradable Material. Energies. 2019;12:217.
https://doi.org/10.3390/en12020217.
62. dosSantos LA, Valença RB, daSilva LCS, et al. Methane Generation Potential through Anaerobic Digestion of Fruit Waste. J Clean Prod. 2020;256:120389.
https://doi.org/10.1016/j.jclepro.2020.120389
63. Wang K, Yun S, Xing T, Li B, Abbas Y, Liu X. Binary and Ternary Trace Elements to Enhance Anaerobic Digestion of Cattle Manure: Focusing on Kinetic Models for Biogas Production and Digestate Utilization. Bioresour Technol. 2021;323:124571.
https://doi.org/10.1016/j.biortech.2020.124571
64. El-Mashad HM. Kinetics of Methane Production from the Codigestion of Switchgrass and Spirulina Platensis Algae. Bioresour Technol. 2013;132:305–312.
https://doi.org/10.1016/j.biortech.2012.12.183.
Fig. 2Hydraulic retention time. (a) Observed k (b) Arrhenius model (c) Van’t Hoff-Arrhenius relationship. 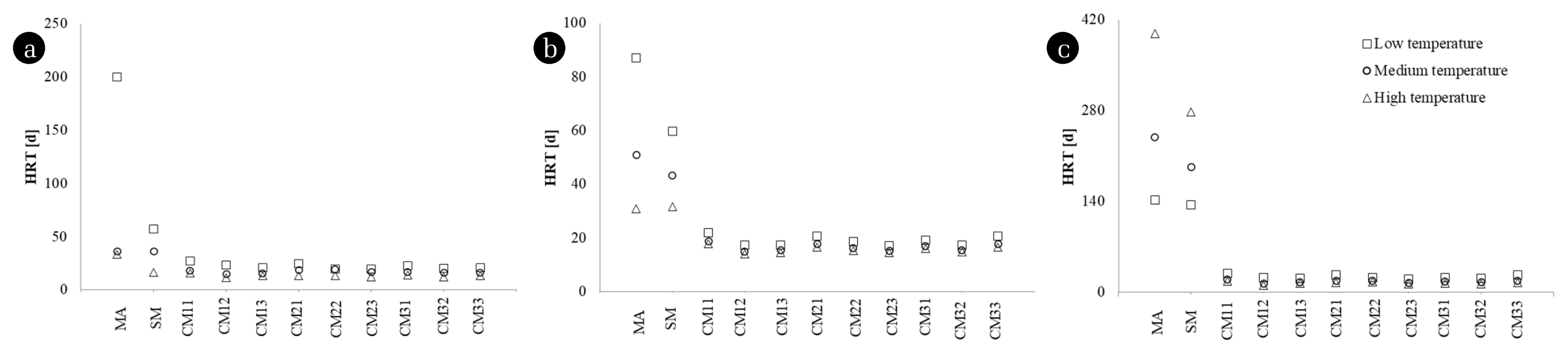
Fig. 3Technical digestion time for various substrates. +,*, ** refer to substrates with fit to the first-order, modified Gompertz and Cone kinetic models. 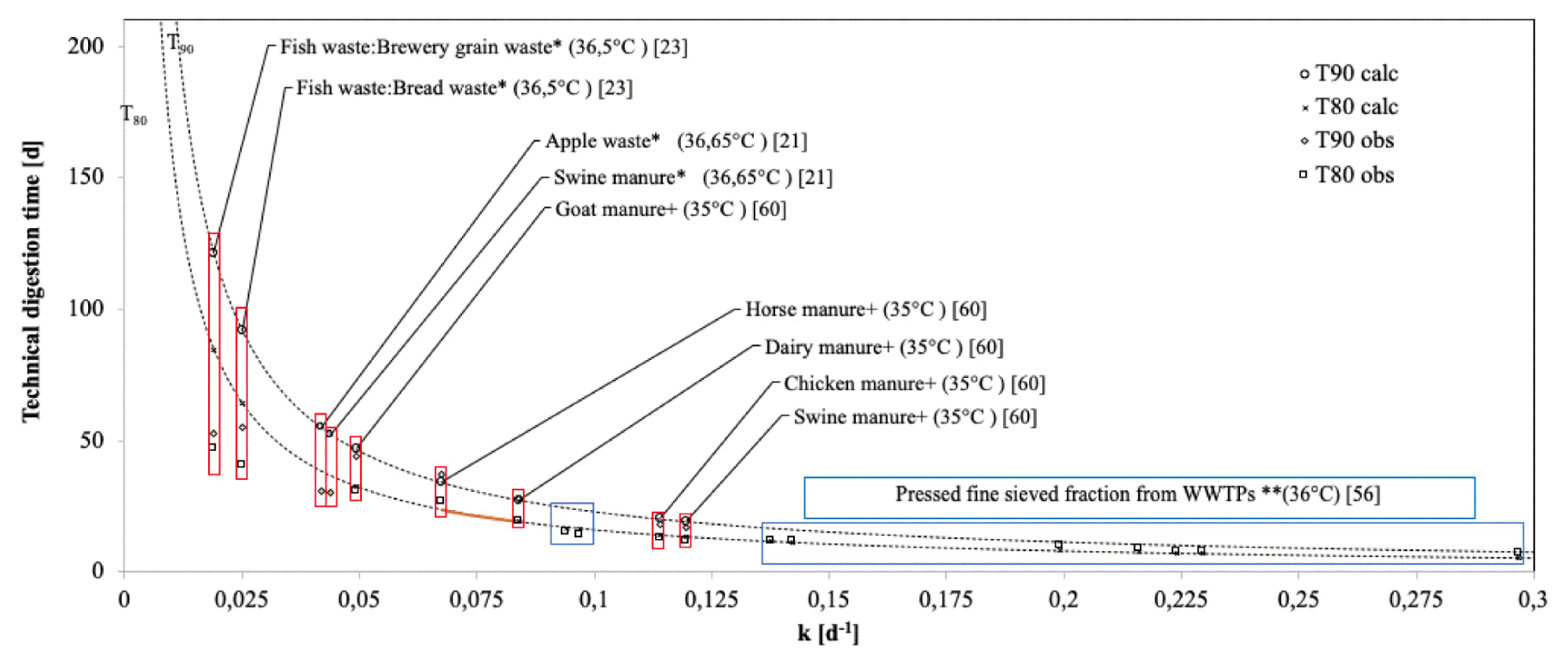
Fig. 4Hydraulic retention time. (a) Comparison of HRT with T80 and T90. (b) Influence of the estimation error of k in the calculation of HRT. 
Table 1Information of Kinetic Constants for Selected Substrates
rough estimation from figures reported in [32]. Table 2Fitted Constants for the Arrhenius Model and the Van’t Hoff-Arrhenius Relationship Table 3Propagation of the Estimation Error in T80, T90 and HRT
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||