AbstractThe effect of the surface charge density of an electret filter on its collection efficiency degradation via isopropyl alcohol (IPA) species exposure is discussed in this study. Five electret filters with different electrostatic properties and identical physical properties were prepared and exposed to IPA species. Furthermore, the filtration performance was evaluated. Filters exposed to IPA droplets showed a drastic reduction in the collection efficiency. In addition, the electret filter with a higher surface charge density had a higher tolerance to IPA droplets, that is, the challenged IPA droplet amount that neutralized the electret filter with a high surface charge density (= 5.0 × 10−5 C/m2) was 2.5 times higher than that of an electret filter with a low surface charge density (= 1.9 × 10−5 C/m2). The results of this study revealed that there was a positive relationship between the surface charge density and challenged amount required to neutralize an electret filter.
1. IntroductionThe COVID-19 pandemic has led to significant changes in the daily lifestyles of humans. People are required to wear a face mask when going out, and there are many restrictions on outdoor activities. According to previous studies, people spend more than 90% of their time indoors [1–3], however this time has increased since the outbreak of COVID-19 [4]. This situation has naturally led to improvements in air quality control to maintain human health. Fine particulate matter is introduced to the respiratory tract during breathing and causes various diseases such as asthma, pneumonia, cardiovascular disease, stroke, and cancer [5–10].
The air purifiers, equipped with electret filters, are generally used to remove particulate matter. Electret filters capture particulate matter effectively because of the strong electrostatic attraction between particles and the charged fiber at low pressure drop [11–18]. In particular, air purifiers are often used in hospitals to provide clean environments for patients. Hand sanitizers and skin disinfectants are frequently used to reduce infection with germs, which contain isopropyl alcohol (IPA), one of the most widely used organic solvents [19, 20]. However, IPA can negatively influence patients because it is highly volatile and can cause a variety of symptoms such as headache, dizziness, vomiting, nausea, and coma [21, 22]. Mar et al. [23] reported that the IPA concentration in the exhaled air of a hospital patient was approximately 2.5 times higher than that of the average person [23]. Furthermore, IPA negatively affects the filtration performance of an electret filter in an air purifier. Kim et al. reported a reduction in collection efficiency in an electrospun meta-aramid filter when exposed to IPA droplets [24]. It is well known that the decrease in collection efficiency is caused by electrostatic charge degradation [24–26].
Many researchers have attempted to elucidate the charge decay mechanism when an electret filtration system undergoes organic solvent exposure [27–29]. Rychkov et al. [27] reported that the charge decay of the electret filter could be attributed to internal charge collapse due to external ion deposition and masking. Biermann et al. [28] found that conductive solvents create conductive pathways around the fibers. Cantaluobe et al. [29] suggested that the charge decay was not the masking phenomenon on the fiber surface caused by the dipoles of the organic solvent, but that the charge collapse occurred because of the movement of the charge itself. Hence, despite various attempts, the charge decay mechanism of the electret filter remains uncertain. However, once charge degradation by IPA exposure occurs (due to the charge movements, or recombination, as suggested by Cantaloube et al. [29]), an electret filter with a high surface charge density may take a longer time to be neutralized than that with a low surface charge density (Fig. 1).
To determine the relationship between the surface charge density and tolerance to an organic solvent, electret filters with different surface charge densities were prepared, and the challenge amount was quantitatively investigated in this study.
2. Experimental Methods2.1. MaterialsThe filtration performance of an electret filter is highly dependent on its physical structure and electrical properties. The filter thickness and fiber diameter were measured using a scanning electron microscope (SEM, JSM-5900, JEOL). The average fiber diameter was obtained by measuring more than 200 fibers using SEM image in Fig. S1. The filter packing density, α was determined by the relationship between the mass of a filter, Wf, the density of the fiber, ρf, and the volume of the filter, V, as shown in Eq. (1).
The physical properties of the test filters used in the experiment are listed in Table S1. The electrostatic effect should be determined while maintaining the physical properties of the filter constant. To determine the effect of surface charge density on the collection efficiency by organic solvent exposure, it is necessary to prepare test filters with different surface charge densities and with the same physical properties. However, it is quite difficult to prepare test filter media with different surface charge densities and the same physical properties. Therefore, a commercial polypropylene electret filter (E&H Co., Ltd., Republic of Korea), manufactured using the melt-blown method, was used as a Filter No. 1. Five electret filters with different surface charge densities were prepared by recharging Filter No. 1 under different charging conditions, such as applied voltage and treatment duration.
2.2. IPA Exposure of an Electret Filter
Fig. 2 shows the experimental setup used to measure both the droplet and vapor of the IPA species exposed to a test filter. Nitrogen gas was introduced into the impinger to generate IPA droplet and vapor at a flow rate of 1 L/min. The impinger was placed in a water bath (BW-20G, Lab Companion) at a temperature of 60°C. The generated IPA droplets were measured using an aerodynamic particle sizer (model 3321, TSI) upstream of the filter. Both IPA droplets and vapors were trapped in Condenser 1 to determine the challenged IPA mass. The condenser was placed in a chiller (CBT-10, Lab Companion, Daejeon, Republic of Korea) set to a temperature of −40°C. IPA droplet and vapor downstream of the filter were collected in condenser 2. The upstream and downstream sampling lines of the filter holder were kept as short as possible to minimize the deposition of IPA droplet and vapor in the tube line. Quantitative IPA amounts were measured using the Karl Fischer method (870 KF Titrino plus, Metrohm) [30], which calculates the amount of IPA by measuring the water concentration in the solution. The IPA purity was determined by measuring the water concentration upstream (condenser 1) and downstream (condenser 2) of the filter. The amount of IPA exposed to the filter was determined by subtracting the amount of downstream IPA from the amount of upstream IPA.
2.3. Filtration Performance of the Test Filters
Fig. 3 shows the experimental setup used to measure the filtration performance of the test filters. Compressed air was passed through a HEPA filter and flowed into an atomizer containing an aqueous NaCl solution (0.3–0.5 wt%). Polydisperse NaCl particles were generated by atomizing an NaCl solution in an atomizer at a flow rate of 3.2 L/min. The resulting droplets were introduced into a tubular furnace (Lindberg/Blue M, Thermo Fisher Scientific Inc.) controlled at 900°C, followed by a diffusion dryer to remove water species. The dried particles were conditioned to make the equilibrium charging state using a soft X-ray neutralizer (XRC-05, HCT CO., LTD, Icheon, Republic of Korea). Monodispersed singly charged particles were produced by passing them through a differential mobility analyzer (model 3081, TSI). The monodispersed uncharged particles were prepared using a soft X-ray neutralizer, then passed through a charged particle condenser. The size of the test particles ranged from 0.03 to 0.3 μm. The collection efficiency was determined by measuring the concentrations upstream and downstream of the filter using a condensation particle counter (model 3775, TSI Inc.). The filtration velocity was controlled at a rate of 1–10 cm/s.
3. Results and Discussion3.1. Estimation of Surface Charge DensityMany researchers have used the theoretical methodology to determine the surface charge density of a meltblown electret filter, where the net surface charge of the filter is almost zero [31, 32]. In filtration theory, uncharged ultrafine particles are captured in an uncharged filter by diffusion and interception capture mechanisms [33–36]. However, the additional dielectrophoretic capture mechanism is dominant when uncharged ultrafine particles pass through a charged filter [36, 37]. Assuming independent collection mechanisms, the following relationship among single fiber efficiencies can be observed. The single fiber efficiency between an uncharged filter and an uncharged particle, ηM is the sum of the single fiber efficiency by diffusion, ηD, and the single fiber efficiency by interception, ηR. In addition, the single fiber efficiency between a charged filter and an uncharged particle, ηInM is the sum of the single fiber efficiency by mechanical collection mechanisms, ηM, and the single fiber efficiency by dielectrophoretic force, ηIn. Therefore, ηIn can be obtained by subtracting ηM from ηInM, as shown in Eq. (4).
Otani et al. [38] suggested the prediction equations shown in Eq. (5) to (7) for the dielectrophoretic force where ηIn is expressed as a function of the dielectrophoretic force parameter KIn.
where hk is the hydrodynamic factor for the Kuwabara flow, ɛp is the permittivity of a particle (= 6.12 F/m), Cc is Cunningham’s slip coefficient, Qf is the surface charge density of an electret filter, dp is the particle diameter, ɛ0 is the permittivity of the vacuum (= 8.85 × 10−12 C2/N·m2), ɛf is the permittivity of a fiber (= 2.2 C2/N·m2), μ is the viscosity of air (= 1.81 × 10−5 N·s/m2), df is the fiber diameter, and u is the filtration velocity.
The following log-penetration equation describes the relationship between the collection efficiency of a filter and single fiber efficiency:
where L is the filter thickness, and E is the collection efficiency of the filter.
The experimental single fiber efficiency, ηInexp, can be obtained using Eq. (10). The ηInexp values determined experimentally under specific filtration conditions were compared with the theoretical values by assuming the surface charge density of an electret filter. In other words, KIn is determined by the physical properties and Qf of an electret filter. However, Qf is an unknown value because there is no direct measurement method available for melt-blown electret filters. The KIn values at specific filtration conditions under the arbitrarily assumed Qf were determined and compared with the theoretical values calculated using Eq. (5) to (7). Qf can be determined where there is agreement between the experimental and theoretical single fiber efficiency values. Several other studies have used this methodology to determine the surface charge density of an electret filter [30, 38–40].
To determine the surface charge density using Eq. (2) to (7), the collection efficiencies of uncharged particles for both charged and uncharged filters are necessary. Because it is difficult to obtain an uncharged filter with the same internal structure as the charged filter, the uncharged filter was prepared by exposing the electret filter to IPA droplets according to the methodology outlined by Kim et al. [24], Xiao et al. [25], and Sachindou et al. [41]. Previous studies indicate that IPA plays a role in faster and more effective charge degradation than other organic solvents [25, 42]. Therefore, IPA (purity: 99.9%) was used to neutralize the test electret filters. It was further diluted using distilled water to precisely measure the amount of challenged IPA.
Fig. 4 shows the collection efficiencies of five electret filters and those of IPA-exposed filters for uncharged particles at a filtration velocity of 5.3 cm/s. As can be seen in Fig. 4(a), electret filters had a high collection efficiency of more than 80%, with whole particle sizes ranging from 0.03 to 0.3 μm. However, the IPA-exposed filters had a drastic reduction in collection efficiency for the test particles (Fig. 4(b)). The reduction in collection efficiency was due to the loss of electrostatic force between the electret filter and the uncharged particles, which can be explained by the shift of the most penetrating particle size (MPPS) to 200 nm [14, 24]. In other words, diffusion and dielectrophoretic force were the dominant collection mechanisms for uncharged particles in electret filtration, which caused a decrease in MPPS [43, 44]. However, neutralization of the charged filter induced an increase in the MPPS.
The surface charge density of an electret filter can be calculated using the collection efficiencies shown in Fig. S2 and the physical properties of the filter. The prediction equations of the single fiber efficiencies due to pure dielectrophoretic force are expressed in Eq. (5) to (7). As can be seen in the equations, single fiber efficiency is a function of the hydrodynamic factor and the dielectrophoretic force parameter. The hydrodynamic factor depends only on the packing density of the filter. However, the dielectrophoretic force parameter is a function of the surface charge density of the filter, particle diameter, fiber diameter, and filtration velocity.
Assuming the surface charge density of an electret filter, the dielectrophoretic force parameters can be determined for the given filtration conditions. Single fiber efficiencies due to the experimentally measured dielectrophoretic force, ηInexp = ηInMexp -ηMexp, were plotted as a function of the dielectrophoretic force parameter and compared with those determined theoretically. The surface charge density assumed to provide the best fit with the theoretical line is the surface charge density of the filter.
Fig. 5 shows a comparison between the experimental and theoretical single fiber efficiencies. The surface charge densities, Qf were 5 × 10−5, 1.9 × 10−5, 3.5 × 10−5, 2.7 × 10−5 and 3.3 × 10−5 C/m2 for Filter No. 1 and Filter Numbers 2, 3, 4 and 5, respectively. The corona-treated filters had relatively lower surface charge densities than Filter No. 1, implying that corona recharging caused charge neutralization to take place. As can be seen in Fig. 4(a), Filter No. 1, followed by Filter No. 3, had the highest collection efficiencies, followed by Filter No. 5, No. 4, and No. 2. The surface charge densities of the test filters were found to follow the same order, as shown in Fig. 5. The test filters had the same physical properties, resulting in the same mechanical collection efficiency. The difference in collection efficiency observed may be attributed to the differing dielectrophoretic forces of the test filters.
3.2. Size Distribution of Generated IPA DropletsQuantitative phase analysis of the IPA species exposed to the test filter is important. Schuldt et al. [41] mentioned that the electrostatic charges in the electret filter were neutralized by saturated IPA vapors under the ISO 16890 standard [41]. However, both droplets and vapors are present when the vapor saturation ratio exceeds unity [45]. Our previous study showed that vapor-phase organic solvents do not influence the neutralization of an electret filter [30]. Therefore, the ratio of liquid phase IPA to IPA species should be quantified to determine the IPA challenge amount to neutralize an electret filter. Fig. 6 shows the size distribution of the generated IPA droplets. As shown in the figure, the mean diameter in the droplet size distribution was 0.75 μm, and the geometric standard deviation was 1.24. The mass of the generated IPA droplets was determined by multiplying the obtained volume by the density of IPA. Based on the calculation results, it was confirmed that IPA droplets occupied 10.2% of the total IPA species.
3.3. Challenged IPA Droplet Amount Required to Neutralize the Electret FilterAs mentioned above, the test filters had different surface charge densities. In addition, we assumed that a filter with a high surface charge density might have a relatively lower decrease in the charge density due to IPA droplet exposure compared to a filter with a low surface charge density. Therefore, the durability of filters with different surface charge densities to IPA droplets was investigated in this study.
Fig. 7 shows the changes in the collection efficiency of the test filters by the challenged IPA amount. As shown in Fig. 6, IPA droplets occupied approximately 10.2% of the total IPA (vapors and droplets). The upper X-axis in the graph shows the total quantity of IPA passing through the test filter, and the lower X-axis shows the quantity of IPA droplets substantially deposited in the test filter. Uncharged particles of 200 nm in size were used in the measurement, as they were found to have the largest difference in collection efficiency (Fig. 4). Each test filter showed a drastic decrease in collection efficiency at a certain challenged IPA amount. The dramatic decrease in collection efficiency of Filter No. 1 appeared at the challenged IPA droplet amount of 8.67 g/m2, compared with 3.47 g/m2 for Filter No. 2, 7.96 g/m2 for Filter No. 3, 6.63 g/m2 for Filter No. 4, and 6.83 g/m2 for Filter No. 5. The amount of IPA droplets challenged to neutralize Filter No. 1 (Qf = 5 × 10−5 C/m2) was approximately 2.5 times higher than that of Filter No. 2 (Qf = 1.9 × 10−5 C/m2). This result indicates that an electret filter with a higher surface charge density is durable in organic solvents. The collection efficiencies of the test filters exposed to an IPA droplet amount larger than the value were almost the same. To compare the lives of the filters exposed to IPA droplets, the collection efficiencies of IPA-exposed filters are plotted in Fig. S3 as functions of the exposure time at the same IPA solution concentration. The filter with a high surface charge density maintained a high collection efficiency, although the filter was exposed to the IPA droplets for a longer time. It can be seen that the durability of filter No. 1 is 2.5 times that of filter No. 2., implying that a higher surface charge density induces a longer filter life.
The relationship between the surface charge density and challenged IPA droplet amount of the test filter is plotted in Fig. 8. As shown in the figure, there is a linear relationship between the surface charge density and the challenged amount required to neutralize an electret filter. This relationship can be expressed as
where Qf is the surface charge density (C/m2), and S is the challenged IPA droplet amount required to neutralize an electret filter (g/m2).
4. ConclusionsFive electret filters with identical physical properties and different surface charge densities were evaluated to discover the relationship between the charge decay degree and surface charge density. The surface charge density of Filter No. 1 (= 5.0 × 10−5 C/m2) was approximately 2.5 times higher than that of Filter No. 2 (= 1.9 × 10−5 C/m2). In addition, the electret filter with the highest surface charge density (Filter No. 1) had a higher challenged IPA amount, that is, the amount required to neutralize the filter was higher than others. Based on the phase ratios of IPA droplets and vapors, the challenged IPA droplet amounts were 8.67 g/m2 for Filter No. 1 and 3.47 g/m2 for Filter No. 2. The former had about 2.5 times the challenged IPA droplet amount compared to the latter. A proportional relationship between the surface charge density and the challenged IPA droplet amount required to neutralize an electret filter was found. The electret filter with a higher surface charge density was found to have a higher resistance to IPA droplets, that is, one of the representative organic solvents. Based on these results, we can conclude that the charging technology in electret filters should be improved to obtain the tolerance to organic species required in the current situation.
AcknowledgmentsThis work was financially supported by the Technology Innovation Program (20005842, Development of industrial heat-resistant air filter technology) funded by the Ministry of Trade, Industry & Energy (MOTIE), Republic of Korea, and the KITECH (Korea Institute of Industrial Technology) R&D Program (kitech EO-20-0022, Development of eco-friendly production system technology for total periodic resource cycle). The authors also appreciate the supply of corona-treated filters from Geumbo Industry Co., Republic of Korea.
NotesAuthor Contributions W.J.L. (Ph.D. student) conducted the research, investigation process, wrote and edited the manuscript. H.B.K. (Ph.D. student) conducted the research, visualized and data curation about the manuscript. H.J.U. (Ph.D) made funding acquisition and reviewed the manuscript. J.H.H. (Professor) supervised the student and advised about the manuscript. M-H.L. (Assistant Professor) supervised the student, concepted, wrote and edited the manuscript. Reference1. Shilton V, Giess P, Mitchell D, Williams C. The relationships between indoor and outdoor respirable particulate matter: Meteorology, chemistry and personal exposure. Indoor Built Environ. 2002;11:266–274.
2. Wei W, Ramalho O, Mandin C. Indoor air quality requirements in green building certifications. Build Environ. 2015;92:10–19.
3. Chao CY, Wong KK. Residential indoor PM10 and PM2.5 in Hong Kong and the elemental composition. Atmos Environ. 2002;36:265–277.
4. Samuel D-A, Jesica F-A, Sonia C-G, Roberto AG-L. Bad air can also kill: residential indoor air quality and pollutant exposure risk during the COVID-19 crisis. Int J Environ Res Public Health. 2020;17(19)7183.
5. Tiittanen P, Timonen KL, Ruuskanen J, Mirme A, Pekkanen J. Fine particulate air pollution, resuspended road dust and respiratory health among symptomatic children. Eur Respir J. 1999;13:266–273.
6. Peng RD, Bell ML, Geyh AS, et al. Emergency admissions for cardiovascular and respiratory diseases and the chemical composition of fine particle air pollution. Environ Health Perspect. 2009;117(6)957–963.
7. Hassanvand MS, Naddafi K, Faridi S, et al. Characterization of PAHs and metals in indoor/outdoor PM10/PM2.5/PM1 in a retirement home and a school dormitory. Sci Total Environ. 2015;527–528:100–110.
8. Brugge D, Simon MC, Hudda N, et al. Lessons from in-home air filtration intervention trials to reduce urban ultrafine particle number concentrations. Build Environ. 2017;126:266–275.
9. Chen C, Ji W, Zhao B. Size-dependent efficiencies of ultrafine particle removal of various filter media. Build Environ. 2019;190:106171.
10. Asikainen A, Carrer P, Kephalopoulos S, Fernandes EO, Wargocki P, Hänninen O. Reducing burden of disease from residential indoor air exposures in Europe (HEALTHVENT project). Environ Health. 2016;15(S35)61–72.
11. Wang J, Tronville P. Toward standardized test methods to determine the effectiveness of filtration media against airborne nanoparticles. J Nanoparticle Res. 2014;16:2417.
12. Sachinidou P, Bahk YK, Tang M, et al. Inter-Laboratory Validation of the Method to Determine the Filtration Efficiency for Airborne Particles in the 3–500 nm Range and Results Sensitivity Analysis. Aerosol Air Qual Res. 2017;17(11)2669–2680.
13. Goel M. Electret sensors, filters and MEMS devices: new challenges in materials research. Curr Sci. 2003;85:443–453.
14. Sae-lim W, Tnthapanichakoon W, Kanaoka C. Correlation for the efficiency enhancement factor of a single electret fiber. J Aerosol Sci. 2006;37(2)228–240.
15. Tsai PP, Schreuder-Gibson H, Gibson P. Different electrostatic methods for making electret filters. J Electrost. 2002;54(3–4)333–341.
16. Motyl E, Lowkis B. Effect of air humidity on charge decay and lifetime of PP electret nonwovens. Fibres Text East Eur. 2006;14(5)39–42.
17. Ji JH, Bae GN, Kang SH, Hwang JH. Effect of particle loading on the collection performance of an electret cabin air filter for submicron aerosols. J Aerosol Sci. 2003;34:1493–1504.
18. Jasper W, Hinestroza J, Mohan A, et al. Effect of xylene exposure on the performance of electret filter media. J Aerosol Sci. 2005;37:903–911.
19. Silvia G, Sara T, Francesca GB, et al. Determination of sevoflurane and isopropyl alcohol in exhaled breath by thermal desorption gas chromatography–mass spectrometry for exposure assessment of hospital staff. J Pharm Biomed Anal. 2015;106:218–223.
20. Ramona T, Cornelia W, Peter E. How irritant are n-propanol and isopropanol? – A systematic review. Contact Dermatitis. 2020;81(1)1–14.
21. Turner P, Saeed B, Kelsey MC. Dermal absorption of isopropyl alcohol from a commercial hand rub: implications for its use in hand decontamination. J Hospital Infection. 2004;56(4)287–290.
22. Church AS, Witting MD. Laboratory testing in ethanol, methanol, ethylene glycol, and isopropanol toxicities. J Emerg Med. 1997;15:687–692.
23. Mar C, Gemma X, Jose MF-R, Juan MS. Breath gas concentrations mirror exposure to sevoflurane and isopropyl alcohol in hospital environments in non-occupational conditions. J Breath Res. 2016;10(1)016001.
24. Kim HB, Lee WJ, Choi SC, Lee KB, Lee MH. Dependence of the fiber diameter on quality factor of filters fabricated with meta-aramid nanofibers. Sep Purif Technol. 2019;222:332–341.
25. Xiao H, Song Y, Chen G. Correlation between charge decay and solvent effect for melt-blown polypropylene electret filter fabrics. J Electrost. 2014;72:311–314.
26. Kim J, Jasper W, Hinestroza J. Direct probing of solvent-induced charge degradation in polypropylene electret fibers via electrostatic force microscopy. J Microsc. 2007;255(1)72–79.
27. Rychkov AA, Cross GH, Gonchar MG. A method for discriminating between 'external' and 'internal' processes leading to voltage decay from electrets in humid conditions. J Phys D-Appl Phys. 1992;25:522–524.
28. Biermann AH, Lum BY, Bergman W. Evaluation of permanently charged electrofibrous filters. In : 17th DOE Nuclear Air Cleaning Conference; 1 Aug 1982; Denver, CO.
29. Cantaloube B, Dreyfus G, Lewiner J. Vapor-induced depolarization currents in electrets. J Polym Sci Polym Phys. 1979;17(1)95–101.
30. Choi HJ, Park ES, Kim JU, Kim SH, Lee MH. Experimental study on charge decay of electret filter due to organic solvent exposure. Aerosol Sci Technol. 2015;49(10)977–983.
31. Romay FJ, Liu BYH, Chae SJ. Experimental study of electrostatic capture mechanisms in commercial electret filters. Aerosol Sci Technol. 1998;28:224–234.
32. Siag AM, Tennal KB, Mazumder MK. Determination of fiber charge density of electret filters. Particle Sci Technol. 1994;12(4)351–365.
33. Hung CH, Leung WWF. Filtration of nano-aerosol using nanofiber filter under low Peclet number and transitional flow regime. Sep Purif Technol. 2011;79(1)34–42.
34. Lee MH, Choi HJ, Kumita M, Otani Y. Present Status of Air Filters and Exploration of Their New Applications. KONA Powder Part J. 2020;37:19–27.
35. Hinds WC. Aerosol Technology: Properties, Behavior, and Measurement of Airborne Particles. 2nd edNew York: Wiley-Interscience; 1999. p. 192.
36. Kanaoka C, Emi H, Otani Y, Iiyama T. Effect of Charging State of Particles on Electret Filtration. Aerosol Sci Technol. 1987;7(1)1–13.
37. Brown RC. Capture of dust particles in filters by linedipole charged fibers. J Aerosol Sci. 1981;12(4)349–356.
38. Otani Y, Emi H, Mori J. Initial collection efficiency of electret filter and its durability for solid and liquid particles. KONA Powder Part J. 1993;11:207–214.
39. Lee MH, Otani Y, Namiki N, Emi H. Prediction of collection efficiency of high-performance electret filters. J Chem Eng Jpn. 2002;35(1)57–62.
40. Kim JC, Otani Y, Noto D, Namiki N, Kimura K. Initial collection performance of resin wool filters and estimation of charge density. Aerosol Sci Technol. 2005;39(6)501–508.
41. Schuldt T, Dauber E, Engelke T, Schmidt F. Air filters for indoor environments: Interlaboratory evaluation of the new international filter testing standard ISO 16890. Indoor Air. 2020;30(3)473–480.
42. Sachindou P, Heuschling C, Schaniel J, Wang J. Investigation of surface potential discharge mechanism and kinetics in dielectrics exposed to different organic solvents. Polymer. 2018;145:447–453.
43. Janssen LL, Bidwell JO, Mullins HE, Nelson TJ. Efficiency of Degraded Electret Filters: Part I - Laboratory Testing Against NaCl and DOP before and after Exposure to WorkplaceAerosols
. J Int Soc Respir. 2003;20:71–80.
Fig. 4Collection efficiencies of (a) electret filters, and (b) IPA exposed filters for uncharged particles. 
Fig. 5Comparison of experimental and theoretical single fiber efficiencies of (a) Filter No. 1, (b) Filter No. 2, (c) Filter No. 3 (d) Filter No. 4 and (e) Filter No. 5. 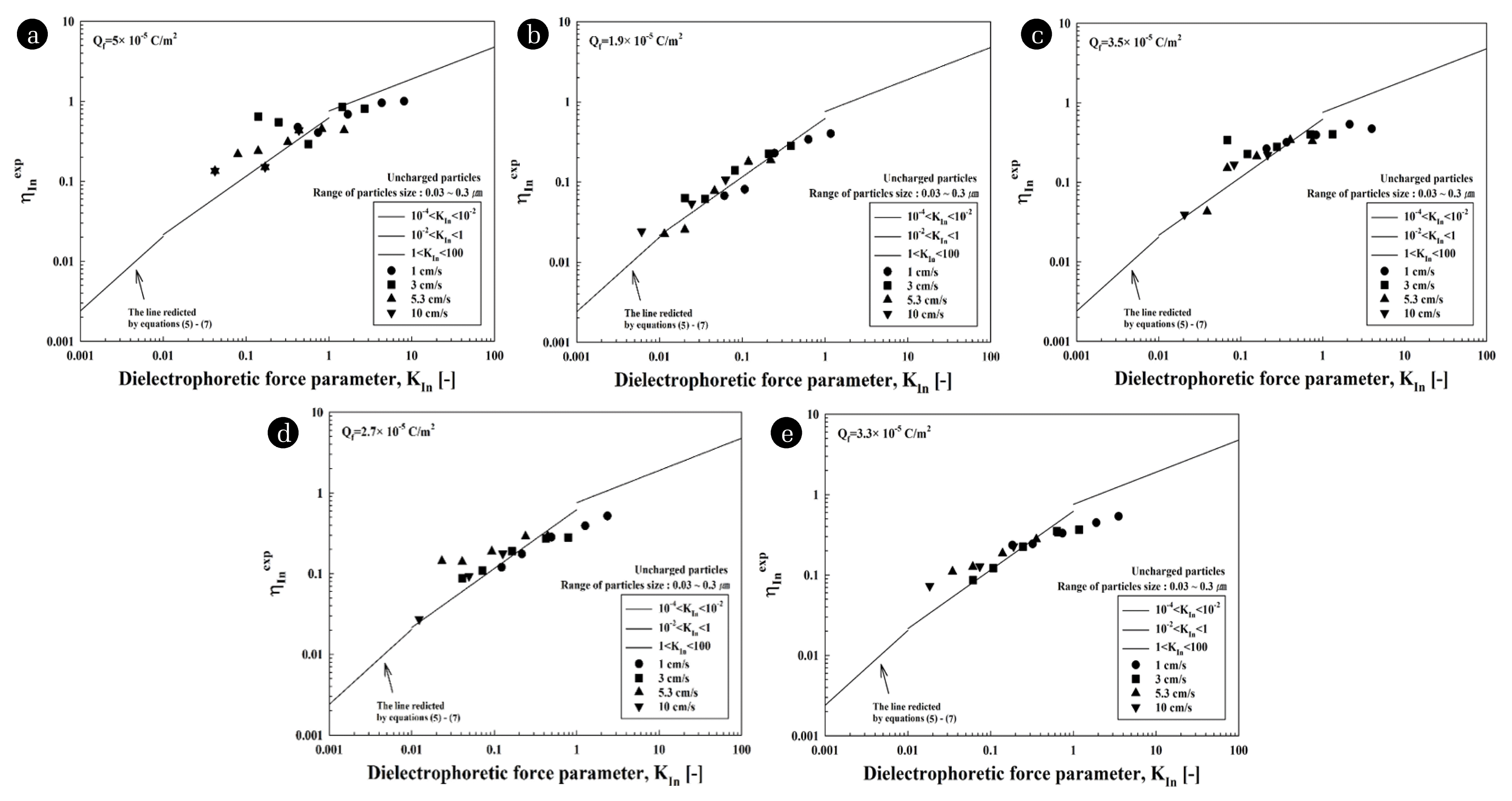
|
|
|||||||||||||||||||||||||||||||||||||||||