Modeling and optimization of small-scale NF/RO seawater desalination using the artificial neural network (ANN)

Asma Adda; Salah Hanini; Salah Bezari; Maamar Laidi; Mohamed Abbas

doi:10.4491/eer.2020.383

Environ Eng Res > Volume 27(2); 2022 > Article

Adda, Hanini, Bezari, Laidi, and Abbas: Modeling and optimization of small-scale NF/RO seawater desalination using the artificial neural network (ANN)

Research

Environmental Engineering Research 2022; 27(2): 200383.

Published online: March 15, 2021

DOI: https://doi.org/10.4491/eer.2020.383

Modeling and optimization of small-scale NF/RO seawater desalination using the artificial neural network (ANN)

Asma Adda^1,^2,^†

, Salah Hanini¹, Salah Bezari², Maamar Laidi¹, Mohamed Abbas³

¹Laboratory of Biomaterials and Transport Phenomena (LBMPT), Faculty of Science and Technology, university of Dr Yahia fares Medea, Algeria

²Unité de Recherche Appliquée en Energies Renouvelables, URAER, Centre de Développement des Energies Renouvelables, CDER, 47133 Ghardaïa, Algeria

³Unit of Solar Equipments Development-UDES/EPST CDER, Head of research department: Cooling Systems and Water Treatment using Renewable Energies-FTEER, Tipaza, Algeria

^†Corresponding author: E-mail: a.docsolaire2017@gmail.com, Tel: +213 774 43 5070

Received July 3, 2020 Accepted March 8, 2021

(open-access):

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract

The performance of seawater hybrid NF/RO desalination plant including permeate conductivity; permeate flow rate and permeate recovery. Under different feed parameters time, inlet temperature, inlet pressure, inlet conductivity and inlet flow rate were modelled by Artificial Neural Network (ANN) back-propagation based on Levenberg–Marquardt training algorithm. The optimal ANN model had a 5-8-3 architecture with a hyperbolic tangent transfer function in hidden layer and linear transfer function at the output layer. The ability of ANN performed model was compared with multiple linear regression (MLR). The results show that MLR is not satisfactory for predicting the performance of NF/RO hybrid desalination process with a correlation coefficient about 0.6. The trained ANN model has presented a good agreement between the prediction and the experimental data during the training with reasonable statistical metrics values (RMSE, MAE and AARD). The coefficient of determination values for the prediction of permeate conductivity, permeate flow rate and recovery by ANN were 0.969, 0.942, and 0.963, respectively. Therefore, the ANN model can successfully predict the performance of NF/RO hybrid seawater desalination plant.

Keywords: Artificial Neural Network (ANN), Conductivity, Flow rate, NF/RO process, Recovery, Seawater desalination

1. Introduction

Reverse osmosis (RO) technology is advanced technology for desalination plants. It accounts for 90% of the total desalination capacity installed worldwide [1, 2]. RO membranes have currently used in a wide range of applications, including brackish/seawater desalination, drinking water treatment and wastewater reuse [3]. The efficiency of RO membranes in various water treatments is often limited due to membrane fouling. However, to reduce or even overcome these limits, several studies have showed that de NF process can be coupled to RO for seawater desalination [4]. Thus, nanofiltration (NF) is a membrane technology that has positioned between RO and ultrafiltration. NF membranes can reduce the ionic strength of the solution. Moreover, hardness, organics, and particulate contaminants can be removed by NF membranes [5].

Integrating NF with RO desalination process may decrease the complexity and cost of desalination plant. However, NF pretreatment has considered a breakthrough for the desalination process. NF offers several advantages such as low operating pressure, high flux, high retention of multivalent anion salts and organic matter, relatively low investment and low operation and maintenance costs [6, 7] and integrated NF with RO could join the advantages from both kinds of membranes [8, 9].

Several researchers have provided to increase the water recovery of RO systems without reducing the membranes life. The performance of NF processes cannot meet drinking water standards because of its inability to reduce salinity in seawater [10, 11].

Many works have been carried out using the NF process for pretreatment, although, the NF permeate quality was excellent, nonetheless the NF permeate water recovery ratio was modest about 50% at an applied pressure of 30 bar [12]. Another advantage, related to the high performance of desalination systems, can be reducing the price of desalted water. Hassan et al. [13, 14] proposed the NF–RO low-cost seawater desalination process. they show that with low pressure of 22 bar, the Ca²⁺, Mg²⁺, SO₄⁻², HCO³⁻ and total hardness rejection of NF were 89.4%, 94.0%, 97.8%, 96.6% and 93.3%, respectively, and the rejection rate of monovalent ions (Cl⁻, Na⁺) was 40.3%, achieving about 27% reduction in the net water production cost through a single-stage SWRO. For the first time, the NF membrane pretreatment process was integrated with one of the conventional desalination processes on a pilot plant in Saudi Arabia. This conception was evaluated on NF–SWRO, NF–MSF, and NF–SWRO–MSF pilot plant units using Gulf seawater [15]. Drioli et al. [16, 17] integrated the MF–NF–RO system with membrane distillation/crystallization (MD/MC) units. To achieve the high water recovery rates of 92.8%. NF is used for pretreatment and load reduction to the following RO unit, a membrane crystallizer completes was used and available waste thermal energy and brine pressure exchanger system. The energy consumption of the NF–RO–MC process was reduced to 1.54–1.61 kWh/m³ and the water cost is reduced to 0.56 $/m³. In seawater desalination process, NF is applied as a pretreatment step of seawater feed and RO or MSF as final treatment step [18]. AlTaee and Sharif [19] carried out the cost analysis on a dual NF-NF, NF-RO and single RO systems. The results showed that NF-NF combination was the lower cost followed by RO then NF-RO systems. In another study, Kaya et al. [20], for applicability of NF membranes prior to the SWRO system was also investigated. They reported that SWRO flux increased from 30.1 LMH to 55.1 LMH when NF was used as a pretreatment prior to seawater SWRO unit (flux of single SW30-RO membrane was 30.1 LMH at 55 bar, while the average flux of the integrated NF90 (30 bar) + SW30-RO (40 bar) system flux was 55.1 LMH). The results showed a good rejection with respect to all ions.

In a recent study, Kaya et al. [21] investigated NF membranes as a pretreatment prior to RO in seawater desalination. The membranes used were NF270 and NF90 as the NF membranes, while the brackish water RO membrane BW30 was used as the RO membrane. The permeate water of the NF membranes was collected and used as the feed to the BW30 membrane.

However, the NF/RO separation process is the most complex operating and control of all major membrane operations [22]. The operating conditions are taken into consideration when modelling a RO/NF membrane system. There are certain factors, which greatly affect the performance of a NF/RO hybrid system. However, the parameters that significantly affects the performance of NF/RO desalination plant are the permeate water quality (conductivity, pH), permeate flow rate, the permeate recovery, the permeability and rejection.

Traditionally, membrane performance has been predicted by polynomial correlations, but the neural network model offers the advantage allowing the user to visualise the entire operation, the capability of learning from the experimental results and obtaining highly accurate findings.

In recent years, the application of ANN for modelling has been greatly increased success in various fields of engineering sciences. Among the methods of linear regression and correlation multivariable widely studied in the 70th, the neural approach allowed the establishment of a model from non-linear relations between inputs and outputs of the process [23].

The use of ANN in the field of desalination with RO technology, it should be noted that since 1993. When El-Hawary [24] proposed some possible applications of ANNs in desalination proposals have been published for the use of ANNs in tasks including optimization the operation of the SWRO desalination plant. Abbas et al. [25] identified the variable of permeate flow rate to be controlled in RO seawater and brackish plant with ANN. Garg et al. [26] used ANN simulation to study the performance of small-scale RO membrane which control the permeate recovery, the TDS and specific energy consumption. Aish et al. [27] considered the permeate flow rate and TDS adequate variables to control and modeling of five large and small scale brackish water plants in Gaza strip.

Madaeni et al. [28] applied the ANN model to predict the permeate flow rate, conductivity which optimize and control of RO water treatment. Recently, Cabrera et al. [29] considered the application of an ANN control system of an RO seawater desalination unit, which predict the pressure, feed flow rate, and permeate flow rate, conductivity.

This paper presents the experimental results obtained from a small scale NF/RO hybrid system conducted by Hamed [30] and developed a method for the simulation of membrane performance by using artificial neural networks. The neural network model successfully predicts the three important parameters on which the NF/RO operation is based i.e. the permeate conductivity, permeate flow rate and permeate recovery.

The aim of this study was to investigate the capacity of an ANN to modeling the performance of NF/RO seawater desalination plant by means of prediction the permeate conductivity, permeate flow rate and permeate recovery. The performance of the ANN models was compared to MLR.

2. Material and Method

2.1. Experimental Data

The Saline Water Desalination Research Institute (SWRI) [30] provided the experimental NF/SWRO desalination plant data used for building the ANN model. A pilot plant testing in which the NF membrane NF product is sent to the RO unit and its brine reject is used as a make-up to the MSF plant, the NF unit received pretreated seawater with a temperature feed varies between 24°C and 34°C and was operated with operating pressure about 24 kg/cm² at a recovery of 53–57%. The SWRO unit that received the NF product as feed the operating pressure was maintained at 60 kg/cm² and a temperature ranged from 23 to 34°C, where the average permeate recovery of the first and second vessels were 30 and 21%, respectively but the overall recovery the SWRO system was about 45%. Fig. 1 shows the diagram of the trihybrid NF/RO/MSF desalination pilot system. The samples of water were collected every hour for a period of two months, the selected parameters including: the feed pressure, temperature, conductivity, flow rate, permeate flow rate and permeate water recovery. The selected experimental inputs and outputs variation presented in Table 1.

2.2. Modeling Development

Using a method to control a simulated NF/RO seawater desalination unit. Two approaches were used to develop the most adequate model for the prediction of permeate conductivity, permeate flow rate and permeate recovery.

2.2.1. Neural network modelling

ANN models were built, to predict permeate conductivity, permeate flow rate and recovery (i.e., target variables) using a back-propagation (BP) based on Levenberg–Marquardt algorithm [31] to establish the relationships between the selected model inputs and the target variables. The information propagates in one direction only the forward direction. Determination of the optimum number of hidden layers and nodes within each layer are real problem, and there is no procedure available to know this for first time. For that, a trial and error approach (multiple runs) was followed to get at the best network architecture [32, 33].

The experimental data used to construct the ANN model for NF/RO seawater desalination plant are summarized in Table 1. A total number of 73 different experiments were employed to predict permeate conductivity permeate recovery and permeate flow rate were divided into training and test subsets. As training subset a number of 60 samples, a percentage of 80% of all available data. For test subset, 13 samples (a percentage of 20%) have been considered. The split of data into training and test subsets was carried out to estimate the performance of the neural network. The neuronal network-training model was developed by means of a program written in MATLAB software. Fig. 2 presents the schematic diagram of an ANN where 5 input neurons were selected at the input layer, 3 output neuron that had been taken at the output layer. The results show that the optimal fully connected ANN was obtained using 8 neurons in the hidden layer, with high R and low RMSE. Different ANN structures with two hidden layers and different neurons in each layer have been tested. It was notable that the ANN with 02 hidden layers can predict the three outputs accurately.

In this investigation, the tangent sigmoid (tansig) as transfer functions was used in the hidden layer (Eq. (1)) and pure linear (purelin) transfer function in the output layer (Eq. (2)). However, the tansig function, produces output in the range of −1 to +1 and the linear transfer function produce outputs in the range of −∞ to +∞ [34, 35].

(1)

Z (x) = \frac{e^{x} - e^{- x}}{e^{x} + e^{- x}}

(2)

Z (x) = x

Whereas normalization is required when there is a difference in the ranges of the input data. In this work, all the training data was normalized between −1 and 1, using Eq. (3) is expressed in the follow:

(3)

x_{n o r m} = \frac{2 (x_{i} - min (x_{i}))}{m a x (x_{i}) - min (x_{i})} - 1

Where x_i is the input or output variable x, x_max and x_min are equal to the maximum and minimum values noted for each variable of x.

2.2.2. Multi-Linear Regression Model (MLR)

The MLR is a simple extension of linear regression, but instead of relating one dependent outcome variable y to one independent variable x, [36, 37].

The MLR model for an outcome variable Y as a function or predictor variables x₁, x₂, and so forth is as follows:

(4)

o u t p u t = x_{0} + Σ_{i = 1}^{n} x_{i} d_{i}

Where x₀ is regression constant, a₀ is a constant (intercept) and x_i the coeffcient of predictorsin linear regression model. MLR calculations were performed using STATISTICA v. 8.0 (Stat Soft, Inc.) software.

2.3. Statistical Performance Evaluation Criteria

In order to evaluate the quality of the prediction of ANN and MLR models, there are set of evaluation criteria such as the coefficient of correlation R, mean absolute error (MAE) and root mean square error (RMSE) [38] for the prediction of permeate conductivity, recovery and permeate flow rate, also the average absolute relative deviation AARD [35, 39]. The equations are expressed in below:

(5)

R = \frac{Σ_{i} (y_{e x p} - \bar{y_{e x p}}) (y_{c a l} - \bar{y_{c a l}})}{\sqrt{Σ_{i} {(y_{e x p} - \bar{y_{e x p}})}^{2}} \sqrt{Σ_{i} {(y_{c a l} - \bar{y_{c a l}})}^{2}}}

(6)

R M S E = \sqrt{\frac{1}{N} Σ_{i = 1}^{N} {(y^{e x p} - y^{c a l})}^{2}}

(7)

M A E = \frac{1}{N} Σ_{i = 1}^{N} | (y_{e x p} - y_{c a l}) |

(8)

A A R D = \frac{1}{N} Σ_{i = 1}^{N} | \frac{y^{e x p} - y^{c a l}}{y^{e x p}} |

Here N is the number of experiments, y_exp is the experimental value for each parameter, y_cal is respectively the predicted value of the i^th experiment calculate by the model for each parameter. and are the arithmetic mean of experimental

\bar{y_{e x p}}

and

\bar{y_{c a l}}

are the arithmetic mean of experimental and calculated values.

In this current work, the artificial neural network was used due to their flexibility to conform to any type of data set and due to their success with various engineering problems [40–45]. Furthermore, the performance of ANN model was validated for extrapolated predictions and the model employed in the research provided the most accurate predictions compared to MLR method.

3. Results and Discussion

3.1. Comparison of the ANN Model and MLR Model

The results of the ANN model and MLR model were evaluated based on the comparison between the model outputs and the experimental data using coefficient of correlation R as shown in Fig. 3. The statistical parameters obtained from the model fits are also summarized in Table 2.

The ANN models resulted in good agreements with the plant data compared to MLR models. Through the analysis of Table 2, the model statistical parameters for the prediction results obtained from using Levenberg-Marquadt program written on MATLAB software. For permeate conductivity R = [0.98 (ANN), 0.622 (MLR)], for permeate recovery R = [0.964 (ANN), 0.572 (MLR)] and for permeate flow rate R = [0.942 (ANN), 0.679 (MLR)].

Through the studies conducted by both madaeni [28] and Cabrera et al. [29] which predicted the permeate flow rate and permeate conductivity, and by comparing the results obtained, it was confirmed that ANN could modelling the both target with accurately.

According to Garg et al. [26] and salami et al. [50] and further confirmation of the permeate recovery prediction of the performance membrane desalination process, the ANN model proposed in this study yielded satisfactory results that can be used as a model for controlling the desalination membrane filtration performance.

In fact, the results show that ANN models were indicated high value of correlation coefficient compared to MLR models. Furthermore, Fig. 4 shows the different statistical parameters obtained for ANN and MLR models. It is observed that for permeate conductivity, permeate recovery and permeate flow rate the MAE, RMSE and AARD values considering more reasonable for ANN models and for MLR models, these statistical parameters are generally considered moderate. Since the neural network model shows good accuracy in predicting these parameters, it could be considerate that the ANN the best-simulated model and is suitable for prediction of seawater desalination performance hybrid process NF/RO in the mean of improving the quality of the water produced and reduce water production costs.

3.2. Mathematical Equations of MLR Developed Model

The models obtained for the prediction of the permeate conductivity, permeate recovery, and permeate flow for the hybrid NF/RO process seawater desalination are linear models according to the subsequent equations:

(9)

δ_{p} = - 301.039 - 0.53 t + 0.635 P + 0.536 T + 0.122 J_{A} + 0.070 δ_{A}

(10)

y = 111.49 + 0.177 t + 0.195 P - 0.28 T - 0.36 J_{A} - 0.30 δ_{A}

(11)

Q_{p} = 2.68 + 0.400 t - 0.0666 P + 0.1792 T + 0.205 J_{A} + 0.129 δ_{A}

3.3. Mathematical Equations of ANN Developed Model

The proposed neural network model successfully predicts the key NF/RO performance parameters i.e., Permeate conductivity, recovery and flow rate for the simulated system desalination. The real prediction power of the ANN model is observed when the simulated and experimental values of the predicted parameters are established as a mathematical function. By integrating all the inputs x_i by the mathematical formula is presented as follow: Knowing that f_h is the Tangent sigmoid transfer function used in hidden layer:

(12)

Z_{j} = f_{h} [Σ_{i = 1}^{5} w_{j i} x_{i} + b_{j}^{h}] = \frac{e x p (Σ_{i = 1}^{5} w_{j i} x_{i} + b_{j}^{h}) - e x p (- Σ_{i = 1}^{5} w_{j i} x_{i} + b_{j}^{h})}{e x p (Σ_{i = 1}^{5} w_{j i} x_{i} + b_{j}^{h}) + e x p (- Σ_{i = 1}^{5} w_{j i} x_{i} + b_{j}^{h})} j = 1, 2, ...... 8

The output H, where f₀ is the pure linear transfer function used in output layer presented as Eq. (18):

(13)

H = f_{0} [Σ_{i = 1}^{8} w_{j i}^{H} Z_{i} + b_{3}^{0}]

Combining Eq. (18) and Eq. (19) for obtain the relation formula of the output parameters of the ANN as follow:

(14)

δ_{p}, Q_{p}, y = Σ_{i = 1}^{8} w_{j i}^{H} (\frac{e x p (Σ_{i = 1}^{5} w_{j i} x_{i} + b_{j}^{h}) - e x p (- Σ_{i = 1}^{5} w_{j i} x_{i} + b_{j}^{h})}{e x p (Σ_{i = 1}^{5} w_{j i} x_{i} + b_{j}^{h}) + e x p (- Σ_{i = 1}^{5} w_{j i} x_{i} + b_{j}^{h})} + b_{3}^{0}

The mathematical equation of the predicted permeate conductivity (δ_p), permeate flow rate (Q_p) and permeate recovery (y) is given by the Eq. (14).

Where j is the number of neurons in the hidden layer (j=8), i is the number of neurons in the input layer (i=5),

w^{I} (w_{(j, i)}^{H})

and

b_{1}^{H}

are weights and bias between input and hidden layer,

w^{H} (w_{(1, j)}^{0})

and

b_{3}^{0}

are weights and bias between hidden and output layer, l is the number of neurons in output layer (l =3).

The model established from ANN to predict the performance of the NF/RO hybrid seawater treatment, including important relevant features that can be easily applied in the optimization of desalination systems.

3.4. Sensitivity Analysis

To assess the performance of NF/RO desalination unit the effect of the individual inputs on the outputs of the system can be studied in ANN. Weights method was employed in this study. The Weights method was proposed initially by Garson [51] and repeated by Goh [52] as a procedure for partitioning the connection weights to determine the relative importance (R_I) of the various inputs. The method essentially involves partitioning the hidden-output connection weights of each hidden neuron into components associated with each input neuron. The relative importance (%) calculated based on Garson equation [53]:

(15)

R_{I j} = \frac{Σ_{m = 1}^{N_{h}} ((\frac{| W_{j m}^{i h} |}{Σ_{k = 1}^{N_{i}} | W_{k m}^{i h} |}) \times | W_{m n}^{h 0} |)}{Σ_{k = 1}^{N_{i}} {Σ_{m = 1}^{N_{h}} ((\frac{| W_{k m}^{i h} |}{Σ_{k = 1}^{N_{i}} | W_{k m}^{i h} |}) \times | W_{m n}^{h 0} |)}}

where I_j is the relative importance of the j^th input variable on output variable; N_i and N_h are the number of input and hidden neurons, respectively; W are connection weights; the superscripts i, h, and o refer to input, hidden and output layers, respectively; and subscripts k, m, and n refer to input, hidden and output neurons, respectively [53]. The numerator of the Eq. (15) describes the sum of the absolute products of the weights for each input.

The relative importance of various variables calculated by Eq. (15) is shown in Fig. 5. As can be seen, all the variables have strong effects on the permeate flow rate, conductivity and water recovery values. Therefore, it can be observed that the highest contribution was obtained with feed pressure (P) about (27%) on all the outputs. Both permeate conductivity and permeate water recovery affected strongly by feed flow (22%). Time and conductivity and temperature have the same influence on all the outputs values about (16%). That explains that the selected inputs parameters have a strong effect on the outputs and a strong significance in the performance of hybrid NF/RO seawater desalination unit.

4. Conclusions

The objective of the present paper was to develop an ANN model able to predict the performance of hybrid NF/RO seawater desalination unit considering the most important inputs variables, namely the feed temperature, the feed pressure, the feed flow rate and feed conductivity. The NN was used for prediction permeate conductivity, permeate flow rate and permeate recovery with the aim of optimization of NF/RO process. Comparison of neuronal network and MLR, revealed that ANN models determination coefficient R for the three outputs is higher than obtained by MLR models as well as satisfactory statistical parameters. However, according to the prediction results, the ANN model was found to have a successful ability to predict The NF/RO process performance seawater desalination compared to the MLR model. In conclusion, it is important to study the system parameters in order to enhance the NF/RO hybrid process and optimize the seawater desalination operation.

In the future works, the models presented in this paper will be used for developing optimization algorithms able to perform optimal designs of a solar-powered NF/RO seawater desalination process facility to be integrated into the plant.

Nomenclature

Time h

pressure Kg/cm²

temperature °C

J_f

Feed flow rate m³/h

δ_f

Feed conductivity μS/cm

δ_p

Permeate conductivity μS/cm

J_p

Permeate flow rate m³/h

permeate recovery %

Acknowledgments

The authors gratefully acknowledge the Algerian Ministry of Higher Education and Scientific Research (CNEPRU Projects Nos. J0102620110007 and J0102620140015) and Laboratory of Biomaterials and Transport Phenomena (LBMPT) of University Yahia Fares of Medea, Algeria.

Notes

Author Contributions

A.A. (Ph.D) conducted all the experiments and wrote the manuscript. S.B. (Ph.D) and S.H. (Professor) interpreted the results obtained and reviewed the article. L.M (Ph.D) realized modelling part and MATLAB programming. M.A. (Professor) revised the manuscript.

Reference

1. Choi Y, Lee Y, Shin K, Park Y, Lee S. Analysis of long-term performance of full-scale reverse osmosis desalination plant using artificial neural network and tree model. Environ Eng Res. 2020;25:763–770.

2. Rodríguez-Calvo A, Silva-Castro GA, Osorio F, López JG, Calvo C. Reverse osmosis seawater desalination: current status of membrane systems. Desalin Water Treat. 2015;56:849–861.

3. Lee E, Lee S, Hong S. A new approach to the characterization of reverse osmosis membrane by dynamic hysteresis. Desalin Water Treat. 2010;18:257–263.

4. Diem XV. Two stage nanofiltration seawater desalination system. United State Patent. 7, 144December 2006. 511–B2.

5. Basile A, Cassano A, Rastogi NK, editorsAdvances in Membrane technologies for water treatment-Materials, Processes and Applications. 1st EditionWoodhead Publishing; 2015.

6. Diawara CK. Nanofiltration Process Efficiency in Water Desalination. Sep Purif Rev. 2008;37:302–324.

7. Hilal N, Al-Zoubi H, Darwish NA, Mohamma AW, Arabi MA. A comprehensive review of nanofiltration membranes: Treatment, pretreatment, modelling, and atomic force microscopy. Desalination. 2004;170:281–308.

8. Fritzmann C, Löwenberg J, Wintgens T, Melin T. State-of-the-art of reverse osmosis desalination. Desalination. 2007;216:1–76.

9. Khawaji AD, Kutubkhanah IK, Wie JM. Advances in seawater desalination technologies. Desalination. 2008;221:47–69.

10. Bellona C, Drewes JE. Role of membrane surface charge and solute physicochemical properties in the rejection of organic acids by NF membranes. J Membrane Sci. 2005;249:227–234.

11. M’nif A, Bouguecha S, Hamrouni B, Dhahbi M. Coupling of membrane processes for brackish water desalination. Desalination. 2007;203:331–336.

12. Hassan AM, Farooque AM, Jamaluddin ATM, et al. Optimization of NF Pretreatment of Feed to Seawater Desalination Plants. In : IDA World Congress on Desalination Water Reuse; 29 Aug–3 Sept 1999; San Diego, USA.

13. Hassan AM, Al-Sofi MA, Al-Amoudi A, et al. A Nanofiltration (NF) Membrane Pretreatment of SWRO Feed and MSF Make-up. In : IDA World Congress on Desalination and Water Reuse; October 6–9 1997; Madrid, Spain. 1997.

14. Hassan AM, Al-Sofi MA, Al-Amoudi A, et al. A new approach to membrane and thermal seawater desalination processes using nanofiltration membrane (part 1). Desalination. 1998;118:35–51.

15. Hassan AM, Al-Sofi MAK, Farooque AM, et al. A nano filtration (NF) membrane pretreatment of SWRO feed and MSF make-up (part 1). In : 4th WSTA Conference; 13–17 Feb 1999; Bahrain. p. 13–17.

16. Drioll E, Criscuoli A, Curcio E. Integrated membrane operations for seawater desalination. Desalination. 2002;147:77–81.

17. Drioli E, Curcio E, DiProfio G, et al. Integrating membrane contactors technology and pressure-driven membrane operations for seawater desalination: energy, Exergy and Costs Analysis. Chem Eng Res Des. 2006;84:209–220.

18. Turek M, Chorążewska M. Nanofiltration process for seawater desalination–salt production integrated system. Desalin Water Treat. 2004;7:178–181.

19. AlTaee A, Sharif AO. Alternative design to dual stage NF seawater desalination using high rejection brackish water membranes. Desalination. 2011;273:391–397.

20. Kaya C, Sert G, Kabay N, Arda M, Yüksel M, Egemen Ö. Pre-treatment of nanofiltration (NF) in seawater Desalination-Preliminary integrated membrane tests in Urla, Turkey. Desalination. 2015;369:10–17.

21. Kaya C, Jarma YA, Guler E, Kabay N, Arda M, Yükse M. Seawater Desalination by using Nanofiltration (NF) and Brackish Water Reverse Osmosis (BWRO) Membranes in Sequential Mode of Operation. J Membrane Sci Res. 2020;6:40–46.

22. Singh R, Tembrock J. Effectively control reverse osmosis systems. Chem Eng Prog. 1999;95:57–64.

23. Suykens JA, Vandewalle JP, De Moor BLR. Artificial neural networks for modelling and control of non-linear systems. 1st edNew York: Springer; 1996.

24. El-Hawary ME. Artificial neural networks and possible applications to desalination. Desalination. 1993;92:125–147.

25. Abbas A, Al-Bastaki N. Modeling of an RO water desalination unit using neural networks. Chem Eng J. 2005;114:1–3.

26. Garg MC, Joshi H. A new approach for optimization of small-scale RO membrane using artificial groundwater. Environ Technol. 2014;35:2988–2999.

27. Aish AM, Zaqoot HA, Abdeljawad SM. Artificial neural network approach for predicting reverse osmosis desalination plants performance in the Gaza Strip. Desalination. 2015;367:240–247.

28. Madaeni SS, Shiri M, Kurdian AR. Modeling, optimization, and control of reverse osmosis water treatment in kazeroon power plant using neural network. Chem Eng Commun. 2015;202:6–14.

29. Cabrera U, Bogdanov D, Breyer C. Chapter 8-Desalination costs using renewable energy technologies. Gude Veera Gnaneswar, editorRenewable Energy Powered Desalination Handbook. Woburn, MA: Butterworth-Heinemann; 2018. p. 287–329.

30. Hamed OA, Hassan AM, Al-Shail , Farooque KMA. Performance analysis of a trihybrid NF/RO/MSF desalination plant. Desalin Water Treat. 2009;1:215–222.

31. Bhagat P. An introduction to neural nets. Chem Eng Prog. 1990;86:55–60.

32. Malinov S, Sha W. Software products for modelling and simulation in materials science. Comp Mater Sci. 2003;28:179–198.

33. Esteban LG, Fernández FG, De Palacios P. Prediction of plywood bonding quality using an artificial neural network. Holzforschung. 2011;65:209–214.

34. Si-Moussa C, Hanini S, Derriche R, Bouhedda M, Bouzidi A. Prediciton of high-pressure vapor liquid equilibrium of six binary systems, carbon dioxide with six esters, using an artificial neural network model. Brazilian J Chem Eng. 2008;25:183–199.

35. Adda A, Hanini S, Abbas M, Sediri M. Novel adsorption model of filtration process in polycarbonate track-etched membrane: Comparative study. Environ Eng Res. 2019;25:479–487.

36. Neil R, malheiser S. Data Literacy: How to Make Your Experiments Robust and Reproducible. 1st Ed3rd chapter:New York: Academic Press; 2017.

37. Sinnakaudan SK, Ghani AA, Ahmad MSS, Zakaria NA. Multiple Linear Regression Model for Total Bed Material Load Prediction. J Hydraul Eng. 2006;132:521–528.

38. Mohamedi B, Hanini S, Ararem A, Mellel N. Simulation of nucleate boiling under ANSYS-FLUENT code by using RPI model coupling with artificial neural networks. Nuclear Sci Technol. 2015;26:40601–040601.

39. Hamadache M, Hanini S, Benkortbi O, Amrane A, Khaouane L, Si Moussa C. Artificial neural network-based equation to predict the toxicity of herbicides on rats. J Chemometr Intell Lab Syst. 2016;154:7–15.

40. Choi Y, Lee Y, Shin K, Park Y, Lee S. Analysis of long-term performance of full-scale reverse osmosis desalination plant using artificial neural network and tree model. Environ Eng Res. 2019;5:763–770.

41. Kaushal NG, Rahul K. Fixed bed utilization for the isolation of xylene vapor: Kinetics and optimization using response surface methodology and artificial neural network. Environ Eng Res. 2021;26:200–105.

42. Muhammad Y, Seung HL. Experimental and neural network modeling of micellar enhanced ultrafiltration for arsenic removal from aqueous solution. Environ Eng Res. 2021;26:190–261.

43. Braimah MN. Comparison of Optimization of Exergy Efficiency of a Crude Distillation Unit Using Artificial Neural Network (ANN) and Response Surface Methods (RSM). J Eng Res Rep. 2020;1–14.

44. Erkaymaz O, Ozer M. Impact of small-world network topology on the conventional artificial neural network for the diagnosis of diabetes. Chaos Soliton Fract. 2016;83:178–185.

45. Morfidis K, Kostinakis K. Seismic parameters combinations for the optimum prediction of the damage state of R/C buildings using neural networks. Adv Eng Soft. 2017;106:1–16.

46. Adeloye AJ. Multiple Linear Regression and Artificial Neural Network Models for Generalized Reservoir Storage-Yield-Reliability Function for Reservoir Planning. J Hydraul Eng. 2009;14:731–738.

47. Heuvelmans G, Muys B, Feyen J. Regionalisation of the Parameters of a Hydrological Model: Comparison of Linear Regression Models with Artificial Neural Nets. J Hydraul Eng. 2006;319:245–265.

48. Thambavani DS, Mageswari TSRU. Application of multivariate linear regression and neural network in the assessment of groundwater quality. Int J Chem Technol Res. 2005;8:1282–1289.

49. Sahoo S, Jha MK. Groundwater-Level Prediction Using Multiple Linear Regression and Artificial Neural Network Techniques: A Comparative Assessment. Hydraul J. 2013;2:1865–1887.

50. Salami ES, Ehetshami M, Karimi-Jashni A, Salari M, Nikbakht SS, Ehteshami A. A mathematical method and artificial neural network modeling to simulate osmosis membrane’s performance. Model Earth Syst Environ. 2016;2:207.

51. Garson GD. Interpreting neural network connection weights. AI Expet. 1991;6:47–51.

52. Goh ATC. Back-propagation neural networks for modeling complex systems. Artif Intell Eng. 1995;9:143–151.

53. Laidi M, Hanini S. Optimal solar COP prediction of a solar-assisted adsorption refrigeration system working with activated carbon/methanol as working pairs using direct and inverse artificial neural network. Int J Refrig. 2013;36:247–257.

Fig. 1

Hybrid NF/RO seawater desalination pilot plant system.

Fig. 2

Schematic diagram of an artificial neural network model.

Fig. 3

Statistical analysis parameters of MLR and ANN models. (a), (c), (e) ANN (b), (d), (f) MLR.

Fig. 4

Statistical analysis parameters of MLR and ANN models.

Fig. 5

The importance percentage distribution of each inputs variable on (a) permeate conductivity (b) permeate recovery and (c) permeate flow.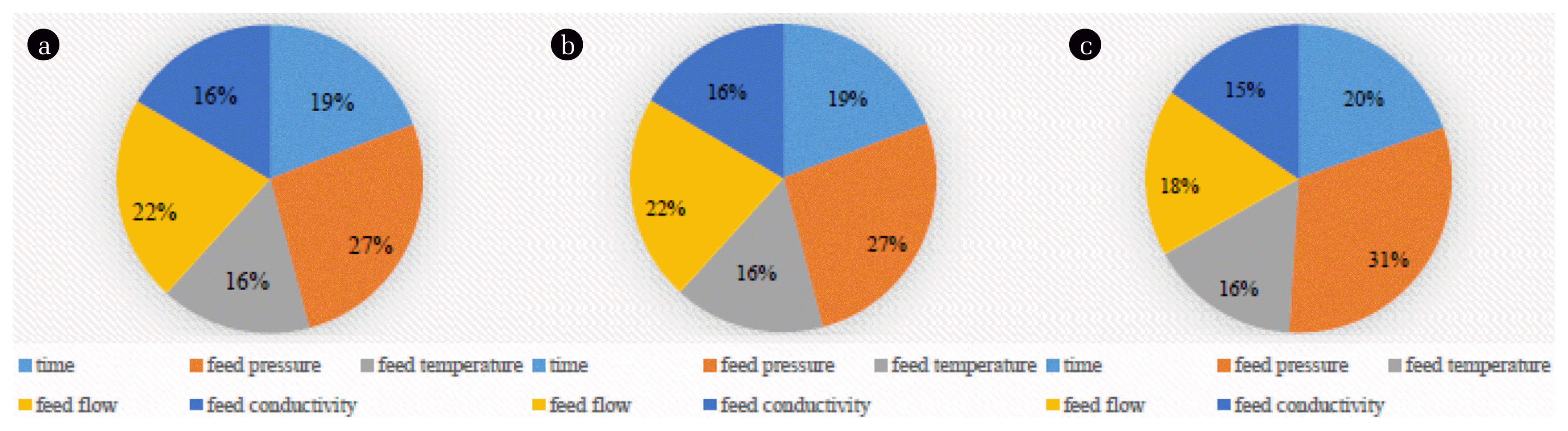

Table 1

Input and the Output Experimental Parameters Extracted with Getdata, Graph, Digitizer Software [30]

	Time (h)	Pressure (kg/cm²)	Temperature (°C)	Flow feed (m³/h)	Conductivity feed (μS/cm)	Permeate recovery (%)	Permeate flow rate (m³/h)	Permeate conductivity (μS/cm)
1	25.197	24.036	25.852	7.817	60,170.213	41.579	1.317	1,117.257
2	37.795	24.3049	25.9193	8.1667	60,777.3	41.0931	1.30732	1,128.32
3	48.294	24.507	25.987	8.014	61,021.277	41.255	1.288	1,128.319
4	71.391	24.036	25.785	7.971	61,234.043	41.093	1.288	1,117.257
5	83.9895	24.0359	25.852	8.2363	61,021.3	40.9312	1.2873	1,139.38
6	94.588	23.901	26.323	7.929	60,382.979	41.255	1.298	1,139.381
7	121.785	23.901	25.785	7.886	60,382.979	44.494	1.385	1,084.071
8	132.59	23.968	25.0448	8.0333	61,061.6	43.5223	1.36585	1,073.01
9	144.882	23.901	23.969	7.628	61,553.191	43.360	1.346	1,073.009
10	167.979	23.767	24.103	7.671	61,765.957	43.360	1.366	1,106.195
11	180.577	23.834	25.718	7.757	61,766.000	43.522	1.376	1,117.260
12	191.076	23.901	27.063	7.800	61,659.574	43.684	1.376	1,139.381
13	216.273	24.507	27.534	7.800	61,234.043	44.008	1.385	1,139.381
14	241.470	24.440	27.466	7.843	61,127.660	44.818	1.424	1,139.381
15	264.567	24.440	27.265	7.800	60,702.128	44.980	1.463	1,095.133
16	287.664	24.440	26.928	7.671	60,808.511	45.951	1.424	1,106.195
17	310.761	24.036	28.005	7.800	61,765.957	44.170	1.385	1,172.566
18	323.36	24.1704	26.9955	7.96667	61,725.1	44.332	1.3561	1,128.32
19	335.958	24.507	25.112	7.586	61,872.340	43.036	1.356	1,095.133
20	361.155	23.969	26.256	7.757	61,021.277	44.818	1.405	1,084.071
21	384.252	24.507	25.987	7.757	60,808.511	44.818	1.395	1,061.947
22	407.349	24.036	25.852	7.628	60,702.128	44.980	1.424	1,039.823
23	419.948	24.2377	25.7848	8.02424	60,595.7	44.9798	1.4218	1,039.82
24	432.546	24.440	26.188	7.714	60,489.362	44.656	1.415	1,050.885
25	455.643	23.901	26.659	7.671	60,489.362	44.656	1.385	1,061.947
26	478.740	24.036	27.130	7.714	60,382.979	45.304	1.434	1,084.071
27	503.937	23.969	27.466	7.757	60,382.979	44.818	1.415	1,128.319
28	527.034	23.969	27.466	7.757	60,276.596	44.170	1.366	1,150.442
29	539.633	26.659	25.987	7.757	60,276.600	44.332	1.376	1,139.380
30	552.231	29.484	27.870	7.757	60,382.979	44.494	1.376	1,150.442
31	575.328	30.493	27.466	7.800	61,127.660	44.494	1.385	1,205.752
32	600.525	29.955	27.534	7.714	60,382.979	44.008	1.366	1,139.381
33	623.622	30.493	29.148	7.800	60,276.596	45.304	1.444	1,250.000
34	636.22	30.2915	28.3408	8.06667	60,019	44.332	1.43415	1,250
35	648.819	30.022	29.619	7.800	59,957.447	44.818	1.424	1,238.938
36	671.916	29.484	29.417	7.671	60,063.830	45.304	1.424	1,216.814
37	697.113	30.022	30.426	7.586	60,063.830	44.980	1.395	1,172.566
38	705.512	30.2242	29.8206	7.9818	59,957.4	44.9798	1.38104	1,194.69
39	720.210	30.493	29.888	7.671	60,063.830	44.494	1.376	1,205.752
40	745.407	30.426	29.955	7.714	59,851.064	45.466	1.424	1,194.690
41	768.504	30.426	29.955	7.757	59,851.064	45.628	1.434	1,095.133
42	791.601	30.493	30.493	7.714	60,063.830	45.142	1.405	1,194.690
43	814.698	31.502	31.166	7.628	60,063.830	45.951	1.483	1,216.814
44	839.895	26.996	30.022	7.800	60,276.596	44.656	1.444	1,227.876
45	852.493	28.2735	3.2915	8.03333	60,208.5	44.9798	1.42439	1,205.75
46	854.593	28.341	29.283	7.714	60,276.600	44.700	1.415	1,183.630
47	865.092	29.283	28.946	7.671	60,276.596	44.332	1.405	1,161.504
48	886.089	29.417	29.014	7.800	60,276.596	45.142	1.405	1,106.195
49	911.286	29.484	28.206	7.800	60,276.596	45.142	1.454	1,073.009
50	936.483	30.022	30.022	7.757	60,063.830	44.818	1.454	1,161.504
51	946.982	31.839	31.839	7.800	60,063.800	44.817	1.446	1,139.380
52	949.081	30.0224	30.4933	8.03333	60,019	44.0081	1.45366	1,139.38
53	959.580	30.022	31.771	7.843	60,063.830	44.818	1.434	1,128.319
54	984.777	30.022	32.646	7.586	60,170.213	44.494	1.434	1,117.257
55	1,007.870	29.484	31.839	7.757	60,170.213	44.656	1.444	1,161.504
56	1,030.970	29.955	33.587	7.714	60,170.213	43.360	1.395	1,128.319
57	1,043.57	29.8879	32.9821	7.9818	60,808.5	43.198	1.38876	1,150.44
58	1,056.170	29.753	28.946	7.800	61,234.043	43.522	1.395	1,161.504
59	1,066.67	29.8879	31.9058	8.03333	61,061.6	44.0081	1.42439	1,117.26
60	1,081.360	29.955	32.444	7.714	60,808.511	44.494	1.454	1,073.009
61	1,096.06	29.8879	31.435	8	60,398.1	44.0081	1.4439	1,117.26
62	1,102.360	29.955	32.444	7.714	60,382.979	44.008	1.434	1,150.442
63	1,127.560	29.552	32.444	7.757	60,170.213	44.008	1.415	1,172.566
64	1,150.660	29.014	32.579	7.757	60,170.213	44.008	1.415	1,150.442
65	1,173.750	29.014	32.713	7.628	60,063.830	44.656	1.463	1,150.442
66	1,201.050	30.022	32.713	7.800	60,170.213	44.170	1.444	1,150.442
67	1,224.150	29.955	33.184	7.628	60,170.213	43.846	1.405	1,161.504
68	1,247.240	30.695	32.915	7.757	60,170.213	44.494	1.444	1,172.566
69	1,270.340	31.031	32.444	7.757	60,382.979	44.494	1.424	1,161.504
70	1,295.540	28.812	32.377	7.586	60,276.596	44.170	1.424	1,172.566
71	1,318.640	29.821	32.780	7.800	60,276.596	44.332	1.434	1,161.504
72	1,331.23	29.417	33.2511	8.0333	60,398.1	44.332	1.4315	1,205.75
73	1,343.830	28.812	33.789	7.843	60,382.979	44.170	1.434	1,238.938

Table 2

Linear Regression Vectors [linear equation: y^predict = αy^exp + β, with α = slope, β = y intercept], R, RMSE, MAE and AARD

		α	β	R	RMSE	MAE	AARD
Permeate Conductivity (μS/cm)	ANN	1.0061	−6.9152	0.9691	11.7	0.6934	0.4571
Permeate Conductivity (μS/cm)	MLR	1.000	0.002	0.622	24.100	29.171	1.531

Permeate Flow rate (m³/h)	ANN	1.0065	−0.0092	0.9422	0.0132	0.0108	0.4583
Permeate Flow rate (m³/h)	MLR	1.00	2.33 10-6	0.679	0.021	0.0246	1.0585

Permeate recovery (%)	ANN	1.0062	−0.2750	0.9636	0.2630	0.2202	0.2977
Permeate recovery (%)	MLR	1.000	−7.560 10-5	0.572	0.316	0.646	0.8842