AbstractLow-cost optical dust sensors are widely used in air purifiers, air conditioners, and air-quality monitoring networks. However, the quality and reliability of these sensors have always been disputed because a standard calibration method has not been established. Low-cost dust sensors used by researchers are calibrated using the researchers’ own methods by applying, for example, a co-location test with reference instruments, a chamber test, or a low-speed duct test. In this study, a test method for the performance evaluation of low-cost sensors was developed using KCl particles with an exponentially decaying particle concentration. With this method, the testing time can be significantly reduced to less than 10 min, and the response characteristics of the sensors to rapidly changing concentrations can be determined. AirAssure from TSI Inc., AirBeam2 from HabitatMap LLC, and DC1100 from Dylos were tested accordingly. The linearities of the measured particulate matter concentrations were significantly good (R2 > 0.95), except for the AirAssure sensors. It was also found that the response characteristics of the sensors depended on the particle concentration decay times.
1. IntroductionLow-cost dust sensors based on scattered light detection have been widely used for measuring concentrations of atmospheric [1–10] and indoor [2, 4, 11, 12] particles. Low-cost sensors can be deployed in a variety of locations owing to their compactness, and large numbers of these sensors can be easily operated to cover a wide area because of their low cost and low energy requirements. Owing to these advantages, particulate matter (PM) concentration monitoring in indoor and outdoor environments and air purifier applications have become new application areas for these sensors [13–16]. The detection principle of these sensors is based on light scattering from particles by using either a light-emitting diode or a laser. However, the quality and reliability of data obtained from low-cost sensors have been disputed [9, 15–17], and even sensor manufacturers and users cannot guarantee the sensor performance because few standard testing methods are available.
Some researchers have performed sensor evaluation tests using low-cost sensors in a group co-located with research-grade reference instruments [1–5, 8, 18], while others have tested sensors by employing particles with known sizes and comparing measured data with reference instrumental observations [19, 20]. Holstius et al. [1] calibrated their low-cost particle sensors using 1-h and 24-h data obtained using a class III US EPA Federal Equivalent Method PM2.5 β-attenuation monitor (BAM-1020, MetOne) during continuous operation at a regulatory monitoring site in California. This co-location calibration method is usually time consuming. A similar co-location test method was employed to calibrate a low-cost PM sensor in the ambient environment over several winters by Kelly et al. [4]. For laboratory calibrations of low-cost sensors, two types of test methods are known, i.e., a chamber method [7, 8, 12, 14, 15, 20, 21] and a low-speed wind tunnel test [4, 13]. In these studies, the low-cost sensors were mostly tested in an environment with uniform and consistent concentration or under a stepwise concentration change. The test method using a constant particle concentration can provide information on the accuracy of the sensor reading at a given particle concentration; however, this method usually requires considerable time to obtain several data points and provides little information about how well the sensor responds to concentration changes. In addition, because most low-cost sensors adopt a moving time average technique for data processing in order to eliminate noise, sensor performance in an environment with rapidly changing concentration is uncertain and needs to be evaluated.
When evaluating the performance of low-cost sensors, the selection of test particles is an important issue. Atmospheric particles feature unknown optical properties, unknown densities, and non-uniform shapes, except for liquid droplets. For these reasons, atmospheric particles might not be suitable as standard calibration particles for optical sensors. However, polystyrene latex particles have been used frequently, especially for optical particle counters, because of their size uniformity and known optical properties. However, because of their high price and, hence, unsuitability for large-volume production, in this study, KCl particles, which are widely used in the calibration of PM sensors, were used for the evaluation of sensor performance. KCl particles are easily accessible, inexpensive, and safe if inhaled. Moreover, the particle size distribution of the KCl particles can be readily adjusted by using different concentrations of KCl solutions when generating test aerosols.
Although previous studies have obtained acceptable performance of low-cost sensors [12, 13, 15, 20, 22], careful sensor calibration procedures and data validation are always needed before and after the use of sensors to ensure unbiased measurement. Even calibrated sensors can provide inaccurate data depending on conditions such as particle concentration, laboratory use, and field measurement [5, 8, 11]. The discrepancies in the measurement results might be caused by the absence of a standardized test method for the sensor manufacturers and end users [9]. There is still a lack of calibration methods for low-cost sensors. In this study, a test method was developed for the performance evaluation of low-cost sensors deploying an exponentially decaying particle concentration in a test duct system. Using this method, the AirAssure (TSI Inc., St. Paul, MN, USA), AirBeam2 (HabitatMap LLC, New York, NY, USA), and DC1100 (Dylos Corporation, Riverside, CA) low-cost sensors were tested. From the results, it is possible to estimate the characteristics of the sensor response to rapidly changing concentrations.
2. Methods2.1. Aerosol Generation and Test Duct SystemsA schematic of the sensor evaluation system is shown in Fig. 1(a). The system consists of two main parts: a test aerosol generation system and a test duct system. In the aerosol generation system, a homemade atomizer is used to generate KCl particles from a 5-wt% KCl solution. The KCl particles are at charge equilibrium by the use of a soft X-ray and are introduced to the particle mixing chamber, where dry dilution air is supplied to mix with the particles. Once the desired particle concentration is achieved in the mixing chamber, the path between the atomizer and chamber is disconnected; thus, no additional particles are introduced, and only clean air is continuously supplied into the chamber. This particle-laden flow is then introduced to the duct system. This process guarantees an exponentially decaying particle concentration in the mixing chamber.
The particles with an exponentially time-decaying concentration are diluted using a second clean air supply system, and the diluted particles are introduced to the test section; a uniform flow is formed using a flow straightener, which has a typical honeycomb structure. The test duct has a rectangular cross-section with dimensions of e470 × 470 mm. This test zone is divided into four equal areas, as shown in the inset “Cross section A-A” of Fig. 1(a). To assess the flow and particle concentration uniformity, flow and concentration measurements were carried out at the center of each quadrant (i.e., Sections 1, 2, 4, and 5 at Cross section A-A) and the center of Cross section A-A (i.e., Section 3 at Cross section A-A). The aerosol mixing chamber and test duct were composed of metal, to minimize the loss of particles adhering to the walls due to static charges. During the test, the temperature and relative humidity were set as 20–22°C and less than 70%, respectively. If the relative humidity exceeds 84.6% (deliquescence relative humidity), the KCl particles transition to the liquid state [23]. Some researchers have reported that, if the operating temperature and relative humidity are high, the dust sensors might not function appropriately [3, 7, 9, 22].
2.2. Mass Balance in the Particle Mixing ChamberA schematic of the particle concentration balance model in the particle mixing chamber is shown in Fig. 1(b). Here, V is the chamber volume, Ci,0 is the initial particle concentration, Qi is the incoming clean air flow rate, C0 is the particle concentration in the incoming air, Qe is the exiting aerosol flow rate, and Ci is the particle concentration of the exiting aerosols at time t. R represents the rate of particle loss caused by particle deposition on chamber walls. With these notations, the rate equation for the particle concentration in the mixing chamber is
where C0 = 0 owing to the particle-free clean air, and R = 0 under the assumption of negligible particle loss in the chamber. Therefore, the particle concentration in the mixing chamber at time t can be expressed as follows:
Here, the incoming clean air flow rate and the exiting aerosol flow rate are the same; on substituting τ = V/Qi, Eq. (2) becomes
Eq. (3) is called the “decaying” exponential function. For the concentration Ci on a logarithmic scale as a function of time t on a linear scale, the plot is a straight line with a slope of −1/τ, and the slope of the decaying particle concentration can be altered by changing the incoming clean air flow rate Qi.
2.3. Validation of the Test Duct SystemThe test system was built by ART+ company (Model ADT-173, Korea) based on the requirements mentioned above. For the uniformity check in the test section, the particle concentration in each quadrant was measured using a Grimm environmental dust monitor (EDM 180, Grimm Aerosol Technik Company, Germany). The Grimm monitor was used as a reference instrument for evaluating the performance of the low-cost sensor. The particle concentration uniformity in the test duct at the five sampling points was found to be significantly good under all different mass concentration conditions, i.e., 50–400 μg/m3, without exceeding ±5% of the mean value, as shown in Fig. S1 in the Supplementary Materials (SM). Each data point is the average value for 1-min measurements.
The size distribution within the exponentially decaying particle concentration is shown in Fig. 2(a). The size distribution of the KCl particles after 0, 1, 2, 3, 4, and 5 min has a geometric standard deviation of approximately 1.51, regardless of the elapsed time. Fig. 2(b) shows the PM2.5 concentrations measured using the reference instrument for 10 min under the decaying particle concentration from approximately 100 to 10 μg/m3. The regression line for the measurements shows excellent exponential decay with a correlation coefficient, R2, of more than 0.97. The test system performance can be easily evaluated by obtaining results similar to those in Fig. 2(b). If the aerosol generation system or the reference instrument does not function appropriately, the regression data for the measurements shown in Fig. 2(b) do not form a straight line on the semi-log graph.
3. Results and Discussion3.1. Performance of Low-cost SensorsFor the performance test of low-cost dust sensors, three models from three manufacturers (AirAssure from TSI, AirBeam2 from HabitatMap, and DC1100 from Dylos) were purchased. To check the unit-to-unit performance variation (or intervariability), three units per model were tested. The tested low-cost dust sensors are listed in Table S1 of the SM. The AirAssure measured PM2.5 mass concentrations. AirBeam2 measured PM1, PM2.5, and PM10 mass concentrations, and the DC1100 measured particle number concentrations in two size ranges: > 1 and > 5 μm.
For the dust sensor performance test, two cases of exponentially decaying aerosol concentrations, i.e., decay times of 3 and 6 min, were used. The particle concentration was set to decrease from approximately 100 to 10 μg/m3. Two decay times were used because some of the low-cost sensors require a long averaging time to handle data internally, and this long averaging time may not ensure accurate measurements of rapidly changing concentrations in the real world. Therefore, with this test, the response characteristics of the sensors to concentrations with different decay rates could be ensured.
Fig. 3(a) shows the PM2.5 concentration measurement data obtained by unit #1 of the AirBeam2 with a 3-min decay time. The blue solid regression line is from the reference instrument data, i.e., the Grimm monitor. The correlation coefficient and slope of AirBeam2 #1 are 0.9443 and −0.0076, respectively. Table S2 in the SM summarizes the results of units #2 and #3 of AirBeam2. The correlation coefficient values for all three units have excellent linearity on the semi-log graph, and the variability between the units is also stable. However, near the low particle concentration region, after an elapsed time of approximately 2 min, the measured concentration starts to deviate from the regression line. The tests were repeated once more, and the results are summarized in Tables S2–S4 in the SM. Furthermore, at a high particle concentration of approximately 100 μg/m3, the concentration obtained by AirBeam2 is approximately 40 μg/m3, i.e., 40% of the reference data value. At a lower concentration of approximately 10 μg/m3, the sensor reading is approximately 7 μg/m3. The tests demonstrate that the overall reading of the AirBeam2 sensors is approximately 40% lower than that of the reference instrument.
To check the response characteristics of the low-cost sensors, the decay time of the particle concentration was increased from 3 to 6 min, indicating a slower decaying concentration. This was done by controlling the clean air flow rate, Qi, supplied to the particle mixing chamber, and the test results of AirBeam2 are shown in Fig. 3(b) and Table S2 in the SM. In general, the sensor readings are quite similar to the 3-min decay case. However, the slope of the regression line is relatively well aligned compared with the faster-decay case. This implies that the sensor response is affected by the rate of concentration change. The ratio of the slope estimated by each low-cost sensor to the slope of the reference data (Table S2 in the SM) was also obtained. A low-cost sensor with a ratio close to 1 indicates that the sensor performs better in terms of the response characteristics. The average ratio for the 6-min decay tests on AirBeam2 was estimated to be approximately 0.7 or more, and this decreased to approximately 0.6 for the 3-min decay tests, i.e., for the faster-decaying concentration.
Before the performances of other tested sensors are discussed, the discrepancy between the absolute concentration value of the Grimm reference instrument and the low-cost sensor at the beginning of the decay region should be mentioned. There might be several reasons for the observed discrepancy. Typically, the calibration of aerosol spectrometers including low-cost dust sensors is achieved by each manufacturer in a different manner. The Grimm dust monitor, used in this study as a reference instrument, is calibrated with traceable monodisperse latex particles certified by the National Institute of Standards and Technology. However, information regarding the calibration process and conditions for the tested low-cost sensors is not certain. They might have been calibrated under different atmospheric conditions with different temperature and humidity ranges. Most low-cost sensors employ optical measurement techniques, including the sensors used in this study [4, 9, 22]. These optical sensors are easily affected by environmental factors [24]. Moreover, low-cost sensors are used for different use cases, each with different performance standards [9]. Therefore, low-cost sensors are calibrated to meet either strict, intermediate, or lower requirements (e.g., accuracy) according to their regulatory standards [25]. Furthermore, the discrepancy might result from a different specification of each sensor in terms of lower and upper detection limits, sensitivity, and sensor-to-sensor variability [26].
Tests with the same procedure were performed with the DC1100 low-cost sensors, and the test results for the 3-min concentration decay case are shown in Fig. 4(a) and Table S3 in the SM. The test results for all three units show a similar trend. The particle number concentrations measured by the DC1100 are higher than for the reference data by several factors, i.e., approximately two times higher at a high concentration of approximately 100 μg/m3 and approximately three times higher at a low concentration of approximately 10 μg/m3. More importantly, the slope of the regression line obtained by the DC1100 under the 3-min decay time is between −0.0102 and −0.0092, and the ratios between the slopes obtained by the DC1100 and reference instrument are more than 0.7.
The same tests were conducted with the concentration decaying for 6 min, i.e., a more slowly changing concentration, and the test results are shown in Fig. 4(b) and Table S3 in the SM. The particle number concentration readings from the DC1100 instrument are approximately 1.5–2 times higher than those of the reference instrument. However, the concentration counts for this slower-decaying-concentration case indicate a better response characteristic to concentration change than the faster-decaying case, as shown in Table S3 in the SM. In other words, the ratios of the measured concentration data to the reference data under the 6-min concentration decay condition were estimated to be approximately between 0.8 and 0.9, which indicates that the DC1100 sensors reflect the concentration changes quite well at this decay rate. The coefficient of determination, R2, for DC1100 is generally higher than that for AirBeam2. However, a direct comparison of these values might result in a misleading measure of the model fit. The number of data points can affect the value of the correlation coefficient. A detailed explanation of the correct use of R2 is well documented in a study by Alexander et al. [27]. Therefore, the values of the obtained coefficients shown in Figs. 3–5 should be considered as the criteria for indicating the relative goodness of model fit, e.g., a good model fit is considered when R2 > 0.9.
The results for the AirAssure sensors are shown in Fig. 5 and Table S4 in the SM. For the AirAssure sensors, the tests were only conducted under the 6-min concentration decay condition. Unlike the previously tested sensors, i.e., AirBeam2 and DC1100, the performance of the AirAssure sensors is difficult to understand, as seen in Fig. 5. In general, the sensor reading increased with the higher particle concentration, and then the measured mass suddenly dropped by almost one order of magnitude. Because of this unusual characteristic, the sensor was not tested under the 3-min decay condition. All units of the AirAssure sensor were tested again, and a similar trend of the sensor readings was found for all the tests. The data for the ratios between the slopes for the AirAssure and reference instrument are in the range of 0.2817 to 0.5493, showing a poor response of the sensor to the concentration change.
To evaluate sensor performance in rapidly changing particle concentrations, the slope of the concentration data obtained by each sensor was plotted, as shown in Fig. 6. The solid line represents the 1:1 correlation line for the slope. Data points closer to this line indicate a better response to the rapidly changing concentrations. The green dashed lines represent ±20% of the 1:1 line. As seen in Fig. 6, all data points are placed above the 1:1 correlation line, meaning that the response time of the low-cost sensors is longer than that for the reference instrument. When the three low-cost sensors were compared, the DC1100 sensors performed the best, followed by the AirBeam2 in terms of the response characteristic. It is concluded that the AirAssure sensors have the lowest performance for the tests at the exponentially decaying particle concentrations. Using the newly introduced test method, it is possible to evaluate the response characteristics of low-cost sensors in unstable environments with rapidly changing particle concentrations.
3.2. Calibration of AirBeam2 and DC1100 Low-cost SensorsFrom the results of the response characteristics of the low-cost sensors, the particle concentrations measured by the AirBeam2 and DC1100 sensors showed exponential decay, even though they have different decay rates compared with those of the reference instrument. The relationship between the particle concentrations of the reference monitor and the AirBeam2 sensors was nonlinear; for the DC1100 sensors, this relationship was almost linear. However, calibration equations based on the reference monitor values in a quadratic form were used for both AirBeam2 and DC1100 for better correction. The corrected (or predicted) particle concentration can be obtained as
where CCLS_raw is the concentration reading before the correction. The regression coefficients are listed in Table S5 in the SM.
Fig. 7 plots particle concentrations (symbols) obtained from each unit of AirBeam2 and DC1100 corrected by using Eq. (4) against the reference readings (Cref). Using these results, linear regression models were obtained, and a summary of the models is shown in Table S6 in the SM. When applying the quadratic correction models, the corrected values of the low-cost sensors under 3- and 6-min concentration decay conditions agree well with reference data, exhibiting a linear relationship with small values of mean absolute error (MAE) and root mean square error (RMSE), which were obtained as follows [28]:
and
As shown in Table S6 in the SM, the maximum MAEs for AirBeam2 and DC1100 under the 3-min concentration decay condition are 3.34 μg/m3 and 155 #/L, respectively. For the 6-min decay case, the estimated maximum MAEs are 2.84 μg/m3 and 229 #/L for these sensors. Moreover, the maximum difference in the slope against the identity line is obtained for unit #3 of the AirBeam2 sensor under the 6-min concentration decay condition (slope: 0.978).
Reproducibility is one of the important features governing the performance of low-cost sensors, which should be examined for calibration. Therefore, the second set of measurement data obtained from each unit of the AirBeam2 and DC1100 sensors was calibrated by employing the regression coefficients estimated from the first measurement data, i.e., the coefficients shown in Table S5 in the SM. The corrected second measurement data are plotted in Fig. S2 in the SM, and the summary of the linear regression models of the corrected data is presented in Table S7 in the SM. For the 6-min concentration decay case (slower concentration decay), the slopes of the linear regression lines approximately range from 0.9 to 1.1 for all three units of AirBeam2 and DC1100. However, poor reproducibility was obtained when the concentration was decaying rapidly in the 3-min concentration decay case. Larger discrepancies were noted for the AirBeam2 sensors, as compared to the DC1100 sensors under this condition. Unit #2 of the AirBeam2 showed a slope of 1.68, which is a significant deviation from the identity line.
4. ConclusionsA new test method was developed for the performance evaluation of low-cost dust sensors. This method employs an exponentially decaying particle concentration in a continuously flowing duct system. Because the exponentially decaying function is mathematically well defined, the test system and test specimen performance can be easily predicted. This method was used to test three different low-cost sensors (AirAssure from TSI Inc., AirBeam2 from HabitatMap LLC, and DC1100 from Dylos). It was found that the response characteristics of the sensors depend on the rate of concentration decay. Moreover, by plotting the slopes of the measurement data and comparing them with the reference instrument, the response characteristics of the sensors could be analyzed quantitatively. In this study, calibration models for each of the AirBeam2 and DC1100 sensors were also introduced. It was found that the reproducibility of the measurement data from the low-cost sensors worsened when the concentration decayed faster. Therefore, for the accurate use of low-cost sensors under rapidly changing concentrations in the real world, more-detailed calibration methods are required. The advantage of the developed test method is that the sensor evaluation time is significantly reduced to less than 10 min. In addition, in the process of manufacturing low-cost sensors, employing the test method and analyzing the findings can provide a detailed and objective assessment of the linearity of sensor response under unsteady particle concentrations.
NotesAuthor Contributions K-T.K. (Ph.D. student) conducted the experiments and wrote the first draft of the manuscript. H.L. (Assistant Professor) analyzed the overall data, wrote the final manuscript, and managed the main revision process. H.O.C. (Researcher) conducted a part of experiments and analysis. K-H.A. (Professor), the corresponding author, planned all experimental procedures and led the overall research and analysis. References1. Holstius DM, Pillarisetti A, Smith KR, Seto E. Field calibrations of a low-cost aerosol sensor at a regulatory monitoring site in California. Atmos Meas Tech. 2014;7:1121–1131.
2. Steinle S, Reis S, Sabel CE, et al. Personal exposure monitoring of PM2.5 in indoor and outdoor microenvironments. Sci Total Environ. 2015;508:383–394.
3. Gao M, Cao J, Seto E. A distributed network of low-cost continuous reading sensors to measure spatiotemporal variations of PM2.5 in Xi’an, China. Environ Pollut. 2015;199:56–65.
4. Kelly KE, Whitaker J, Petty A, et al. Ambient and laboratory evaluation of a low-cost particulate matter sensor. Environ Pollut. 2017;221:491–500.
5. Masiol M, Zíková N, Chalupa DC, Rich DQ, Ferro AR, Hopke PK. Hourly land-use regression models based on low-cost PM monitor data. Environ Res. 2018;167:7–14.
6. Johnson KK, Bergin MH, Russell AG, Hagler GSW. Using low cost sensors to measure ambient particulate matter concentrations and on-road emissions factors. Atmos Meas Tech Discuss. 2016;1–22.
7. Jayaratne R, Liu X, Thai P, Dunbabin M, Morawska L. The influence of humidity on the performance of a low-cost air particle mass sensor and the effect of atmospheric fog. Atmos Meas Tech Tech. 2018;11:4883–4890.
8. Unites States Environmental Protection Agency. Spatial and temporal trends of air pollutants in the south coast basin using low cost sensors. EPA/600/R-17/463. Washington, DC: 2018.
9. Rai AC, Kumar P, Pilla F, et al. End-user perspective of low-cost sensors for outdoor air pollution monitoring. Sci Total Environ. 2017;607–608:691–705.
10. Kuula J, Kuuluvainen H, Rönkkö T, et al. Applicability of optical and diffusion charging-based particulate matter sensors to urban air quality measurements. Aerosol Air Qual Res. 2019;19:1024–1039.
11. Curto A, Donaire-Gonzalez D, Barrera-Gómez J, et al. Performance of low-cost monitors to assess household air pollution. Environ Res. 2018;163:53–63.
12. Li J, Li H, Ma Y, et al. Spatiotemporal distribution of indoor particulate matter concentration with a low-cost sensor network. Build Environ. 2018;127:138–147.
13. Vercellino RJ, Sleeth DK, Handy RG, Min KT, Collingwood SC. Laboratory evaluation of a low-cost, real-time, aerosol multi-sensor. J Occup Environ Hyg. 2018;15:559–567.
14. Thomas GW, Sousan S, Tatum M, et al. Low-cost, distributed environmental monitors for factory worker health. Sensors (Switzerland). 2018;18:1–17.
15. Sousan S, Koehler K, Thomas G, et al. Inter-comparison of low-cost sensors for measuring the mass concentration of occupational aerosols. Aerosol Sci Technol. 2016;50:462–473.
16. Mendoza JA, Lee DH, Kang JH. Photocatalytic removal of NOx using TiO2-coated zeolite. Environ Eng Res. 2016;21:291–296.
17. Morawska L, Thai PK, Liu X, et al. Applications of low-cost sensing technologies for air quality monitoring and exposure assessment: How far have they gone? Environ Int. 2018;116:286–299.
18. Li J, Biswas P. Optical characterization studies of a low-cost particle sensor. Aerosol Air Qual Res. 2017;17:1691–1704.
19. Liu Y, Corey J, Yermakov MV, Wu B, Grinshpun SA. Preliminary development of a real-time respirator seal integrity monitor with low-cost particle sensor. IEEE Trans Ind Appl. 2018;54:3928–3933.
20. Austin E, Novosselov I, Seto E, Yost MG. Laboratory evaluation of the Shinyei PPD42NS low-cost particulate matter sensor. PLoS One. 2015;10:1–17.
21. Polidori A, Quality V, Papapostolou SD, Zhang H. Laboratory evaluation of low-cost air quality sensors laboratory setup and testing protocol. California: South Coast AQMD; Air Quality Sensor Performance Evaluation Center; 2016.
22. Wang Y, Li J, Jing H, Zhang Q, Jiang J, Biswas P. Laboratory evaluation and calibration of three low-cost particle sensors for particulate matter measurement. Aerosol Sci Technol. 2015;49:1063–1077.
23. Ahn KH, Kim SM, Jung HJ, et al. Combined use of optical and electron microscopic techniques for the measurement of hygroscopic property, chemical composition, and morphology of individual aerosol particles. Anal Chem. 2010;82:7999–8009.
24. Malings C, Tanzer R, Hauryliuk A, et al. Fine particle mass monitoring with low-cost sensors: Corrections and long-term performance evaluation. Aerosol Sci Technol. 2020;54:160–174.
25. Williams R, Duvall R, Kilaru V, et al. Deliberating performance targets workshop: Potential paths for emerging PM2.5 and O3 air sensor progress. Atmos Environ X. 2019;2:100031.
26. Austin E, Novosselov I, Seto E, Yost MG. Laboratory evaluation of the Shinyei PPD42NS low-cost particulate matter sensor. PLoS One. 2015;10:1–17.
Fig. 1(a) Schematic of the low-cost dust sensor test setup and (b) mass balance in the particle mixing chamber. 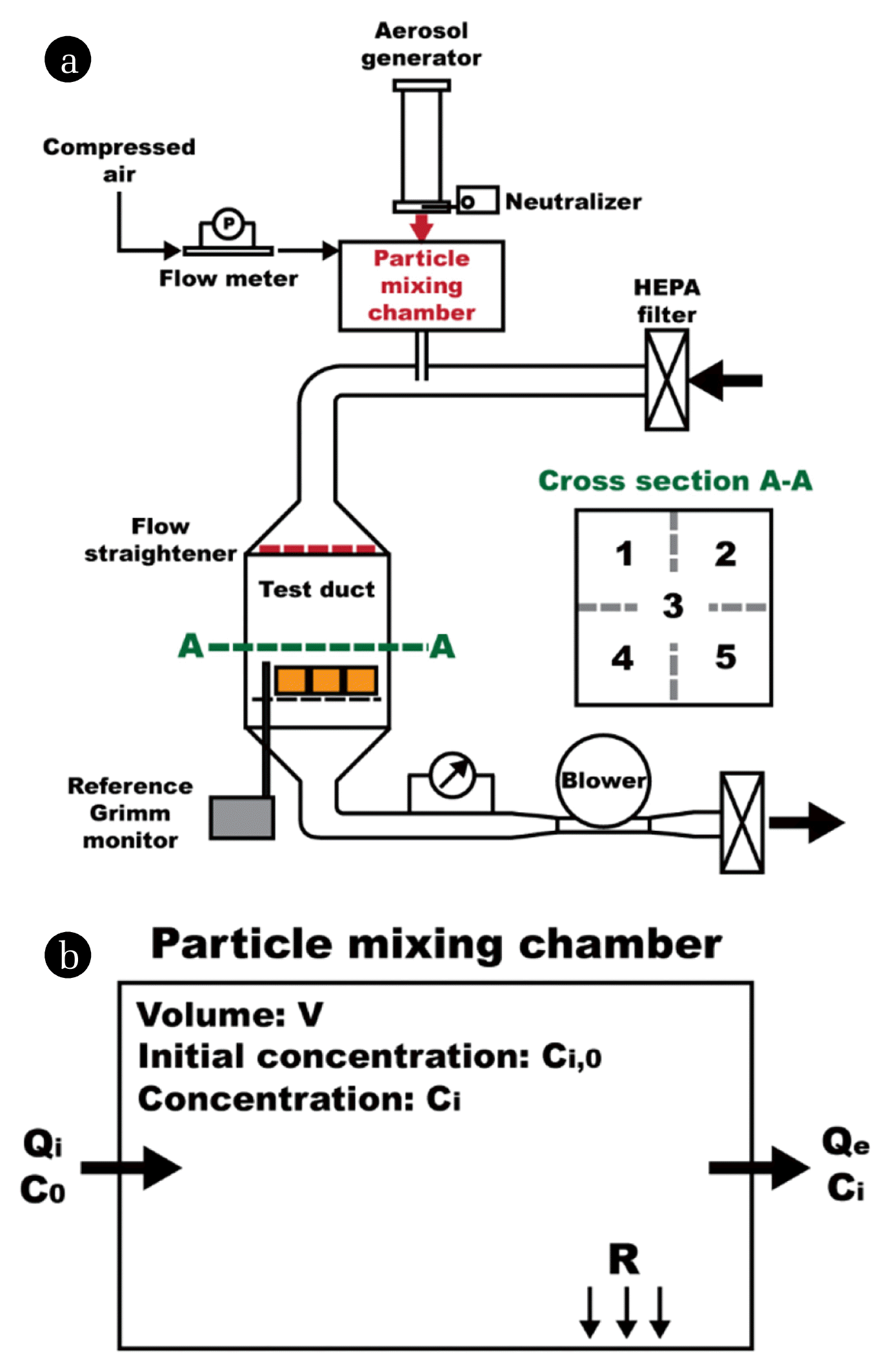
Fig. 2(a) Particle size distributions as a function of elapsed time and (b) PM2.5 mass concentration measured by the Grimm EDM 180 (reference instrument) at the test section. 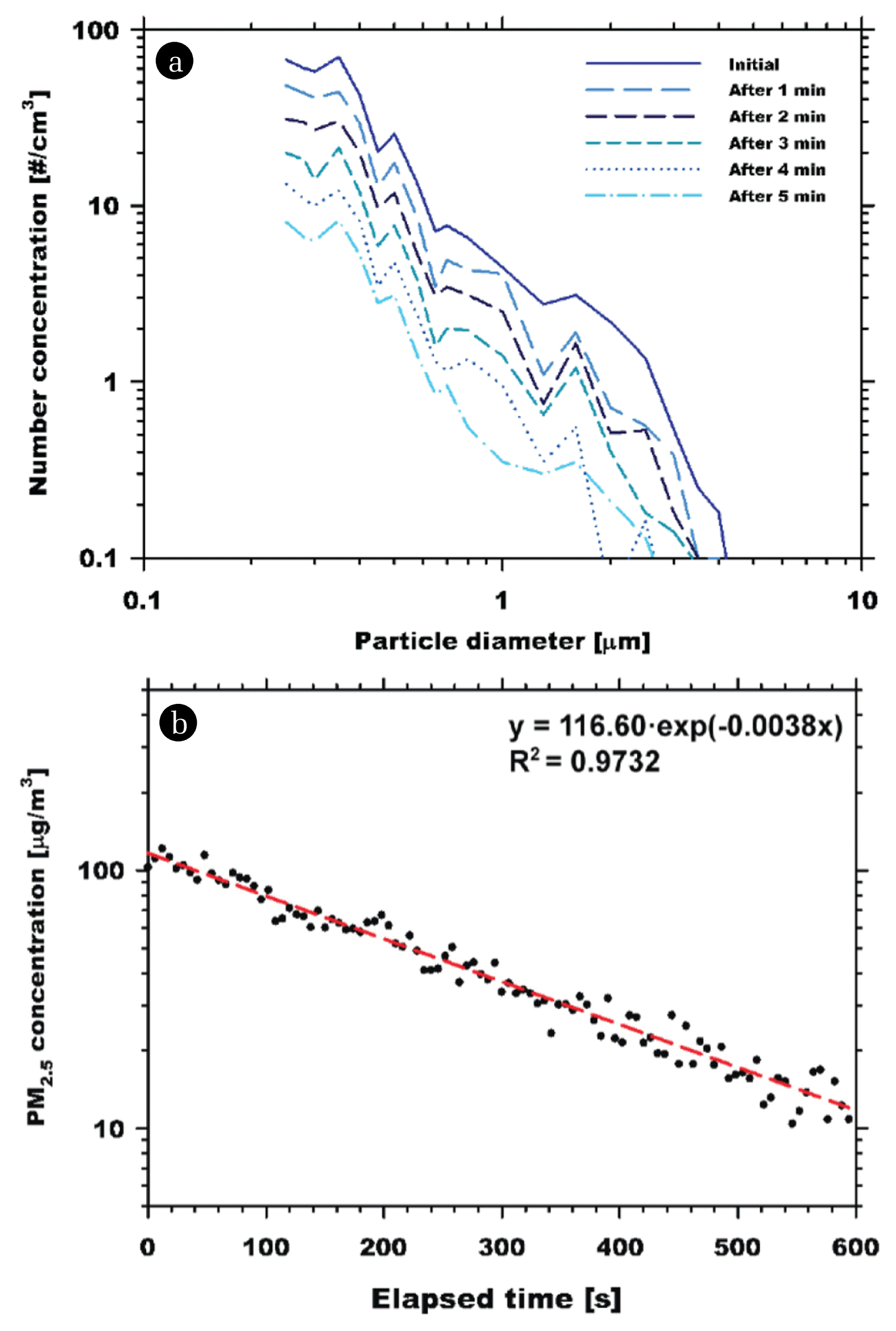
Fig. 3PM2.5 mass concentrations measured by unit #1 of the AirBeam2 under the (a) 3-min and (b) 6-min concentration decay conditions: blue circles represent the data obtained by the reference instrument. 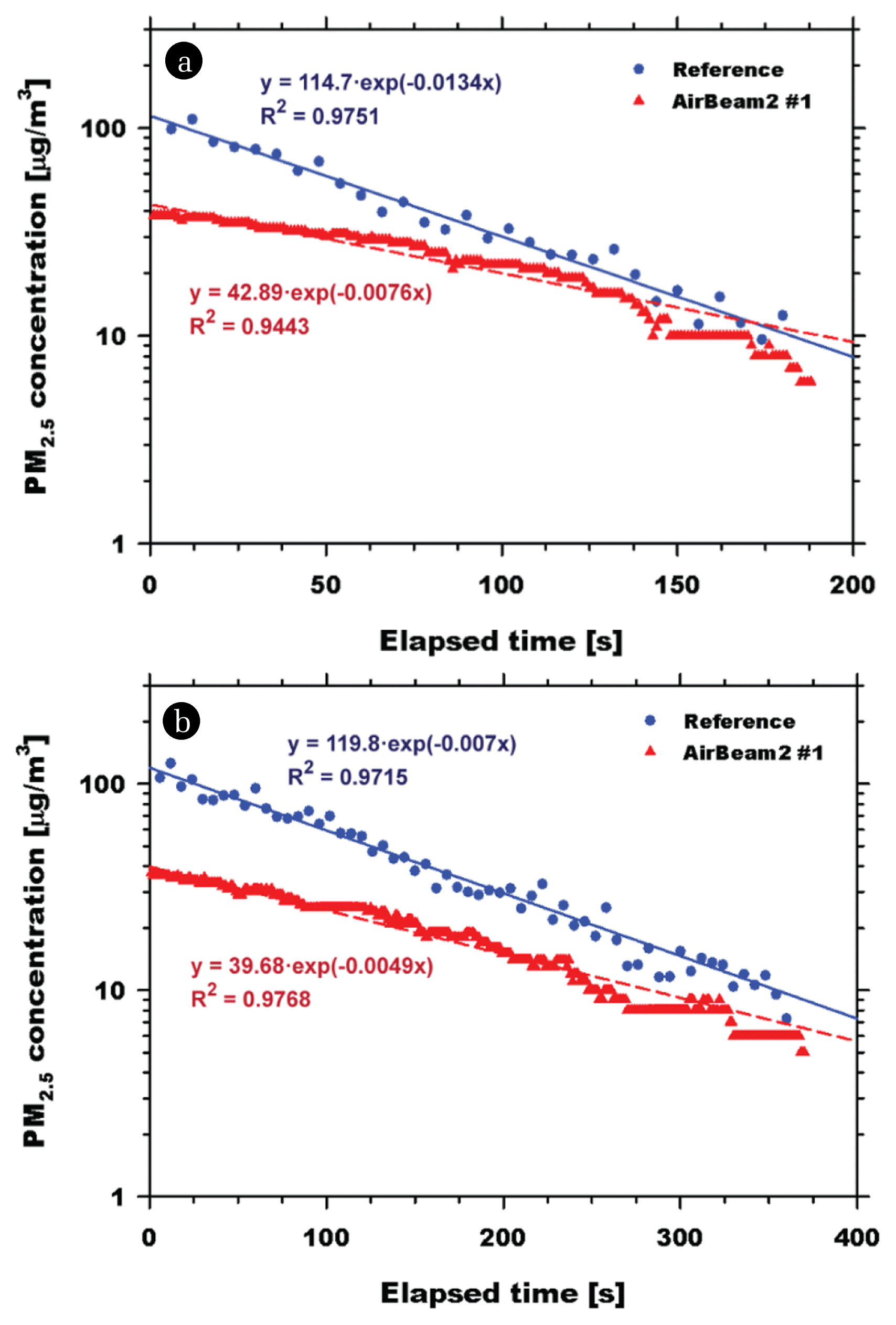
Fig. 4Number concentrations of particles larger than 1 μm measured by unit #1 of the DC1100 under the (a) 3-min and (b) 6-min concentration decay conditions: blue circles represent the data obtained by the reference instrument. 
Fig. 5PM2.5 mass concentrations measured by unit #1 of the AirAssure under the 6-min concentration decay condition: blue circles represent the data obtained by the reference instrument. 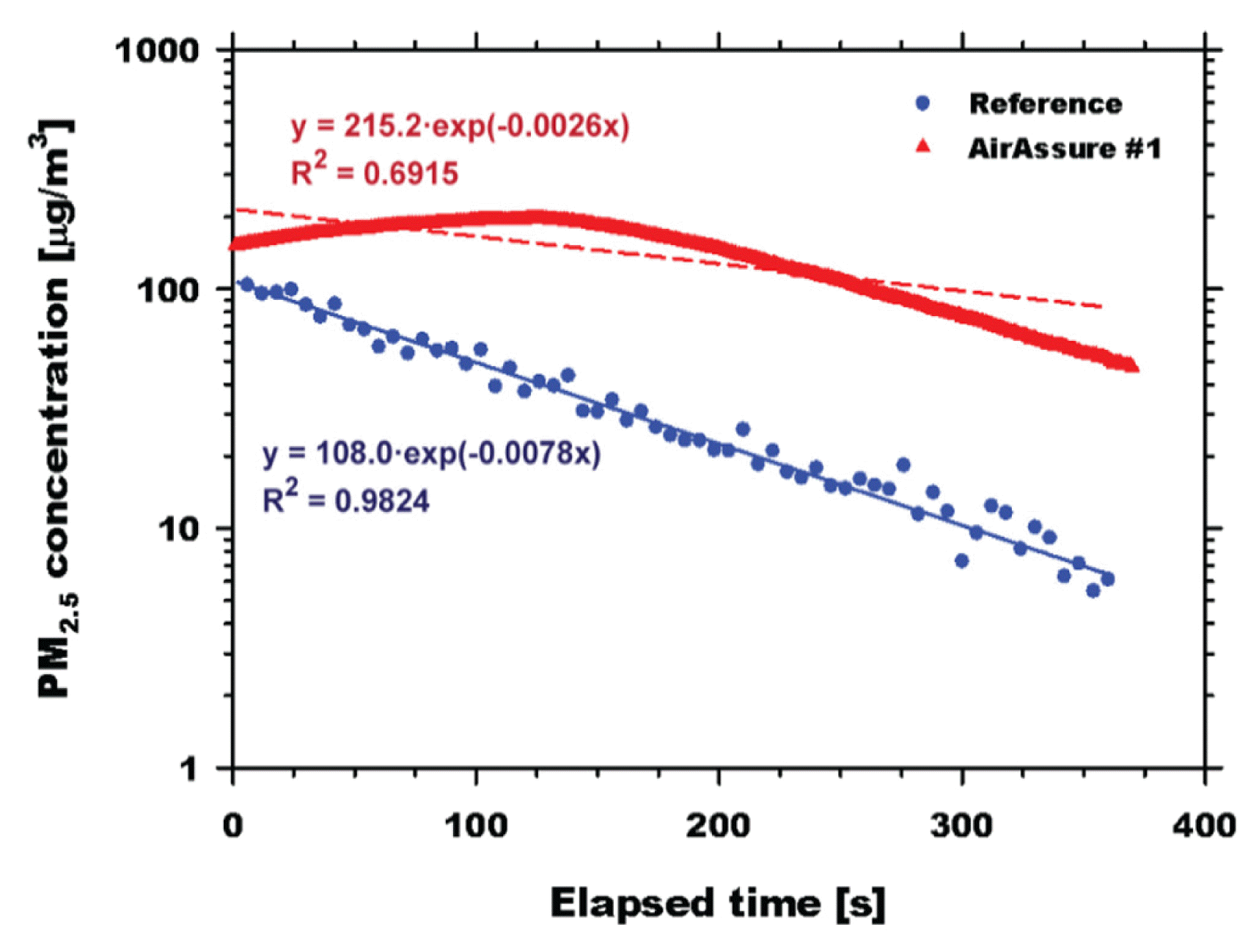
|
|
||||||||||||||||||||||||||||||||||||